湖北省鄂州市2021届九年级上学期数学期末考试试卷

试卷更新日期：2021-04-02 类型：期末考试

进入出卷网下载

一、单选题

1. 下列方程中是一元二次方程的是（）

A、 $x y + 2 = 1$ B、 $y^{2} + \frac{1}{2 y} + 9 = 0$ C、 $x^{2} = 0$ D、 $x^{2} + y^{2} = 1$

查看试题解析
2. 用配方法解方程 $x^{2} - 8 x + 11 = 0$ 的过程中，配方正确的是（）

A、 $x^{2} - 8 x + {(- 4)}^{2} = 5$ B、 $x^{2} - 8 x + {(- 4)}^{2} = 31$ C、 ${(x + 4)}^{2} = 5$ D、 ${(x - 4)}^{2} = - 11$

查看试题解析
3. 一元二次方程 $2 x^{2} + 4 x + 1 = 0$ 的两根为 $x_{1}$ 、 $x_{2}$ ，则 $x_{1} + x_{2}$ 的值是（）

A、 $4$ B、 $- 4$ C、 $- 2$ D、 $2$

查看试题解析
4. 如图，在⊙O中， $\overset{⌢}{A B} = \overset{⌢}{A C}$ ， $∠ B A C = 70 °$ ，则 $∠ A E C$ 的度数是（）

A、 $65 °$ B、 $75 °$ C、 $50 °$ D、 $55 °$

查看试题解析
5. 把抛物线 $y = 2 {(x - 1)}^{2} + 3$ 向上平移 $1$ 个单位，向右平移 $3$ 个单位，得到的抛物线是（）

A、 $y = 2 {(x + 2)}^{2} + 4$ B、 $y = 2 {(x - 4)}^{2} + 4$ C、 $y = 2 {(x + 2)}^{2} + 2$ D、 $y = 2 {(x - 4)}^{2} + 2$

查看试题解析
6. 若圆锥的底面半径为 $2 c m$ ，侧面展开图的面积为 $2 π c m^{2}$ ，则圆锥的母线长为（）

A、 $1 c m$ B、 $2 c m$ C、 $3 c m$ D、 $\frac{π}{2} c m$

查看试题解析
7. 新冠肺炎传染性很强，曾有 $2$ 人同时患上新冠肺炎，在一天内一人平均能传染 $x$ 人，经过两天传染后 $128$ 人患上新冠肺炎，则 $x$ 的值为（）

A、 $10$ B、 $9$ C、 $8$ D、 $7$

查看试题解析
8. 如图，在Rt△ABC中，∠ACB=90°，∠A=60°，AC=6，将△ABC绕点C按逆时针方向旋转得到△A'B'C'，此时点A'恰好在AB边上，则点B'与点B之间的距离为（）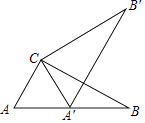

A、12 B、6 C、6 $\sqrt{2}$ D、 $6 \sqrt{3}$

查看试题解析
9. 如图，在△ABC中，AB=10，AC=8，BC=6，以边AB的中点O为圆心，作半圆与AC相切，点P，Q分别是边BC和半圆上的动点，连接PQ，则PQ长的最大值与最小值的和是（）

A、9 B、10 C、 $2 \sqrt{13} + 1$ D、 $\frac{32}{3}$

查看试题解析
10. 二次函数y=ax²+bx+c（a≠0）的部分图象如图所示，图象过点（-1，0），对称轴为直线x=2，下列结论：（1）4a+b=0；（2）9a+c＞3b；（3）8a+7b+2c＞0；（4）若点A（-3，y₁）、点B（- $\frac{1}{2}$ ，y₂）、点C（ $\frac{7}{2}$ ，y₃）在该函数图象上，则y₁＜y₃＜y₂；（5）若方程a（x+1）（x-5）=-3的两根为x₁和x₂ ，且x₁＜x₂ ，则x₁＜-1＜5＜x₂ ．其中正确的结论有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

11. 已知方程 $x^{2} - 4 x + k = 0$ 的一个根是 $x_{1} = - 1$ ，则方程的另一根 $x_{2} =$ .

查看试题解析
12. 顶点为 $(3, 1)$ ，形状与函数 $y = \frac{1}{3} x^{2}$ 的图象相同且开口方向相反的抛物线解析式为.

查看试题解析
13. 如图， $P A$ ， $P B$ 分别与⊙O相切于 $A$ 、 $B$ 两点，点 $C$ 为⊙O上一点，连接 $A C$ 、 $B C$ ，若 $∠ P = 50 °$ ，则 $∠ A C B$ 的度数为.

查看试题解析
14. 如图（a），有一张矩形纸片ABCD，其中AD=6cm，以AD为直径的半圆，正好与对边BC相切，将矩形纸片ABCD沿DE折叠，使点A落在BC上，如图（b）.则半圆还露在外面的部分（阴影部分）的面积为.

查看试题解析
15. $△ A B C$ 中， $∠ B A C = 75 °$ ， $A B = 6$ ， $A C = 4 \sqrt{2}$ ， $P$ 为 $△ A B C$ 内一个动点，则 $P A + P B + P C$ 的最小值为.

查看试题解析
16. 已知函数 $y = b$ 的图象与函数 $y = x^{2} - 3 | x - 1 | - 4 x - 3$ 的图象恰好有四个交点，则 $b$ 的取值范围是.

查看试题解析

三、解答题

17. 用适当的方法解下列方程.

(1)、 $x^{2} - 5 x - 6 = 0$

(2)、 $2 x^{2} + 3 x - 1 = 0$

查看试题解析
18. 如图，在边长为 $1$ 的正方形组成的网格中， $△ A O B$ 的顶点均在格点上，点 $A$ 、 $B$ 的坐标分别是 $A (1 ， 3)$ 、 $B (3 ， 2)$ ，将 $△ A O B$ 绕点 $O$ 逆时针旋转 $90 °$ 后得到 $△ A_{1} O B_{1}$ .（直接填写答案）

(1)、点 $A$ 关于点 $O$ 中心对称的点的坐标为；

(2)、点 $B_{1}$ 的坐标为；

(3)、在旋转过程中，点 $B$ 运动的路径为弧 $\overset{⌢}{B B_{1}}$ ，那么弧 $\overset{⌢}{B B_{1}}$ 的长为.

查看试题解析
19. 为加强素质教育，某学校自主开设了 $A$ 书法、 $B$ 阅读、 $C$ 足球、 $D$ 器乐四门选修课程供学生选择，每门课程被选到的机会均等.

(1)、学生小明计划选修两门课程，请写出所有可能的选法；（用树状图或列表法表示选法）

(2)、若学生小明和小刚各计划选修一门课程，则他们两人恰好同时选修书法或足球的概率是多少？

查看试题解析
20. 已知关于 $x$ 的一元二次方程 $x^{2} + (2 m + 1) x + m^{2} = 0$ 有两个实数根 $x_{1}$ 和 $x_{2}$ .

(1)、求实数 $m$ 的取值范围；

(2)、当 $x_{1}^{2} - x_{2}^{2} = 0$ 时，求 $m$ 的值.

查看试题解析
21. 如图， $C D$ 为⊙O的直径， $C D ⊥ A B$ ，垂足为点 $F$ ， $A O ⊥ B C$ ，垂足为点 $E$ ， $B C = 3$ .

(1)、求 $A B$ 的长；

(2)、求⊙O的半径.

查看试题解析
22. 根据对某市相关的市场物价调研，预计进入夏季后的某一段时间，某批发市场内的甲种蔬菜的销售利润 $y_{1}$ （千元）与进货量 $x$ （吨）之间的函数 $y_{1} = k x$ 的图象如图①所示，乙种蔬菜的销售利润 $y_{2}$ （千元）与进货量 $x$ （吨）之间的函数 $y_{2} = a x^{2} + b x$ 的图象如图②所示.

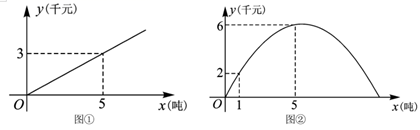(1)、分别求出 $y_{1}$ 、 $y_{2}$ 与 $x$ 之间的函数关系式；

(2)、如果该市场准备进甲、乙两种蔬菜共 $10$ 吨，设乙种蔬菜的进货量为 $t$ 吨.
①写出这两种蔬菜所获得的销售利润之和 $W$ （千元）与 $t$ （吨）之间的函数关系式.并求当这两种蔬菜各进多少吨时获得的销售利润之和最大，最大利润是多少元？

②为了获得两种蔬菜的利润之和不少于 $8400$ 元，则乙种蔬菜进货量应在什么范围内合适？

查看试题解析
23. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ，点 $O$ 在边 $A C$ 上，以 $O A$ 为半径的⊙O交 $A B$ 于点 $D$ ， $B D$ 的垂直平分线交 $B C$ 于点 $E$ ，交 $B D$ 于点 $F$ ，连接 $D E$ .

(1)、判断直线 $D E$ 与⊙O的位置关系，并说明理由；

(2)、若 $A C = 3$ ， $B C = 4$ ， $O A = 1$ ，求线段 $D E$ 的长.

查看试题解析
24. 如图 $1$ ，抛物线 $y = - x^{2} + b x + c$ 与 $x$ 轴交于 $A$ 、 $B$ 两点，与 $y$ 轴交于点 $C$ ，已知点 $B$ 坐标为 $(2 ， 0)$ ，点 $C$ 坐标为 $(0 ， 2)$ .

(1)、求抛物线的表达式；

(2)、如图 $2$ ，点 $P$ 为直线 $B C$ 上方抛物线上的一个动点，当 $△ P B C$ 的面积最大时，求点 $P$ 的坐标；

(3)、如图 $3$ ，过点 $M (1 ， 3)$ 作直线 $M D ⊥ x$ 轴于点 $D$ ，在直线 $M D$ 上是否存在点 $N$ ，使点 $N$ 到直线 $M C$ 的距离等于点 $N$ 到点 $A$ 的距离？若存在，求出点 $N$ 的坐标；若不存在，请说明理由.

查看试题解析