河南省郑州市巩义市2021届九年级上学期数学期末考试试卷

试卷更新日期：2021-04-02 类型：期末考试

进入出卷网下载

一、单选题

1. 下列事件中，属于随机事件的是（）

A、掷一枚硬币10次，仅有1次正面朝上 B、三角形的三个内角之和等于 $180 °$ C、从装有5个红球的袋子里摸出一个白球 D、在地面向上抛出一个篮球还会下落

查看试题解析
2. 一元二次方程 $x^{2} = x$ 的实数根是（）

A、0或1 B、0 C、1 D、±1

查看试题解析
3. 下列函数中，当x＞0时，y随x的增大而增大的是（）

A、 $y = - x + 1$ B、 $y = x^{2} - 1$ C、 $y = \frac{1}{x}$ D、 $y = - x^{2} + 1$

查看试题解析
4. 如图，AB是 $⊙ O$ 的直径，点C，D是圆上两点，且 $∠ C D B$ ＝28°，则 $∠ A O C$ ＝（）

A、56° B、118° C、124° D、152°

查看试题解析
5. 如图，在三角形纸片中， $∠ A = 80 °$ ， $A B = 6$ ， $A C = 8$ .将 $△ A B C$ 沿图示中的虚线剪开，剪下的阴影三角形与原三角形相似的有（）

A、①②③ B、①②④ C、①③④ D、①②③④

查看试题解析
6. 天虹商场一月份鞋帽专柜的营业额为100万元，三月份鞋帽专柜的营业额为150万元.设一到三月每月平均增长率为x，则下列方程正确的是（）

A、100（1+2x）＝150 B、100（1+x）²＝150 C、100（1+x）+100（1+x）²＝150 D、100+100（1+x）+100（1+x）²＝150

查看试题解析
7. 如图， $Δ A B C$ 中 $∠ B A C = 100 °$ ，将 $Δ A B C$ 绕点 $A$ 逆时针旋转 $150 °$ ，得到 $Δ A D E$ ，这时点B、C、D恰好在同一直线上，则 $∠ E$ 的度数为（）

A、 $50^{\circ}$ B、 $75^{\circ}$ C、 $65^{\circ}$ D、 $60^{\circ}$

查看试题解析
8. 如图，在平面直角坐标中，正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形，且相似比为 $\frac{1}{3}$ ，点A ， B ， E在x轴上，若正方形BEFG的边长为12，则C点坐标为（）

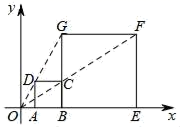A、（6，4） B、（6，2） C、（4，4） D、（8，4）

查看试题解析
9. 如图，平行于x轴的直线与函数y＝ $\frac{k_{1}}{x}$ （k₁＞0，x＞0），y＝ $\frac{k_{2}}{x}$ （k₂＞0，x＞0）的图象分别相交于A，B两点，点A在点B的右侧，C为x轴上的一个动点，若△ABC的面积为6，则k₁﹣k₂的值为（　　）

A、12 B、﹣12 C、6 D、﹣6

查看试题解析
10. 在平面直角坐标系中，若干个半径为1个单位长度、圆心角为 $60 °$ 的扇形组成一条连续的曲线，点 $P$ 从原点 $O$ 出发，向右沿这条曲线做上下起伏运动（如图），点 $P$ 在直线上运动的速度为每秒1个单位长度，点 $P$ 在弧线上运动的速度为每秒 $\frac{π}{3}$ 个单位长度，则2021秒时，点 $P$ 的坐标是（）

A、 $(2021 ， \sqrt{3})$ B、 $(2021 ， - \sqrt{3})$ C、 $(\frac{2021}{2} ， \frac{\sqrt{3}}{2})$ D、 $(\frac{2021}{2} ， - \frac{\sqrt{3}}{2})$

查看试题解析

二、填空题

11. 若关于x的一元二次方程（m﹣2）x²+x+m²﹣4＝0的一个根为0，则m值是．

查看试题解析
12. 如图，在平面直角坐标系 $x o y$ 中，点A的坐标为 $(0 ， 3)$ ，点 $B$ 的坐标为 $(2 ， 1)$ ，点 $C$ 的坐标为 $(2 ， - 3)$ .经画图操作可知 $△ A B C$ 的外心坐标可能是

查看试题解析
13. 将二次函数 $y = x^{2} - 4 x - 4$ 的图象先向上平移3个单位长度，再向右平移2个单位长度得到的图象对应的二次函数的解析式为 $y = x^{2} + a x + b$ ，则 $a b =$ .

查看试题解析
14. 如图，菱形 $A B C D$ 中， $E F ⊥ A C$ ，垂足为点 $H$ ，分别与 $A D$ 、 $A B$ 及 $C B$ 的延长线交于点 $E$ 、 $M$ 、 $F$ ，且 $A E ： F B = 1 ： 2$ ，则 $A H ： A C$ 的值为.

查看试题解析
15. 如图所示，在扇形 $O A B$ 中， $∠ A O B = 90 °$ ，半径 $O A = 4$ ，点 $F$ 位于 $\overset{⌢}{A B}$ 的 $\frac{1}{3}$ 处且靠近点 $A$ 的位置.点 $C$ 、 $D$ 分别在线段 $O A$ 、 $O B$ 上， $C D = 4$ ， $E$ 为 $C D$ 的中点，连接 $E F$ 、 $B E$ .在 $C D$ 滑动过程中（ $C D$ 长度始终保持不变），当 $E F$ 取最小值时，阴影部分的周长为.

查看试题解析

三、解答题

16. 已知关于 $x$ 的方程 $x^{2} - 2 (k + 1) x + k^{2} = 0$ .

(1)、当 $k$ 取何值时，原方程没有实数根？

(2)、对 $k$ 选取一个合适的非零整数，使原方程有两个不相等的实数根，并求此时这两个实数根.

查看试题解析
17. 如图，在直角坐标系中，A(0，4)、C(3，0)，

(1)、①画出线段AC关于y轴对称线段AB；
②将线段CA绕点C顺时针旋转一个角，得到对应线段CD，使得AD∥x轴，请画出线段CD；

(2)、若直线y＝kx平分(1)中四边形ABCD的面积，请直接写出实数k的值.

查看试题解析
18. 图1是一枚质地均匀的正四面体形状的骰子，每个面上分别标有数字2，3，4，5.图2是一个正六边形棋盘，现通过掷骰子的方式玩跳棋游戏，规则是：将这枚骰子在桌面掷出后，看骰子落在桌面上（即底面）的数字是几，就从图中的 $A$ 点开始沿着顺时针方向连续跳动几个顶点，第二次从第一次的终点处开始，按第一次的方法继续……

(1)、随机掷一次骰子，则棋子跳动到点 $C$ 处的概率是.

(2)、随机掷两次骰子，用画树状图或列表的方法，求棋子最终跳动到点 $C$ 处的概率.

查看试题解析
19. 如图，一次函数 $y = k x + b$ 与反比例函数 $y = \frac{6}{x}$ （ $x > 0$ ）的图象交于 $A (m ， 6)$ ， $B (n ， 3)$ 两点.

(1)、求一次函数的解析式；

(2)、根据图象直接写出 $k x + b - \frac{6}{x} < 0$ 时 $x$ 的取值范围；

(3)、若 $M$ 是 $x$ 轴上一点，且 $△ M O B$ 和 $△ A O B$ 的面积相等，求点 $M$ 坐标.

查看试题解析
20. 如图，△ABC是⊙O的内接三角形，AB是⊙O的直径，OF⊥AB，交AC于点F，点E在AB的延长线上，射线EM经过点C，且∠ACE+∠AFO=180°.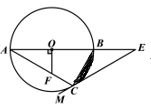

(1)、求证：EM是⊙O的切线；

(2)、若∠A=∠E，BC= $\sqrt{3}$ ，求阴影部分的面积.（结果保留 $π$ 和根号）.

查看试题解析
21. “互联网 $+$ ”时代，网上购物备受消费者青眯，某网店专售一款休闲裤，其成本为每条40元，当售价为每条80元时，每月可售出100条.为了吸引更多顾客，该网店采取降价措施.据市场调查反映：销售单价每降1元，则每月可多销售5条.设每条裤子的售价为 $x$ 元（ $x$ 为正整数），每月的销售量为 $y$ 条.

(1)、直接写出 $y$ 与 $x$ 的函数关系式；

(2)、若销售期间保证销售单价不低于成本单价且每条获利不高 $60 %$ ，设该网店每月获得的利润为 $W$ 元，当销售单价为多少元时，每月获得的利润最大，最大利润是多少？

(3)、在“新冠”疫情期间，全国人民“众志成城，同心抗疫”在销售单价不低于成本单价且每条获利不高于 $60 %$ 的前提下，该网店店主决定每月从利润中捐出1000元用于抗疫.为了保证捐款后每月利润不低于3000元，且让消费者得到最大的实惠，该如何确定休闲裤的销售单价？

查看试题解析
22. 在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $∠ A B C = 30 °$ ，将 $△ A B C$ 绕顶点 $C$ 顺时针旋转，旋转角为 $θ$ （ $0 ° < θ < 180 °$ ），得到 $△ A B^{'} C$ .

(1)、如图①，当 $A B // C B^{'}$ 时，设 $A^{'} B^{'}$ 与 $C B$ 相交于点 $D$ .求证： $△ A^{'} C D$ 是等边三角形.

        图①

(2)、如图②，连接 $A^{'} A$ 、 $B^{'} B$ ，在旋转的过程中， $\frac{A A^{'}}{B B^{'}}$ 的值是否发生变化？如果不变，请求出这个值；如果变化，请说明理由.

       图②

(3)、如图③，设 $A C$ 中点为 $E$ ， $A^{'} B^{'}$ 中点为 $P$ ， $A C = a$ ，连接 $E P$ ，当 $θ =$ $°$ 时， $E P$ 长度最大，最大值为.

        图③

查看试题解析
23. 如图，抛物线 $y = \frac{1}{2} x^{2} + b x + c$ 与x轴交于A、B两点（点A在点B左边），与y轴交于点C.直线 $y = \frac{1}{2} x - 2$ 经过B、C两点.

(1)、求抛物线的解析式；

(2)、点P是抛物线上的一动点，过点P且垂直于x轴的直线与直线 $B C$ 及x轴分别交于点D、M. $P N ⊥ B C$ ，垂足为N.设 $M (m ， 0)$ .
①点P在抛物线上运动，若P、D、M三点中恰有一点是其它两点所连线段的中点（三点重合除外）.请直接写出符合条件的m的值；

②当点P在直线 $B C$ 下方的抛物线上运动时，是否存在一点P，使 $△ P N C$ 与 $△ A O C$ 相似.若存在，求出点P的坐标；若不存在，请说明理由.

查看试题解析