广西壮族自治区玉林市2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-04-02 类型:期末考试
一、单选题
-
1. 计算 的结果是( )A、1 B、-1 C、0 D、-32. 若 ,则 的余角是( )A、25° B、35° C、45° D、125°3. 下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )A、
 赵爽弦图
B、
赵爽弦图
B、 笛卡尔心形线
C、
笛卡尔心形线
C、 科克曲线
D、
科克曲线
D、 斐波那契螺旋线
4. 下列命题中,假命题是( )A、有一个角是直角的菱形是正方形 B、两条对角线相等的菱形是正方形 C、对角线互相垂直的矩形是正方形 D、四条边都相等的四边形是正方形5. 下列计算正确的是( )A、 B、 C、 D、6. 某班抽取6名同学参加体能测试,成绩如下:85,95,85,80,80,85.下列表述错误的是( )
斐波那契螺旋线
4. 下列命题中,假命题是( )A、有一个角是直角的菱形是正方形 B、两条对角线相等的菱形是正方形 C、对角线互相垂直的矩形是正方形 D、四条边都相等的四边形是正方形5. 下列计算正确的是( )A、 B、 C、 D、6. 某班抽取6名同学参加体能测试,成绩如下:85,95,85,80,80,85.下列表述错误的是( )
A、众数是85 B、平均数是85 C、中位数是80 D、极差是157. 在平面直角坐标系中,将函数 的图象向上平移6个单位长度,则平移后的图象与x轴的交点坐标为( )A、(2,0) B、(-2,0) C、(6,0) D、(-6,0)8. 实数a,b,c,d在数轴上的对应点的位置如图所示.若b+d=0,则下列结论正确的是( ) A、b+c 0 B、 1 C、ad bc D、|a| |b|9. 如图,在△ABC中,AB=AC,D是BC的中点,AC的垂直平分线交AC,AD,AB于点E,O,F,则图中全等三角形的对数是( )
A、b+c 0 B、 1 C、ad bc D、|a| |b|9. 如图,在△ABC中,AB=AC,D是BC的中点,AC的垂直平分线交AC,AD,AB于点E,O,F,则图中全等三角形的对数是( )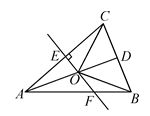 A、1对 B、2对 C、3对 D、4对10. 如图, , 是 的直径, , 是 的弦,且 , 与 交于点 ,连接 , 若 ,则 的度数是( )
A、1对 B、2对 C、3对 D、4对10. 如图, , 是 的直径, , 是 的弦,且 , 与 交于点 ,连接 , 若 ,则 的度数是( )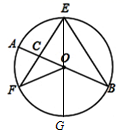 A、20° B、30° C、40° D、50°11. 已知关于x的方式方程 的解是非负数,那么a的取值范围是( )A、a>1 B、a≥1且a≠3 C、a≥1且a≠9 D、a≤112. 二次函数 的部分图象如图所示,图象过点 ,对称轴为直线 ,则有下列结论:① ;② ;③ ;④对于任意实数 , ;其中结论正确的个数为( )
A、20° B、30° C、40° D、50°11. 已知关于x的方式方程 的解是非负数,那么a的取值范围是( )A、a>1 B、a≥1且a≠3 C、a≥1且a≠9 D、a≤112. 二次函数 的部分图象如图所示,图象过点 ,对称轴为直线 ,则有下列结论:① ;② ;③ ;④对于任意实数 , ;其中结论正确的个数为( )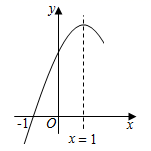 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. ﹣3的相反数是 .14. 分解因式: = .
15. 如图, ,射线CF交AB于E, ,则 的度数为.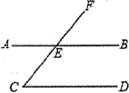 16. 一个不透明的袋子中装有1个白球和3个红球,这些球除颜色外都相同.搅匀后从中任意摸出2个球,摸出两个颜色不同的小球的概率为.17. 如图,在 中, , , ,将 绕点 顺时针旋转,使斜边 过 点,则线段 扫过的面积为.
16. 一个不透明的袋子中装有1个白球和3个红球,这些球除颜色外都相同.搅匀后从中任意摸出2个球,摸出两个颜色不同的小球的概率为.17. 如图,在 中, , , ,将 绕点 顺时针旋转,使斜边 过 点,则线段 扫过的面积为. 18. 杨辉是我国南宋时期杰出的数学家和教育家,如图是杨辉在公元1261年著作《解:九章算法》里面的一张图,即“杨辉三角”.它是古代重要的数学成就,比西方的“帕斯卡三角形”早了300多年.请仔细观察,计算图中第n行中所有数字之和为.
18. 杨辉是我国南宋时期杰出的数学家和教育家,如图是杨辉在公元1261年著作《解:九章算法》里面的一张图,即“杨辉三角”.它是古代重要的数学成就,比西方的“帕斯卡三角形”早了300多年.请仔细观察,计算图中第n行中所有数字之和为.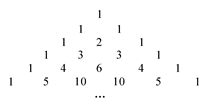
三、解答题
-
19. 计算: .20. 先化简,再求值: ,其中x=2+ .21. 关于 的一元二次方程 有两个不相等的实数根.(1)、求 的取值范围;(2)、当 取满足条件的最大整数时,求方程的根.22. 为了解某校九年级男生200米跑的水平,从中随机抽取部分男生进行测试,并把测试成绩分为 , , , 四个等次绘制成如图所示的不完整的统计图,请你依图解答下列问题:
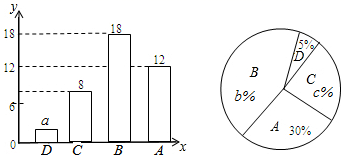 (1)、 ; ; .(2)、扇形统计图中表示C等次的扇形所对的圆心角是;(3)、学校决定从 等次的甲、乙、丙、丁四名男生中,随机选取两名男生参加全市中学生200米跑比赛,请用列表法或画树状图法,求甲、乙两名男生同时被选中的概率.23. 已知,如图,在 中, , 为 边中点.
(1)、 ; ; .(2)、扇形统计图中表示C等次的扇形所对的圆心角是;(3)、学校决定从 等次的甲、乙、丙、丁四名男生中,随机选取两名男生参加全市中学生200米跑比赛,请用列表法或画树状图法,求甲、乙两名男生同时被选中的概率.23. 已知,如图,在 中, , 为 边中点. (1)、尺规作图:以 为直径作 ,交 于点 (保留作图痕迹,不需写作法);(2)、连接 ,求证: 为 的切线.24. 儿童用药的剂量常常按他们的体重来计算,某种药品,体重 的儿童,每次正常服用量为 ;体重 的儿童每次正常服用量为 ;体重在 范围内时,每次正常服用量 是儿童体重 的一次函数中,现实中,该药品每次实际服用量可以比每次正常服用略高一些,但不能超过正常服用量的1.2倍,否则会对儿童的身体造成较大损害.(1)、求y与x之间的函数关系式,并写出自变量x的取值范围;(2)、若该药品的一种包装规格为 /袋,求体重在什么范围的儿童生病时可以一次服下一袋药?25. 如图,矩形 中,点 在边 上,将 沿 折叠,点 落在 边上的点 处,过点 作 交 于点 ,连接 .
(1)、尺规作图:以 为直径作 ,交 于点 (保留作图痕迹,不需写作法);(2)、连接 ,求证: 为 的切线.24. 儿童用药的剂量常常按他们的体重来计算,某种药品,体重 的儿童,每次正常服用量为 ;体重 的儿童每次正常服用量为 ;体重在 范围内时,每次正常服用量 是儿童体重 的一次函数中,现实中,该药品每次实际服用量可以比每次正常服用略高一些,但不能超过正常服用量的1.2倍,否则会对儿童的身体造成较大损害.(1)、求y与x之间的函数关系式,并写出自变量x的取值范围;(2)、若该药品的一种包装规格为 /袋,求体重在什么范围的儿童生病时可以一次服下一袋药?25. 如图,矩形 中,点 在边 上,将 沿 折叠,点 落在 边上的点 处,过点 作 交 于点 ,连接 .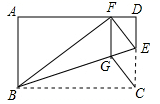 (1)、求证:四边形 是菱形;(2)、若 , ,求 的长.26. 已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(﹣2,0),点P是线段AB上方抛物线上的一个动点.
(1)、求证:四边形 是菱形;(2)、若 , ,求 的长.26. 已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(﹣2,0),点P是线段AB上方抛物线上的一个动点.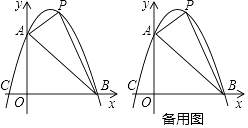 (1)、求抛物线的解析式;
(1)、求抛物线的解析式;
(2)、当点P运动到什么位置时,△PAB的面积有最大值?(3)、过点P作x轴的垂线,交线段AB于点D,再过点P做PE∥x轴交抛物线于点E,连结DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求出点P的坐标;若不存在,说明理由.