广西壮族自治区防城港市2021届九年级上学期数学期末考试试卷
试卷更新日期：2021-04-02 类型：期末考试
一、单选题
-
1. 方程x2＝1的解是（ ）A、x1＝0，x2＝1 B、x1＝0，x2＝﹣1 C、x1＝1，x2＝﹣1 D、x1＝x2＝12. 下列垃圾分类的图标是中心对称图形的是（ ）.A、
厨余垃圾（绿色）
B、
其他垃圾（黑色）
C、
可回收物（蓝色）
D、
有害垃圾（红色）
3. 抛物线y＝（x﹣1）2+3的顶点坐标是（ ）A、（1，3） B、（﹣1，3） C、（1，﹣3） D、（3，﹣1）4. 一个圆锥的底面半径长为4cm，母线长为5cm，则圆锥的侧面积为（ ）A、20cm2 B、40cm2 C、20πcm2 D、40πcm25. 如图，四边形ABCD是⊙O的内接四边形，若∠BOD＝80°，则∠BCD的度数是（ ）
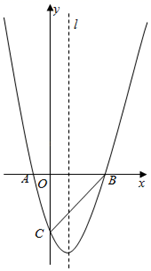
A、80° B、120° C、130° D、140°6. 不透明袋子中有除颜色外完全相同的3个黑球和2个白球，从袋子中随机摸出3个球，下列事件中是必然发生的事件是（ ）A、2个白球1个黑球 B、2个黑球1个白球 C、至少有1个黑球 D、3个都是黑球7. 抛物线y＝ax2+bx+c的部分图象如图所示，对称轴为直线x＝﹣1，则当y＜0，x的取值范围是（ ）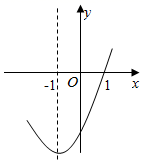
A、x＜1 B、x＞﹣1 C、﹣3＜x＜1 D、﹣4≤x≤18. 已知⊙O的半径是2，一个正方形内接于⊙O，则这个正方形的边长是（ ）A、2 B、2 C、 D、49. 我国南宋数学家杨辉所著《田亩比类乘除算法》有题目：直田积（矩形面积）八百六十四步（平方步），只云阔（宽）与长共六十步，问阔（宽）及长各几步.设阔（宽）有x步，那么下面所列方程正确的是（ ）A、x（x+60）＝864 B、x （60﹣x）＝864 C、x （x﹣60）＝864 D、x2﹣60x﹣864＝010. 如图，△ABC中，∠ACB＝90°，∠ABC＝40°.将△ABC绕点B逆时针旋转得到△A′BC′，使点C的对应点C′恰好落在边AB上，则∠CAA′的度数是（ ）
A、50° B、70° C、110° D、120°11. 如图，正方形ABCD中，分别以A、C为圆心，以正方形的边长2为半径面弧，形成树叶形（阴影部分）图案，则树叶形图案的面积是（ ）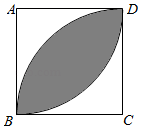
A、2π﹣4 B、4﹣π C、π+4 D、4﹣2π12. 如图，抛物线y＝ax2+bx+c的对称轴是x＝1，下列结论：①abc＞0；②b2﹣4ac＞0； ③8a+c＜0； ④5a+b+2c＞0，正确的是（ ）
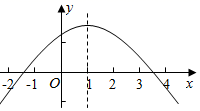A、①②③ B、②③④ C、①②④ D、②③二、填空题
-
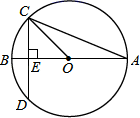
13. 二次函数y＝x2+2x﹣3的图象与y轴的交点坐标是.14. 将一元二次方程2x2＝x﹣1化成一般形式是.15. 将抛物线y＝2x2向左平移2个单位，所得抛物线的对称轴是直线.16. 如图，圆O的直径AB垂直于弦CD，垂足是E，∠A＝22.5°，OC＝4，CD的长为.
17. 有一人患了流感，经过两轮传染后共有100人患了流感，那么每轮传染中，平均一个人传染的人数为.18. 如图，点E在正方形ABCD的边CD上，将△ADE绕点A顺时针旋转90°到△ABF的位置，连接EF，过点A作EF的垂线，垂足为点H，与BC交于点G.若BG＝5，CG＝3，则CE的长为.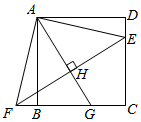
三、解答题
-
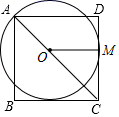
19. 解方程：x2﹣1＝3（x+1）.20. 在圆柱形油槽内装入一些油以后，截面如图.截面圆的直径为200cm，若油面的宽AB＝160cm，求油槽中油的最大深度.
21. 如图，在平面直角坐标系中，△ABC的三个顶点分别是A（﹣2，﹣1），B（﹣4，﹣4），C（﹣1，﹣3）.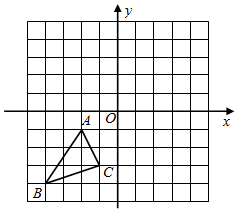
(1)、把△ABC向右平移4个单位后得到对应的△A1B1C1 ， 请画出平移后的△A1B1C1；(2)、把△ABC绕原点O旋转180°后得到对应的△A2B2C2 ， 请画出旋转后的△A2B2C2；(3)、观察图形可知，△A1B1C1与△A2B2C2关于点（ ， ）成中心对称.22. 已知关于x方程x2+ax+a﹣5＝0.(1)、若该方程的一个根为3，求a的值及该方程的另一根；(2)、求证：不论a取何实数，该方程都有两个不相等的实数根.23. 某市合唱团为开展“百人合唱爱国歌”网络“线上云演出”活动，需招收新成员、小霞、小健、小婷、小宇四名学生报名参加了应聘活动，其中小霞、小健来自七年级，小婷、小宇来自八年级.现对这四名学生采取随机抽取的方式进行网络线上面试.(1)、若随机抽取一名学生，恰好抽到学生小霞的概率为；(2)、若随机抽取两名学生，请用列表法或树状图法求抽中两名学生均来自七年级的概率.24. 某商店将标价为100元/台的品牌学习机在网上直播间销售，两次降价后，价格为81元/台，并且两次降价的百分率相同.(1)、求该品牌学习机每次降价的百分率；(2)、从第二次降价后的第1天算起，第x天的销量及网上直播间销售支出劳务费用的相关信息如表所示：时间（天）
x
销量（台）
150﹣x
网上直播间售支出劳务费用（元）
3x2﹣50x+600
已知该品牌学习机的进价为61元/台，设销售该品牌学习机第x（天）的利润为y（元），求y与x之间的函数解析式，并求出第几天时销售利润最大，最大利润是多少？
