广西壮族自治区百色市德保县2021届九年级上学期数学期末考试试卷

试卷更新日期：2021-04-02 类型：期末考试

进入出卷网下载

一、单选题

1. $\tan 45 °$ 的值为（）

A、 $\frac{\sqrt{3}}{3}$ B、 $\frac{\sqrt{3}}{2}$ C、1 D、 $\sqrt{3}$

查看试题解析
2. 抛物线 $y = {(x - 1)}^{2} + 2$ 的顶点坐标是（）

A、（﹣1，2） B、（﹣1，﹣2） C、（1，﹣2） D、（1，2）

查看试题解析
3. 下列图形中，是中心对称图形的为（）

A、 B、 C、 D、

查看试题解析
4. 如图，已知D、E分别为AB、AC上的两点，且DE∥BC，AE＝3CE，AB＝8，则AD的长为（　　）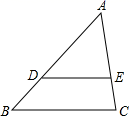

A、3 B、4 C、5 D、6

查看试题解析
5. 反比例函数 $y = \frac{2}{x}$ $(x < 0)$ 的图象位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
6. 已知△ABC∽△DEF ，若△ABC与△DEF的相似比为2：3，△ABC的面积为40，则△DEF的面积为（）

A、60 B、70 C、80 D、90

查看试题解析
7. 如图，一辆小车沿倾斜角为 $α$ 的斜坡向上行驶13m，若 $\sin α = \frac{5}{13}$ ，则小车上升的高度是（）

A、4米 B、5米 C、6米 D、12米

查看试题解析
8. 一根水平放置的圆柱形输水管道横截面如图所示，其中有水部分水面宽0.8米，最深处水深0.2米，则此输水管道的直径是（）

A、1 B、2 C、3 D、4

查看试题解析
9. 如图，AD，BC相交于点O，由下列条件仍不能判定△AOB与△DOC相似的是（）

A、AB∥CD B、∠C＝∠B C、 $\frac{O A}{O D} = \frac{O B}{O C}$ D、 $\frac{O A}{O D} = \frac{A B}{C D}$

查看试题解析
10. 一个面积为 $10$ 的矩形，若长与宽分别为x， y，则y与x之间的关系用图象可大致表示为（）

A、 B、 C、 D、

查看试题解析
11. 如图， $C D$ 是Rt△ $A B C$ 斜边 $A B$ 上的高， $C D = 6$ ， $B D = 4$ ，则 $A B$ 的长为（）

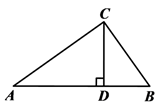A、12 B、13 C、14 D、15

查看试题解析
12. 如图所示，二次函数 $y = a x^{2} + b x + c$ 的图象经过点（－1，2），且与 $x$ 轴交点的横坐标分别为 $x_{1}$ ， $x_{2}$ ，其中 $- 2 < x_{1} < - 1$ ， $0 < x_{2} < 1$ ，下列结论：① $a b c > 0$ ；② $4 a - 2 b + c < 0$ ；③ $2 a - b < 0$ ；④ $b^{2} + 8 a > 4 a c$ .其中正确的有（）

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析

二、填空题

13. 若 $\frac{a}{b} = \frac{8}{5}$ ，则 $\frac{a - b}{b} =$ .

查看试题解析
14. 已知反比例函数 $y = \frac{k}{x}$ 的图象经过点 $(- 3, - 1)$ ，则 $k =$ .

查看试题解析
15. 如图，AB是⊙O的直径，CD是弦，若∠BCD＝36°，则∠ABD的度数为.

查看试题解析
16. 学完《相似三角形》后，数学兴趣小组的同学利用周末来测量学校附近的河宽（如图）， $A E$ 与 $B C$ 相交于点 $D$ ， $∠ B = ∠ C = 90^{\circ}$ ，测得 $B D = 120 m$ ， $D C = 60 m$ ， $E C = 50 m$ ，求得河宽 $A B =$ $m$ .

查看试题解析
17. 如图，用一个半径为30cm扇形铁皮，制作一个无底的圆锥（不计损耗），经测量圆锥的底面半径r为10cm，则扇形铁皮的面积为 cm² .（结果保留π）

查看试题解析
18. 如图，在△ABC中，∠C ＝90°，AB ＝10cm，BC ＝8cm，点P从点A沿AC向点C以1cm/s的速度运动，同时点Q从点C沿CB向点B以2cm/s的速度运动（点Q运动到点B停止），在运动过程中，四边形PABQ的面积最小值为cm²

查看试题解析

三、解答题

19. 计算： $\sqrt{8} + {(- 2021)}^{0} - 4 \sin 45 ° - 2 \cos 30 °$

查看试题解析
20. 已知：△ABC三个顶点的坐标分别为A（－2，－2），B（－5，－4），C（－1，－5）.

（ 1 ）画出△ABC关于x轴对称的△A₁B₁C₁；

（ 2 ）以点O为位似中心，将△ABC放大为原来的2倍，得到△A₂B₂C₂ ，请在网格中画出△A₂B₂C₂ ，并写出点B₂的坐标.

查看试题解析
21. 如图，在△PAB中，点C、D在AB上，PC＝PD＝CD，∠A ＝∠BPD，△APC与△BPD相似吗？为什么？

查看试题解析
22. 如图，AB为⊙O的直径，D为AB延长线上的点，AC为弦，且∠A＝∠D＝30°.

(1)、求证：DC是⊙O的切线；

(2)、若⊙O的半径为1cm，求图中阴影部分的面积.

查看试题解析
23. 在平面直角坐标系 $x O y$ 中，过点 $A (- 4 ， 2)$ 向 $x$ 轴作垂线，垂足为 $B$ ，连接 $A O$ .双曲线 $y = \frac{k}{x}$ 经过斜边 $A O$ 的中点 $C$ ，与边 $A B$ 交于点 $D$ .

(1)、求反比例函数的解析式；

(2)、求△ $B O D$ 的面积.

查看试题解析
24.
如图，埃航MS804客机失事后，国家主席亲自发电进行慰问，埃及政府出动了多艘舰船和飞机进行搜救，其中一艘潜艇在海面下500米的A点处测得俯角为45°的前下方海底有黑匣子信号发出，继续沿原方向直线航行2000米后到达B点，在B处测得俯角为60°的前下方海底有黑匣子信号发出，求海底黑匣子C点距离海面的深度（结果保留根号）．

查看试题解析
25. 如图，AB为⊙O的直径，点C是⊙O上一点，CD与⊙O相切于点C，过点A作AD⊥DC，连接AC，BC.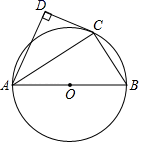

(1)、求证：AC是∠DAB的角平分线；

(2)、若AD＝2，AB＝3，求AC的长.

查看试题解析
26. 如图，抛物线y＝ax²+bx﹣3过A（1，0），B（﹣3，0），直线AD交抛物线于点D ，点D的横坐标为﹣2，点P（m ， n）是线段AD上的动点．

(1)、求直线AD及抛物线的解析式；

(2)、过点P的直线垂直于x轴，交抛物线于点Q ，求线段PQ的长度l与m的关系式，m为何值时，PQ最长？

(3)、在平面内是否存在整点（横、纵坐标都为整数）R ，使得P ， Q ， D ， R为顶点的四边形是平行四边形？若存在，直接写出点R的坐标；若不存在，说明理由．

查看试题解析