广西河池市南丹县2021届九年级上学期数学期末考试试卷

试卷更新日期：2021-04-02 类型：期末考试

进入出卷网下载

一、单选题

1. 下列方程是关于x的一元二次方程的是（）

A、ax²＋bx＋c＝0 B、 $\frac{1}{x^{2}} + x = 1$ C、x²＋2x＝y²－1 D、3（x＋1）²＝2（x＋1）

查看试题解析
2. 关于x的方程 $2 x^{2} - 5 = 3 x$ 的二次项系数和一次项系数分别是（）

A、3， $- 2$ B、3，2 C、2， $- 3$ D、2， $- 5$

查看试题解析
3. 下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 抛物线y＝2x² ， y＝－2x² ， y＝ $\frac{1}{2}$ x²的共同性质是（）

A、开口向上 B、对称轴是y轴 C、都有最高点 D、y随x的增大而增大

查看试题解析
5. 下列事件是必然事件的是（）

A、阴天一定会下雨 B、打开电视机，任选一个频道，屏幕上正在播放新闻联播 C、购买一张体育彩票，中奖 D、任意画一个三角形，其内角和是180°

查看试题解析
6. 已知⊙O的直径为12cm，如果圆心O到一条直线的距离为7cm，那么这条直线与这个圆的位置关系是（）

A、相离 B、相切 C、相交 D、相交或相切

查看试题解析
7. 用配方法解一元二次方程 $x^{2} + 8 x - 3 = 0$ ，下列变形中正确的是（）

A、 ${(x - 4)}^{2} = 19$ B、 ${(x + 4)}^{2} = 19$ C、 ${(x + 8)}^{2} = 61$ D、 ${(x - 8)}^{2} = 67$

查看试题解析
8. 从箱子中摸出红球的概率为 $\frac{1}{4}$ ，已知口袋中红球有 $4$ 个，则袋中共有球（）个

A、 $24$ B、 $16$ C、 $8$ D、 $4$

查看试题解析
9. 如图，AB是⊙O的直径，弦CD⊥AB于点E．若AB=8，AE=1，则弦CD的长是（）

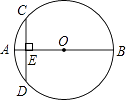A、 $\sqrt{7}$ B、2 $\sqrt{7}$ C、6 D、8

查看试题解析
10. 如图，点D是等腰直角三角形ABC内一点，AB=AC，若将△ABD绕点A逆时针旋转到△ACE的位置，则∠AED的度数为（）

A、25° B、30° C、40° D、45°

查看试题解析
11. 如果一个扇形的弧长等于它的半径，那么此扇形称为“等边扇形”，则半径为2的“等边扇形”的面积为（）

A、Π B、1 C、2 D、 $\frac{2}{3} π$

查看试题解析
12. 如图， $∠ A B C = 70 °$ ， $O$ 为射线 $B C$ 上一点，以点 $O$ 为圆心， $\frac{1}{2} O B$ 长为半径做 $⊙ O$ ，要使射线 $B A$ 与 $⊙ O$ 相切，应将射线绕点 $B$ 按顺时针方向旋转（）

A、40°或100° B、100° C、70° D、40°

查看试题解析

二、填空题

13. 如图，AB是⊙O的直径，BC是⊙O的弦.若∠OBC＝60°，则∠BAC=.

查看试题解析
14. 二次函数 $y = 2 x^{2} + c$ 的图象经过点 $(1, - 4)$ ，则c的值为.

查看试题解析
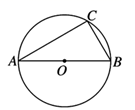15. 在一个不透明的袋子中，装有红球、黄球、篮球、白球各1个，这些球除颜色外无其他差别，从袋中随机取出一个球，取出红球的概率为

查看试题解析
16. 将抛物线 $y = - \frac{1}{3} {(x - 5)}^{2} + 3$ 向左平移5个单位，再向上平移2个单位后得到的抛物线的解析式为.

查看试题解析
17. 某足球比赛，要求每两支球队之间都要比赛一场，若共比赛 $45$ 场，则有支球队参加比赛.

查看试题解析
18. 如图，在平面直角坐标系中，抛物线 $y = \frac{1}{2} x^{2}$ 经过平移得到抛物线 $y = \frac{1}{2} x^{2} - 2 x$ ，其对称轴与两段抛物线所围成的阴影部分的面积是

查看试题解析

三、解答题

19. 解方程： ${(x + 2)}^{2} = 3 (x + 2)$

查看试题解析
20. 如图所示，在平面直角坐标系中三个顶点的坐标分别是点A（﹣2，3），点B（﹣1，1），点C（0，2）.

(1)、作△ABC关于O成中心对称的△A₁B₁C₁；

(2)、将△A₁B₁C₁向右平移4个单位，作出平移后的△A₂B₂C₂；

(3)、在x轴上求作点P，使PA₁＋PC₂的值最小.

查看试题解析
21. 有一个可自由转动的转盘，被分成了4个相同的扇形，分别标有数1，2，3，4（如图所示），另有一个不透明的口袋装有分别标有数0，1，3的三个小球（除数字不同外，其余都相同），小亮转动一次转盘，停止后指针指向某一扇形（指针指向两个扇形的交线时，当作指向右边的扇形），扇形内的数是小亮的幸运数，小红任意摸出一个小球，小球上的数是小红的吉祥数，然后计算这两个数的积.

(1)、请你用画树状图或列表的方法，求这两个数的积为0的概率；

(2)、小亮与小红做游戏，规则是：若这两个数的积为奇数，小亮赢；否则，小红赢.你认为该游戏公平吗？为什么？如果不公平，请你修改该游戏规则，使游戏公平.

查看试题解析
22. 已知关于x的一元二次方程mx²﹣2mx+（m﹣1）＝0.

(1)、若方程的一个根是x＝2，求m的值及另一个根；

(2)、当m＞1时方程有实数根吗？请说明理由.

查看试题解析
23. 如图，在等腰 $△ A B C$ 中，AC＝AB，∠CAB＝90°，E是BC上一点，将E点绕A点逆时针旋转90°到AD，连接DE、CD.

(1)、求证： $△ A B E ≌ △ A C D$ ；

(2)、当BC＝6，CE＝2时，求DE的长.

查看试题解析
24. 如图，在 $Δ A B C$ 中， $A B = A C$ ，以 $A B$ 为直径的 $⊙ O$ 交 $B C$ 于点 $D$ ，交 $A C$ 于点 $E$ ，直线 $D F ⊥ A C$ 于点 $F$ ，交 $A B$ 的延长线于点 $G$ .

(1)、求证： $B D = C D$ .

(2)、求证： $G F$ 是 $⊙ O$ 的切线.

查看试题解析
25. 某商场在去年底以每件80元的进价购进一批同型号的服装，一月份以每件150元的售价销售了320件，二、三月份该服装畅销，销量持续走高，在售价不变的情况下，三月底统计知三月份的销量达到了500件

(1)、求二、三月份服装销售量的平均月增长率

(2)、从四月份起商场因换季清仓采用降价促销的方式，经调查发现，在三月份销量的基础上，该服装售价每降价5元，月销售量增加10件，当每件降价多少元时，四月份可获利12000元?

查看试题解析
26. 如图，已知二次函数 $y = a x^{2} - 4 x + c$ 的图象经过点A（-1，0）和点D（5，0）.

(1)、求该二次函数的解析式；

(2)、直接写出该抛物线的对称轴及顶点C的坐标；

(3)、点B是该抛物线与y轴的交点，求四边形ABCD的面积.

查看试题解析