初中数学人教版八年级下学期期中专题复习 :05 菱形
试卷更新日期:2021-04-02 类型:复习试卷
一、单选题
-
1. 矩形具有而菱形不具有的性质是( )A、对角相等 B、对角线互相垂直 C、对角线相等 D、对边平行2. 已知四边形ABCD是平行四边形,则下列结论中正确的是( )A、当AB⊥BD时,它是菱形 B、当AC=BD时,它是正方形 C、当∠ABC=90°时,它是矩形 D、当AB=BC时,它是矩形3. 如图,菱形ABCD的两条对角线长分别为AC=6,BD=8,点P是BC边上的一动点,则AP的最小值为( )
 A、4 B、4.8 C、5 D、5.54. 如图,菱形 中, ,则 的度数为( )
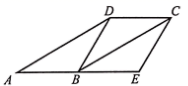
A、4 B、4.8 C、5 D、5.54. 如图,菱形 中, ,则 的度数为( )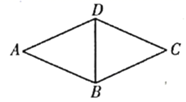 A、 B、 C、 D、5. 如图,在菱形ABCD中, , ,则 的周长等于( )
A、 B、 C、 D、5. 如图,在菱形ABCD中, , ,则 的周长等于( )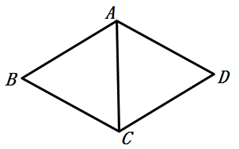 A、20 B、15 C、10 D、126. 已知一个菱形的周长为8,有一个内角为120°,则该菱形较短的对角线长为( )A、4 B、 C、2 D、1
A、20 B、15 C、10 D、126. 已知一个菱形的周长为8,有一个内角为120°,则该菱形较短的对角线长为( )A、4 B、 C、2 D、1二、填空题
-
7. 如图,在四边形 中,对角线 交于点 ,且 ,若要使四边形 是菱形,则可以添加的条件是 .
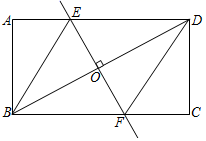
 8. 如图,AC是菱形ABCD的对角线,P是AC上的一个动点,过点P分别作AB和BC的垂线,垂足分别是点F和E,若菱形的周长是12cm,面积是6cm2 , 则PE+PF的值是cm.
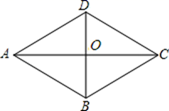
8. 如图,AC是菱形ABCD的对角线,P是AC上的一个动点,过点P分别作AB和BC的垂线,垂足分别是点F和E,若菱形的周长是12cm,面积是6cm2 , 则PE+PF的值是cm. 9. 如图,已知菱形ABCD中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形的面积是 .
9. 如图,已知菱形ABCD中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形的面积是 .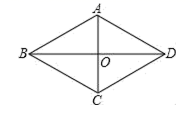 10. 如图,菱形ABCD的边长为13,对角线AC=24,点E、F分别是边CD、BC的中点,连接EF 并延长与AB的延长线相交于点G,则EG = .
10. 如图,菱形ABCD的边长为13,对角线AC=24,点E、F分别是边CD、BC的中点,连接EF 并延长与AB的延长线相交于点G,则EG = .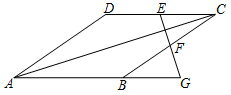
三、综合题