2015-2016学年湖南省衡阳市衡阳县高二上学期期末数学试卷（理科）

试卷更新日期：2016-07-25 类型：期末考试

进入出卷网下载

一、单选题

1. 设a，b，c∈R，且a＞b，则（　　）

A、ac＞bc B、 $a^{2} > b^{2}$ C、 $a^{3} > b^{3}$ D、 $\frac{1}{a}$ ＜ $\frac{1}{b}$

查看试题解析
2. 设命题p：∃n∈N，n²＞2n，则￢p为（　　）

A、∀n∈N， $n^{2}$ ≤2n B、∃n∈N， $n^{2}$ ＜2n C、∃n∈N， $n^{2}$ ≤2n D、∀n∈N， $n^{2}$ ＜2n

查看试题解析
3. 等比数列{a_n}中，已知a₂=3，a₇•a₁₀=36，则a₁₅等于（　　）

A、12 B、-12 C、6 D、-6

查看试题解析
4. 在△ABC中，角A，B，C所对的边分别为a，b，c．若a=3，b=2，cos（A+B）= $\frac{1}{3}$ ，则c=（　　）

A、4 B、 $\sqrt{15}$ C、3 D、 $\sqrt{17}$

查看试题解析
5. 若 $\{\begin{matrix} x - y \leq 0 \\ x + y \leq 1 \\ x \geq 0 \end{matrix}$ ，则z=x+2y的最小值为（　　）

A、-1 B、0 C、 $\frac{3}{2}$ D、2

查看试题解析
6. 若直线 $\frac{x}{a} + \frac{y}{b}$ =1（a＞0，b＞0）过点（1，1），则a+b的最小值等于（　　）

A、2 B、3 C、4 D、5

查看试题解析
7. 已知抛物线y²=2px（p＞0）的准线经过点（﹣1，1），则该抛物线焦点坐标为（　　）

A、（﹣1，0） B、（1，0） C、（0，﹣1） D、（0，1）

查看试题解析
8. 下列双曲线中，焦点在y轴上且渐近线方程为y=± $\frac{1}{2}$ x的是（　　）

A、 $x^{2}$ ﹣ $\frac{y^{2}}{4}$ =1 B、 $\frac{x^{2}}{4}$ ﹣ $y^{2}$ =1 C、 $\frac{y^{2}}{4}$ ﹣ $x^{2}$ =1 D、 $y^{2}$ ﹣ $\frac{x^{2}}{4}$ =1

查看试题解析
9. 直三棱柱ABC﹣A₁B₁C₁中，若∠BAC=90°，AB=AC=AA₁ ，则异面直线BA₁与AC₁所成的角等于（）

A、30° B、45° C、60° D、90°

查看试题解析
10. 已知椭圆E： $\frac{x^{2}}{a^{2}}$ + $\frac{y^{2}}{b^{2}}$ =1（a＞b＞0）的右焦点为F，短轴的一个端点为M，直线l：3x﹣4y=0交椭圆E于A，B两点，若|AF|+|BF|=4，点M到直线l的距离不小于 $\frac{4}{5}$ ，则椭圆E的离心率的取值范围是（　　）

A、（0， $\frac{\sqrt{3}}{2}$ ] B、（0， $\frac{3}{4}$ ] C、[ $\frac{\sqrt{3}}{2}$ ， 1） D、[ $\frac{3}{4}$ ， 1）

查看试题解析

二、填空题

11. 已知椭圆 $\frac{x^{2}}{16}$ + $\frac{y^{2}}{9}$ =1，F₁ ， F₂是椭圆的两个焦点，则|F₁F₂|=

查看试题解析
12. 若△ABC中，AC= $\sqrt{6}$ ， A=45°，C=75°，则BC=

查看试题解析
13. 若“∀x∈[0， $\frac{π}{4}$ ]，tanx≤m”是真命题，则实数m的最小值为

查看试题解析
14. 若数列{a_n}的前n项和S_n= $\frac{2}{3}$ a_n﹣ $\frac{2}{3}$ ，则数列{a_n}的通项公式a_n=

查看试题解析
15. 若“m﹣1＜x＜m+1”是“x²﹣2x﹣3＞0”的充分不必要条件，则实数m的取值范围是

查看试题解析

三、解答题

16. 已知a，b，c分别是△ABC内角A，B，C的对边，sin²B=2sinAsinC．
（Ⅰ）若a=b，求cosB；
（Ⅱ）设B=90°，且a= $\sqrt{2}$ ，求△ABC的面积．

查看试题解析
17. 已知等差数列{a_n}的前n项的和记为S_n ．如果a₄=﹣12，a₈=﹣4．
（1）求数列{a_n}的通项公式；
（2）求S_n的最小值及其相应的n的值．

查看试题解析
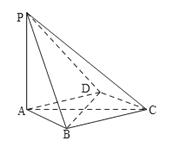
18.
如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，底面ABCD是菱形．
（1）求证：BD⊥平面PAC；
（2）若PA=AB，求PB与AC所成角的余弦值．

查看试题解析
19. 徐州、苏州两地相距500千米，一辆货车从徐州匀速行驶到苏州，规定速度不得超过100千米/小时．已知货车每小时的运输成本（以元为单位）由可变部分和固定部分组成：可变部分与速度v（千米/时）的平方成正比，比例系数为0.01；固定部分为a元（a＞0）．
（1）把全程运输成本y（元）表示为速度v（千米/时）的函数，并指出这个函数的定义域；
（2）为了使全程运输成本最小，汽车应以多大速度行驶？

查看试题解析
20. 已知椭圆C： $\frac{x^{2}}{a^{2}}$ + $\frac{y^{2}}{b^{2}}$ =1（a＞b＞0）的离心率为 $\frac{\sqrt{6}}{3}$ ，焦距为2 $\sqrt{2}$ ，过点D（1，0）且不过点E（2，1）的直线l与椭圆C交于A，B两点，直线AE与直线x=3交于点M．
（1）求椭圆C的标准方程；
（2）若AB垂直于x轴，求直线MB的斜率。

查看试题解析