初中数学湘教版八年级下学期期中复习专题7 三角形的中位线
试卷更新日期：2021-04-01 类型：复习试卷
一、单选题
-
1. 如图，要测量被池塘隔开的A，B两点的距离，小明在AB外选一点C，连接AC，BC，并分别找出它们的中点D，E，连接DE，现测得DE=45米，那么AB等于（ ）
A、90米 B、88米 C、86米 D、84米2. 如图，在四边形ABCD中，R，P分别是BC，CD上的点，E，F分别是AP，RP的中点，当点P在CD上从点C向点D移动而点R不动时，下列结论成立的是（ ）
A、线段EF的长逐渐增大 B、线段EF的长逐渐减小 C、线段EF的长不变 D、线段EF的长与点P的位置有关3. 如图，在 中， ， ， ，点 ， ， 分别是 三边中点，则 的周长为（ ）
A、 B、 C、 D、4. 如图，已知矩形ABCD中，R， P分别是DC，BC上的点，E，F分别是AP，RP的中点.当点P在BC上从点B向点C移动而点R不动时，那么下列结论成立的是（ ）.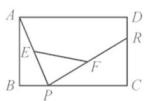
A、线段EF的长逐渐增大 B、线段EF的长逐渐减少 C、线段EF的长不变 D、线段EF的长不能确定5. 如图，△ABC的中线BD，CE交于点O，连接OA，点G，F分别为OC，OB的中点，BC=8，A0=6，则四边形DEFG的周长为（ ）.
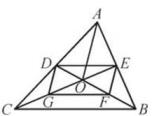A、12 B、14 C、16 D、186. 三角形的三条中位线长分别为2cm、3cm、4cm，则原三角形的周长为（ ）.A、4.5cm B、18cm C、9cm D、36cm7. 如图，△ABC中，点D、E分别在AB、AC边上，AD=BD，AE=EC，BC=6，则DE=（ ）
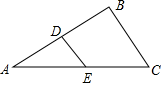A、4 B、3 C、2 D、58. 如图所示，▱ABCD的对角线AC，BD相交于点O，点E是CD的中点，若BC＝6，则OE的长为（ ）
A、2 B、2.5 C、3 D、49.如图，在一张△ABC纸片中，∠C=90°，∠B=60°，DE是中位线，现把纸片沿中位线DE剪开，计划拼出以下四个图形：①邻边不等的矩形；②等腰梯形；③有一个角为锐角的菱形；④正方形．那么以上图形一定能被拼成的个数为（ ）
A、1 B、2 C、3 D、410. 如图，已知四边形ABCD中，R、P分别是BC、CD上的点，E、F分别是AP、RP的中点，当点P在CD上从C向D移动而点R不动时，那么下列结论成立的是（ ）
A、线段EF的长逐渐增大 B、线段EF的长逐渐减小 C、线段EF的长不变 D、线段EF的长与点P的位置有关二、填空题
-
11. 如图，在△ABC中，P ， Q分别为AB ， AC的中点．若S△APQ＝1，则S四边形PBCQ＝ ．
12. 如图，在△MBN 中，已知：BM＝6，BN＝7，MN＝10，点 A C，D 分别是 MB，NB，MN 的中点，则四边形 ABCD 的周长 是 ．
13. 如图是跷跷板的示意图，立柱 与地面垂直，以 为横板 的中点， 绕点 上下转动，横板 的 端最大高度 是否会随横板长度的变化而变化呢？一位同学做了如下研究：他先设 ， ，通过计算得到此时的 ，再将横板 换成横板 ， 为横板 的中点，且 ，此时 点的最大高度为 ，由此得到 与 的大小关系是： （填“ 、“ ”或“ ”）可进一步得出， 随横板的长度的变化而（填“不变”或“改变”）．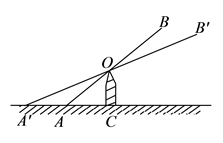
14. 如图，在图（1）中，A1、B1、C1分别是△ABC的边BC、CA、AB的中点，在图（2）中，A2、B2、C2分别是△A1B1C1的边B1C1、C1A1、A1B1的中点，…，按此规律，则第n个图形中平行四边形的个数共有个
15. 如图，已知△ABC中，AB=AC，AD平分∠BAC，E是AB的中点，若AC=6，则DE的长为
16. 如图，△ABC中，D、E分别是BC、AC的中点，BF平分∠ABC，交DE于点F，若BC＝6，则DF的长是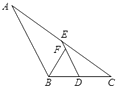
三、解答题
-
17.
如图，点D、E是Rt△ABC两直角边AB、AC上的一点，连接BE，已知点F、G、H分别是DE、BE、BC的中点．
（1）求∠FGH度数；
（2）连CD，取CD中点M，连接GM，若BD=8，CE=6，求GM的长．
18. 如图，四边形ABCD中，已知AB=CD，点E、F分别为AD、BC的中点，延长BA、CD，分别交射线FE于P、Q两点．求证：∠BPF=∠CQF．
19.如图，M是△ABC的边BC的中点，AN平分∠BAC，且BN⊥AN，垂足为N，且AB=6，BC=10，MN=1.5，求△ABC的周长．
四、综合题
