初中数学湘教版八年级下学期期中复习专题9菱形的性质与判定
试卷更新日期:2021-04-01 类型:复习试卷
一、单选题
-
1. 如图,若菱形ABCD的对角线AC,BD的长分别为6和8,则这个菱形的周长是( )
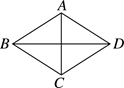 A、20 B、24 C、40 D、482. 菱形具有而一般平行四边形不具有的性质是( )A、对边相等 B、对角相等 C、对角线互相垂直 D、对角线互相平分3. 如图,在菱形ABCD中,AC、BD相交于点O,E为AB的中点,且DE⊥AB,AC=6,则菱形ABCD的面积是( )
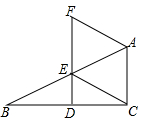
A、20 B、24 C、40 D、482. 菱形具有而一般平行四边形不具有的性质是( )A、对边相等 B、对角相等 C、对角线互相垂直 D、对角线互相平分3. 如图,在菱形ABCD中,AC、BD相交于点O,E为AB的中点,且DE⊥AB,AC=6,则菱形ABCD的面积是( )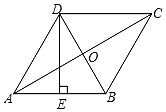 A、18 B、18
A、18 B、18 C、9
C、9  D、6
D、6  4. 如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的中点,则MP+PN的最小值是( )
4. 如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的中点,则MP+PN的最小值是( )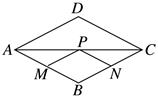 A、
A、 B、1
C、
D、2
5. 如图,已知菱形ABCD的对角线交于点O,DB=6,AD=5,则菱形ABCD的面积为( )
B、1
C、
D、2
5. 如图,已知菱形ABCD的对角线交于点O,DB=6,AD=5,则菱形ABCD的面积为( ) A、20 B、24 C、30 D、366. 下列给出的条件中,能判定一个四边形是菱形的是( )A、一组对边平行且相等,有一个角是直角 B、两组对边分别相等,并且有一条对角线平分一组内角 C、两条对角线互相平分,并且有一组邻角相等 D、一组对边平行,一组对边相等,并且对角线互相垂直7. 如图,四边形 是平行四边形,要使它变成菱形,需要添加的条件是( )
A、20 B、24 C、30 D、366. 下列给出的条件中,能判定一个四边形是菱形的是( )A、一组对边平行且相等,有一个角是直角 B、两组对边分别相等,并且有一条对角线平分一组内角 C、两条对角线互相平分,并且有一组邻角相等 D、一组对边平行,一组对边相等,并且对角线互相垂直7. 如图,四边形 是平行四边形,要使它变成菱形,需要添加的条件是( )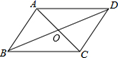 A、AC=BD B、AD=BC C、AB=BC D、AB=CD8.
A、AC=BD B、AD=BC C、AB=BC D、AB=CD8.如图,在四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点,要使四边形EFGH是菱形,则四边形ABCD只需要满足一个条件,是( )
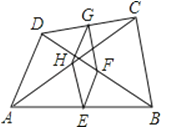 A、四边形ABCD是梯形 B、四边形ABCD是菱形 C、对角线AC=BD D、AD=BC9. 在四边形ABCD中,对角线AC、BD相交于点O,给出下列条件:①AB∥CD; ②AB=CD; ③OA=OC;④OB=OD; ⑤AC⊥BD;⑥AC平分∠BAD.则下列各组组合中,不能推出四边形ABCD为菱形的是( )A、①②④ B、③④⑤ C、①②⑤ D、①②⑥10. 一个菱形的周长为8cm,高为1cm,这个菱形两邻角度数之比为( )A、3:1 B、4:1 C、5:1 D、6:1
A、四边形ABCD是梯形 B、四边形ABCD是菱形 C、对角线AC=BD D、AD=BC9. 在四边形ABCD中,对角线AC、BD相交于点O,给出下列条件:①AB∥CD; ②AB=CD; ③OA=OC;④OB=OD; ⑤AC⊥BD;⑥AC平分∠BAD.则下列各组组合中,不能推出四边形ABCD为菱形的是( )A、①②④ B、③④⑤ C、①②⑤ D、①②⑥10. 一个菱形的周长为8cm,高为1cm,这个菱形两邻角度数之比为( )A、3:1 B、4:1 C、5:1 D、6:1二、填空题
-
11. 已知菱形两条对角线的长分别为5cm和12cm,则这个菱形的面积是cm2.12. 菱形的面积为24,一条对角线长为6,则它的周长是.13. 如图,在菱形ABCD中,∠BAD=70°,AB的垂直平分线交对角线AC于点F,E为垂足,连接DF,则∠CDF=°.
 14. 如图,ABCD是对角线互相垂直的四边形,且0B=OD,请你添加一个适当的条件: 使ABCD成为菱形.(只需添加一个即可)
14. 如图,ABCD是对角线互相垂直的四边形,且0B=OD,请你添加一个适当的条件: 使ABCD成为菱形.(只需添加一个即可) 15. 如图,剪两张等宽对边平行的纸条,随意交叉叠放在一起,转动其中的一张,重合的部分构成了一个四边形,这个四边形是 .
15. 如图,剪两张等宽对边平行的纸条,随意交叉叠放在一起,转动其中的一张,重合的部分构成了一个四边形,这个四边形是 .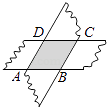
三、解答题
-
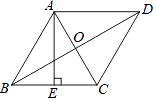
16. 如图,菱形ABCD对角线AC、BD交于点O,其中AC=6,BD=8,AE⊥BC于点E,求AE的长度.
 17. 已知:如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
17. 已知:如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.求证:四边形BCFE是菱形.

四、综合题