云南省昭通市昭阳区2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-04-01 类型:期末考试
一、填空题
-
1. 已知方程 的一个根是2,则c的值是 .2. 物线 的顶点坐标是 .3. 点 与点Q关于原点成中心对称,则点Q的坐标为 .4. 一个不透明的盒子里装有除颜色外无其他差别的白珠子6颗和黑珠子若干颗,每次随机摸出一颗珠子,放回摇匀后再摸,通过多次试验发现摸到白珠子的频率稳定在0.3左右,则盒子中黑珠子可能有 颗.5. 已知圆锥的母线长为 ,高为 ,则该圆锥的展开图(扇形)的弧长为(结果保留 ).6. 如图,在四边形 中, 、 是对角线, ,如果 ,那么 .

二、单选题
-
7. 下列方程中,一元二次方程共有( )
① ② ③ ④ ⑤
A、2个 B、3个 C、4个 D、5个8. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 9. 去年昭阳区参加中考人数约为14400人,这个数用科学记数法表示是( )A、 B、 C、 D、10.
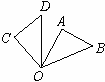
9. 去年昭阳区参加中考人数约为14400人,这个数用科学记数法表示是( )A、 B、 C、 D、10.如图,△OAB绕点O逆时针旋转80°到△OCD的位置,已知∠AOB=45°,则∠AOD等于( )
 A、35° B、40° C、45° D、55°11. 若x1 , x2是一元二次方程x2+10x+16=0的两个根,则x1+x2的值是( )A、﹣10 B、10 C、﹣16 D、1612.
A、35° B、40° C、45° D、55°11. 若x1 , x2是一元二次方程x2+10x+16=0的两个根,则x1+x2的值是( )A、﹣10 B、10 C、﹣16 D、1612.如图,两个同心圆的半径分别为3cm和5cm,弦AB与小圆相切于点C , 则AB的长为( )
 A、4cm B、5cm C、6cm D、8cm13. 边长为 的正六边形的面积等于( )A、 B、 C、 D、14. 如图,在 中, ,分别以 、 为直径作半圆,则图中阴影部分的面积是( )
A、4cm B、5cm C、6cm D、8cm13. 边长为 的正六边形的面积等于( )A、 B、 C、 D、14. 如图,在 中, ,分别以 、 为直径作半圆,则图中阴影部分的面积是( ) A、 B、 C、 D、
A、 B、 C、 D、三、解答题
-
15. 解方程:(1)、(2)、16. 先化简,再求值: ,其中 .17. 如图,在 中,已知 , 平分 ,点M,N分别在 , 边上, .

求证: .
18. 如图, 三个顶点的坐标分别为 . (1)、请画出 关于 轴对称的 ,并写出点 的坐标;(2)、请画出 绕点 逆时针旋转 后的 ;19. 某地区2018年投人教育经费2.5亿元,2020年投入教育经费3.025亿元.求2018年至2020年该地区投入教育经费的年平均增长率?20. 现有一个六面分别标有数字1,2,3,4,5,6且质地均匀的正方形骰子,另有三张正面分别标有数字1,2,3的卡片(卡片除数字外,其他都相同),先由小明投骰子一次,记下骰子向上一面出现的数字,然后由小王从三张背面朝上放置在桌面上的卡片中随机抽取一张,记下卡片上的数字.(1)、请用列表或画树形图(树状图)的方法,求出骰子向上一面出现的数字与卡片上的数字之积为6的概率(2)、小明和小王做游戏,约定游戏规则如下:若骰子向上一面出现的数字与卡片上的数字之积大于7,则小明赢;若骰子向上一面出现的数字与卡片上的数字之积小于7,则小王赢,问小明和小王谁赢的可能性更大?请说明理由.
(1)、请画出 关于 轴对称的 ,并写出点 的坐标;(2)、请画出 绕点 逆时针旋转 后的 ;19. 某地区2018年投人教育经费2.5亿元,2020年投入教育经费3.025亿元.求2018年至2020年该地区投入教育经费的年平均增长率?20. 现有一个六面分别标有数字1,2,3,4,5,6且质地均匀的正方形骰子,另有三张正面分别标有数字1,2,3的卡片(卡片除数字外,其他都相同),先由小明投骰子一次,记下骰子向上一面出现的数字,然后由小王从三张背面朝上放置在桌面上的卡片中随机抽取一张,记下卡片上的数字.(1)、请用列表或画树形图(树状图)的方法,求出骰子向上一面出现的数字与卡片上的数字之积为6的概率(2)、小明和小王做游戏,约定游戏规则如下:若骰子向上一面出现的数字与卡片上的数字之积大于7,则小明赢;若骰子向上一面出现的数字与卡片上的数字之积小于7,则小王赢,问小明和小王谁赢的可能性更大?请说明理由.

