云南省文山壮族苗族自治州文山市2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-04-01 类型:期末考试
一、填空题
-
1. 菱形的周长为20cm,一条对角线长为8cm,则菱形的面积为 cm2.
2. 已知某几何体的三视图如图所示,其中俯视图为正六边形,则该几何体的表面积为 . 3. 在国家政策的宏观调控下,某市的商品房成交均价由去年10月份的7000元/m2下降到12月份的5670元/m2 , 则11、12两月平均每月降价的百分率是%。
3. 在国家政策的宏观调控下,某市的商品房成交均价由去年10月份的7000元/m2下降到12月份的5670元/m2 , 则11、12两月平均每月降价的百分率是%。
4. 如图,在边长为4的正方形ABCD中,E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,则△BEQ周长的最小值为 . 5. 如图,反比例函数y= (x>0)的图象经过矩形OABC的边AB的中点D,若矩形OABC的面积为8,则k= .
5. 如图,反比例函数y= (x>0)的图象经过矩形OABC的边AB的中点D,若矩形OABC的面积为8,则k= . 6. 如图,等边△ABC的边长为3,点P为BC上一点,且BP=1,点D为AC上一点,若∠APD=60°,则CD的长为.
6. 如图,等边△ABC的边长为3,点P为BC上一点,且BP=1,点D为AC上一点,若∠APD=60°,则CD的长为.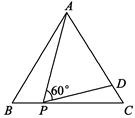
二、单选题
-
7. 在一个不透明的口袋中装有4个红球和若干个白球,他们除颜色外其他完全相同.通过多次摸球实验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有( )A、16个 B、15个 C、13个 D、12个8. 关于x的一元二次方程x2-mx+2m-1=0的两个实数根分别是x1、x2 , 且x12+x22=7,则(x1-x2)2的值是( )A、1 B、12 C、13 D、259. 一次函数y=ax+b与反比例函数y= ,其中ab<0,a、b为常数,它们在同一坐标系中的图象可以是( )A、
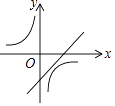 B、
B、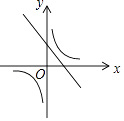 C、
C、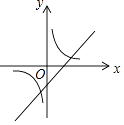 D、
D、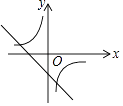 10. 菱形OABC在平面直角坐标系中的位置如图所示.∠AOC=45°,OC= , 则点B的坐标为( )
10. 菱形OABC在平面直角坐标系中的位置如图所示.∠AOC=45°,OC= , 则点B的坐标为( )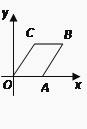 A、( , 1) B、(1,) C、(+1,1) D、(1,+1)11. 如图,正方形ABCD的边长为4,点E在对角线BD上,且 ,EF⊥AB,垂足为F,则EF的长为( )
A、( , 1) B、(1,) C、(+1,1) D、(1,+1)11. 如图,正方形ABCD的边长为4,点E在对角线BD上,且 ,EF⊥AB,垂足为F,则EF的长为( )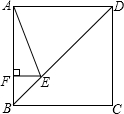 A、1 B、 C、 D、12. 如图,正比例函数 的图像与反比例函数 的图象相交于A、B两点,其中点A的横坐标为2,当 时,x的取值范围是( )
A、1 B、 C、 D、12. 如图,正比例函数 的图像与反比例函数 的图象相交于A、B两点,其中点A的横坐标为2,当 时,x的取值范围是( ) A、x<-2或x>2 B、x<-2或0<x<2 C、-2<x<0或0<x<2 D、-2<x<0或x>213. 如图,菱形ABCD的周长为8cm,高AE长为 cm,则对角线AC长和BD长之比为( )
A、x<-2或x>2 B、x<-2或0<x<2 C、-2<x<0或0<x<2 D、-2<x<0或x>213. 如图,菱形ABCD的周长为8cm,高AE长为 cm,则对角线AC长和BD长之比为( ) A、1:2 B、1:3 C、1:
A、1:2 B、1:3 C、1: D、1:
D、1:  14. 如图,在△ABC中,中线BE、CD相交于点O , 连接DE , 下列结论:① ;② ;③ ;④ ;其中正确的个数有( )
14. 如图,在△ABC中,中线BE、CD相交于点O , 连接DE , 下列结论:① ;② ;③ ;④ ;其中正确的个数有( )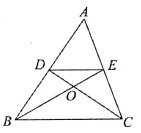 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个三、解答题
-
15. 已知关于x 的一元二次方程:.x2﹣(t﹣1)x+t﹣2=0(1)、求证:对于任意实数t,方程都有实数根;(2)、当
 为何值时,方程的两个根互为相反数?请说明理由. 16. 已知m是方程 的一个根,试求 的值.17. 某超市计划在“十周年”庆典当天开展购物抽奖活动,凡当天在该超市购物的顾客,均有一次抽奖的机会,抽奖规则如下:将如图所示的圆形转盘平均分成四个扇形,分别标上1,2,3,4四个数字,抽奖者连续转动转盘两次,当每次转盘停止后指针所指扇形内的数为每次所得的数(若指针指在分界线时重转);当两次所得数字之和为8时,返现金20元;当两次所得数字之和为7时,返现金15元;当两次所得数字之和为6时返现金10元.
为何值时,方程的两个根互为相反数?请说明理由. 16. 已知m是方程 的一个根,试求 的值.17. 某超市计划在“十周年”庆典当天开展购物抽奖活动,凡当天在该超市购物的顾客,均有一次抽奖的机会,抽奖规则如下:将如图所示的圆形转盘平均分成四个扇形,分别标上1,2,3,4四个数字,抽奖者连续转动转盘两次,当每次转盘停止后指针所指扇形内的数为每次所得的数(若指针指在分界线时重转);当两次所得数字之和为8时,返现金20元;当两次所得数字之和为7时,返现金15元;当两次所得数字之和为6时返现金10元.
(1)、试用树状图或列表的方法表示出一次抽奖所有可能出现的结果(2)、某顾客参加一次抽奖,能获得返还现金的概率是多少?18. 如图,在平面直角坐标系 中,一次函数 的图象与 轴交于点 ,与反比例函数 在第一象限内的图象交于点 ,且点 的横坐标为 .过点 作 轴交反比例函数 的图象于点 ,连接 . (1)、求反比例函数的表达式.(2)、求 的面积.19. 如图,在 ABC中,点F是BC的中点,点E是线段AB的延长线上的一动点,连接EF,过点C作AB的平行线CD,与线段EF的延长线交于点D,连接CE,BD.
(1)、求反比例函数的表达式.(2)、求 的面积.19. 如图,在 ABC中,点F是BC的中点,点E是线段AB的延长线上的一动点,连接EF,过点C作AB的平行线CD,与线段EF的延长线交于点D,连接CE,BD. (1)、求证:四边形DBEC是平行四边形.(2)、若 , ,则在点E的运动过程中:
(1)、求证:四边形DBEC是平行四边形.(2)、若 , ,则在点E的运动过程中:①当BE= ▲ 时,四边形BECD是矩形,试说明理由;
②当BE= ▲ 时,四边形BECD是菱形.
20. 如图,有长为24米的篱笆,一面利用墙(墙的最大可用长度为11米)围成中间隔有一道篱笆的长方形花圃.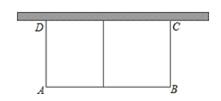 (1)、如果要围成面积为45平方米的花圃,那么AD的长为多少米?(2)、能否围成面积为60平方米的花圃?若能,请求出AD的长;若不能,请说明理由.21. 如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且 .
(1)、如果要围成面积为45平方米的花圃,那么AD的长为多少米?(2)、能否围成面积为60平方米的花圃?若能,请求出AD的长;若不能,请说明理由.21. 如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且 .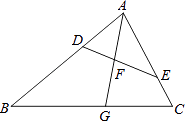 (1)、求证:△ADF∽△ACG;(2)、若 ,求 的值.22. 某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y (℃)与时间x(h)之间的函数关系,其中线段AB、BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.
(1)、求证:△ADF∽△ACG;(2)、若 ,求 的值.22. 某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y (℃)与时间x(h)之间的函数关系,其中线段AB、BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.请根据图中信息解答下列问题:
 (1)、求这天的温度y与时间x(0≤x≤24)的函数关系式;
(1)、求这天的温度y与时间x(0≤x≤24)的函数关系式;
(2)、求恒温系统设定的恒定温度;(3)、若大棚内的温度低于10℃时,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多少小时,才能使蔬菜避免受到伤害?23. 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB , D为AB边上一点,过点D作DE⊥BC , 交直线MN于E , 垂足为F , 连接CD、BE .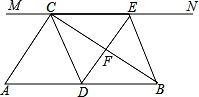 (1)、求证:CE=AD;(2)、当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;(3)、若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
(1)、求证:CE=AD;(2)、当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;(3)、若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.