云南省昆明市官渡区2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-04-01 类型:期末考试
一、填空题
-
1. 若方程 是关于 的一元二次方程,则 的取值范围是 .2. 若点 在二次函数 的图象上,则 .3. 为了解今年从西伯利亚飞到昆明过冬的红嘴鸥的数量,某研究团队给200只红嘴鸥做上标记,经过一段时间,当带有标记的红嘴鸥和其它不带标记的红嘴鸥完全混合后,再次观察发现416只红嘴鸥中有2只带有标记,那么由此可以估计今年飞到昆明过冬的红嘴鸥大约有只.4. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=3cm,扇形的圆心角θ=120°,则该圆锥的母线长 为cm.
 5. 如图,在平面直角坐标系中,正六边形 的边长是2,则它的外接圆圆心 的坐标是 .
5. 如图,在平面直角坐标系中,正六边形 的边长是2,则它的外接圆圆心 的坐标是 .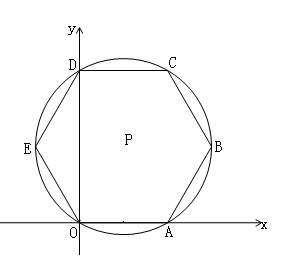 6. 如图, , 分别与 相切于点 ,点 , , 是 上异于 , 的点,则 的度数为 .
6. 如图, , 分别与 相切于点 ,点 , , 是 上异于 , 的点,则 的度数为 .
二、单选题
-
7. 下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )A、
 赵爽弦图
B、
赵爽弦图
B、 笛卡尔心形线
C、
笛卡尔心形线
C、 科克曲线
D、
科克曲线
D、 斐波那契螺旋线
8. 关于 的方程 的一个根是 ,则它的另一个根 是( )A、0 B、1 C、-1 D、29. 下列说法错误的是( )A、“三角形任意两边之和小于第三边”是不可能事件 B、“篮球队员在罚球线上投篮一次,投中”为随机事件 C、某种彩票的中奖率是 ,说明每买100张彩票,一定有1张中奖 D、“在同一年出生的367人中,至少有两人的生日相同”是必然事件10. 下列一元二次方程没有实数根的是( )A、 B、 C、 D、11. 抛物线 经过平移得到抛物线 ,平移的方法是( )A、向左平移1个单位,再向下平移2个单位 B、向右平移1个单位,再向下平移2个单位 C、向左平移1个单位,再向上平移2个单位 D、向右平移1个单位,再向上平移2个单位12. 《生物多祥性公约》第十五次缔约方大会(COP15)将于2021年5月17日至30日在云南省昆明市举办、昆明某景观园林公司为迎接大会召开,计划在一个长为 ,塞为 的矩形场地 (如图所示)上修建三条同样宽的道路,使其中两条与 平行、另一条与 平行,其余部分种草坪,若使每一块草坪的面积为 ,求道路的宽度、若设道路的宽度为 ,则 满足的方程为( )
斐波那契螺旋线
8. 关于 的方程 的一个根是 ,则它的另一个根 是( )A、0 B、1 C、-1 D、29. 下列说法错误的是( )A、“三角形任意两边之和小于第三边”是不可能事件 B、“篮球队员在罚球线上投篮一次,投中”为随机事件 C、某种彩票的中奖率是 ,说明每买100张彩票,一定有1张中奖 D、“在同一年出生的367人中,至少有两人的生日相同”是必然事件10. 下列一元二次方程没有实数根的是( )A、 B、 C、 D、11. 抛物线 经过平移得到抛物线 ,平移的方法是( )A、向左平移1个单位,再向下平移2个单位 B、向右平移1个单位,再向下平移2个单位 C、向左平移1个单位,再向上平移2个单位 D、向右平移1个单位,再向上平移2个单位12. 《生物多祥性公约》第十五次缔约方大会(COP15)将于2021年5月17日至30日在云南省昆明市举办、昆明某景观园林公司为迎接大会召开,计划在一个长为 ,塞为 的矩形场地 (如图所示)上修建三条同样宽的道路,使其中两条与 平行、另一条与 平行,其余部分种草坪,若使每一块草坪的面积为 ,求道路的宽度、若设道路的宽度为 ,则 满足的方程为( ) A、 B、 C、 D、13. 已知二次函数 的图象如图所示,对称轴是直线 ,下列结论:① ;② ;③ ;④ ,其中正确的个数是( )
A、 B、 C、 D、13. 已知二次函数 的图象如图所示,对称轴是直线 ,下列结论:① ;② ;③ ;④ ,其中正确的个数是( )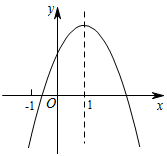 A、1 B、2 C、3 D、414. 如图,抛物线 与 轴交于 , 两点, 是以点 为圆心, 为半径的圆上的动点, 是线段 的中点,连结 、则线段 的最大值是( )
A、1 B、2 C、3 D、414. 如图,抛物线 与 轴交于 , 两点, 是以点 为圆心, 为半径的圆上的动点, 是线段 的中点,连结 、则线段 的最大值是( ) A、 B、3 C、 D、
A、 B、3 C、 D、三、解答题
-
15. 用适当的方法解方程(1)、(2)、16. 如图, 三个顶点坐标分别为 , , .
 (1)、请画出 关于原点 中心对称的图形 ,并直接写出点 的坐标:(2)、请画出 绕原点 逆时针旋转90°的图形 ,并直接写出点 的坐标:(3)、求在(2)的旋转过程中,点 旋转到 所经过的路径长(结果保留 )17. 2020年3月,新冠肺炎疫情在中国已经得到有效控制,但在全球却开始持续蔓延,这是对人类的考验,将对全球造成巨大影响.新冠肺炎具有人传人的特性,若一人携带病毒,未进行有效隔离,经过两轮传染后共有169人患新冠肺炎(假设每轮传染的人数相同).求:(1)、每轮传染中平均每个人传染了几个人?(2)、如果这些病毒携带者,未进行有效隔离,按照这样的传染速度,第三轮传染后,共有多少人患病?18. 如图,在 中, , ,点 在 上,将 绕点 顺时针方向旋转90°后,得到 .
(1)、请画出 关于原点 中心对称的图形 ,并直接写出点 的坐标:(2)、请画出 绕原点 逆时针旋转90°的图形 ,并直接写出点 的坐标:(3)、求在(2)的旋转过程中,点 旋转到 所经过的路径长(结果保留 )17. 2020年3月,新冠肺炎疫情在中国已经得到有效控制,但在全球却开始持续蔓延,这是对人类的考验,将对全球造成巨大影响.新冠肺炎具有人传人的特性,若一人携带病毒,未进行有效隔离,经过两轮传染后共有169人患新冠肺炎(假设每轮传染的人数相同).求:(1)、每轮传染中平均每个人传染了几个人?(2)、如果这些病毒携带者,未进行有效隔离,按照这样的传染速度,第三轮传染后,共有多少人患病?18. 如图,在 中, , ,点 在 上,将 绕点 顺时针方向旋转90°后,得到 . (1)、求 的度数;(2)、若 , ,求 的长.19. 如图, 内接于 , 是 上的一点,连接 , , .
(1)、求 的度数;(2)、若 , ,求 的长.19. 如图, 内接于 , 是 上的一点,连接 , , . (1)、求证:(2)、若 , ,求 的半径.20. 为了让广大学子通过身边的故事,深刻感受伟大祖国“十三五”时期的发展建设成就,畅想未来美好蓝图,由教育部组织的“我和我的学校”网络微视频接力活动于近期启动,活动分为两个阶段,第一阶段以“记住这些年”为主题,第二阶段以“追梦2035”为主题.昆明某校学生准备从4个不同的素材 , , , 中选取一个参加第一阶段的主题活动,从3个不同的素材 , , 中选取一个参加第二阶段的主题活动.现将这两个阶段的7个素材分别写在形状大小质地都相同的卡片上.(1)、如果把所有卡片混在一起,张月同学一次抽中第二阶段活动素材的概率是 .(2)、李华同学对第一阶段的素材 , 和第二阶段的素材 , 准备得较好,如果第一次抽签确定第一阶段活动内容,第二次抽签确定第二阶段活动内容.请用列表或画树状图的方法,求他抽到的两个素材都准备得较好的概率.21. 昆明斗南花卉市场是全国鲜花市场的心脏,也是亚洲最大的鲜花交易市场之一.斗南某兰花专卖店专门销售某种品牌的兰花,已知这种兰花的成本价为60元/盆.市场管理部门规定:每盆兰花的销售价格不低于成本价,又不高于成本价的2倍.经过市场调查发现,该店某天的销售数量 (盆)与销售单价 (元/盆)之间的函数关系如图所示:
(1)、求证:(2)、若 , ,求 的半径.20. 为了让广大学子通过身边的故事,深刻感受伟大祖国“十三五”时期的发展建设成就,畅想未来美好蓝图,由教育部组织的“我和我的学校”网络微视频接力活动于近期启动,活动分为两个阶段,第一阶段以“记住这些年”为主题,第二阶段以“追梦2035”为主题.昆明某校学生准备从4个不同的素材 , , , 中选取一个参加第一阶段的主题活动,从3个不同的素材 , , 中选取一个参加第二阶段的主题活动.现将这两个阶段的7个素材分别写在形状大小质地都相同的卡片上.(1)、如果把所有卡片混在一起,张月同学一次抽中第二阶段活动素材的概率是 .(2)、李华同学对第一阶段的素材 , 和第二阶段的素材 , 准备得较好,如果第一次抽签确定第一阶段活动内容,第二次抽签确定第二阶段活动内容.请用列表或画树状图的方法,求他抽到的两个素材都准备得较好的概率.21. 昆明斗南花卉市场是全国鲜花市场的心脏,也是亚洲最大的鲜花交易市场之一.斗南某兰花专卖店专门销售某种品牌的兰花,已知这种兰花的成本价为60元/盆.市场管理部门规定:每盆兰花的销售价格不低于成本价,又不高于成本价的2倍.经过市场调查发现,该店某天的销售数量 (盆)与销售单价 (元/盆)之间的函数关系如图所示: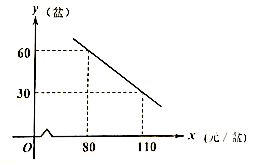 (1)、求 与 之间的函数关系式,并写出自变量 的取值范围:(2)、在销售过程中,该店每天还要支付其他费用200元,求这一天销售兰花获得的利润 (元)的最大值.22. 如图, 是 的直径,点 和点 是 上的两点,连接 , , ,过点 作射线交 的延长线于点 ,使 .
(1)、求 与 之间的函数关系式,并写出自变量 的取值范围:(2)、在销售过程中,该店每天还要支付其他费用200元,求这一天销售兰花获得的利润 (元)的最大值.22. 如图, 是 的直径,点 和点 是 上的两点,连接 , , ,过点 作射线交 的延长线于点 ,使 . (1)、求证: 是 的切线:(2)、若 ,求阴影部分的面积.23. 如图①,抛物线 与 轴交于 , 两点,与 轴交于点 .
(1)、求证: 是 的切线:(2)、若 ,求阴影部分的面积.23. 如图①,抛物线 与 轴交于 , 两点,与 轴交于点 .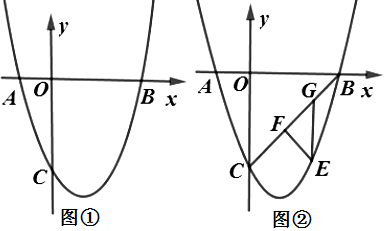
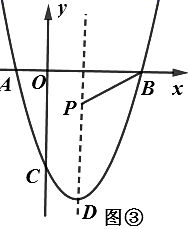 (1)、求抛物线 的解析式;(2)、如图②,连接 ,点 是第三象限内抛物线上的动点,过点 作 于点 , 轴交 于点 ,求 面积的最大值及此时点 的坐标;(3)、如图③,若抛物线的顶点坐标为点 ,点 是抛物线对称轴上的动点,在坐标平面内是否存在点 ,使得以 , , , 为顶点的四边形是菱形?若存在,求出点 的坐标;若不存在,请说明理由.
(1)、求抛物线 的解析式;(2)、如图②,连接 ,点 是第三象限内抛物线上的动点,过点 作 于点 , 轴交 于点 ,求 面积的最大值及此时点 的坐标;(3)、如图③,若抛物线的顶点坐标为点 ,点 是抛物线对称轴上的动点,在坐标平面内是否存在点 ,使得以 , , , 为顶点的四边形是菱形?若存在,求出点 的坐标;若不存在,请说明理由.