云南省红河哈尼族彝族自治州元阳县2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-04-01 类型:期末考试
一、填空题
-
1. 如果将抛物线y=x2向上平移3个单位,那么所得新抛物线的表达式是 .2. 在平面直角坐标系中,点 关于原点对称的点的坐标为.3. 方程 的根是.4. 如图,正方形ABCD旋转后能与正方形CDEF重合,那么点A,B,C,D中,可以作为旋转中心的有个.
 5. 某种油菜籽在相同条件下发芽试验的结果如下:
5. 某种油菜籽在相同条件下发芽试验的结果如下:每批粒数
50
100
300
400
600
1000
发芽的频数
45
96
283
380
571
948
这种油菜籽发芽的概率的估计值是.(结果精确到0.01)
6. 在半径为5的 中,若弦 为 ,则弦 所对的圆周角的度数为.二、单选题
-
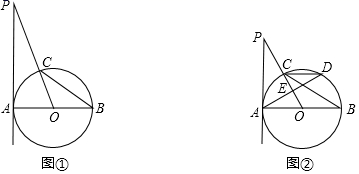
7. 已知⊙O的半径OA长为1,OB= ,则可以得到的正确图形可能是( )A、
 B、
B、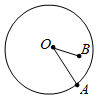 C、
C、 D、
D、 8. 下列事件为必然事件的是( )A、射击一次,中靶 B、画一个三角形,其内角和是 C、掷一枚质地均匀的硬币,正面朝上 D、12人中至少有2人的生日在同一个月9. 下列四个图案中既是轴对称图形,又是中心对称图形的是( )A、
8. 下列事件为必然事件的是( )A、射击一次,中靶 B、画一个三角形,其内角和是 C、掷一枚质地均匀的硬币,正面朝上 D、12人中至少有2人的生日在同一个月9. 下列四个图案中既是轴对称图形,又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 10. 如图,已知 是 的直径, 是弦,若 ,则 等于( )
10. 如图,已知 是 的直径, 是弦,若 ,则 等于( ) A、27° B、34° C、36° D、46°11. 关于x的一元二次方程x2+ax﹣1=0的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根12. 如图,四边形 是 的内接四边形, 的半径为12, ,则 的长为( )
A、27° B、34° C、36° D、46°11. 关于x的一元二次方程x2+ax﹣1=0的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根12. 如图,四边形 是 的内接四边形, 的半径为12, ,则 的长为( ) A、 B、 C、 D、13. 关于二次函数 ,下列说法正确的是( )A、图象的对称轴为直线 B、图象与 轴的交点坐标为 C、图象与 轴的交点坐标为 和 D、 的最小值为-914. 如图, , 分别为 的内接正三角形和内接正四边形的一边,若 恰好是同圆的一个内接正 边形的一边,则 的值为( )
A、 B、 C、 D、13. 关于二次函数 ,下列说法正确的是( )A、图象的对称轴为直线 B、图象与 轴的交点坐标为 C、图象与 轴的交点坐标为 和 D、 的最小值为-914. 如图, , 分别为 的内接正三角形和内接正四边形的一边,若 恰好是同圆的一个内接正 边形的一边,则 的值为( ) A、8 B、10 C、12 D、14
A、8 B、10 C、12 D、14三、解答题
-
15. 解方程: .16. 已知排水管的截面为如图所示的 ,半径为 ,圆心 到水面的距离是 ,求水面宽 .
 17. 如图,在平面直角坐标系中,已知 的三个顶点的坐标分别为 , , .
17. 如图,在平面直角坐标系中,已知 的三个顶点的坐标分别为 , , .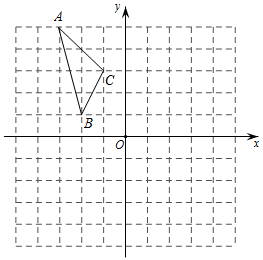 (1)、 的面积是.(2)、画出 绕着点 按顺时针方向旋转90°得到的 .18. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径 ,扇形的圆心角 ,求该圆锥的母线长 .
(1)、 的面积是.(2)、画出 绕着点 按顺时针方向旋转90°得到的 .18. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径 ,扇形的圆心角 ,求该圆锥的母线长 . 19. 小亮正在参加学校举办的趣味比赛活动,最后,他须答对两道最难的单选题才能顺利通过最后一关,其中第一题有 , , , 共4个选项,第二题有 , , 共3个选项,但是这两题小亮都不会,不过小亮有一次使用“特权”的机会(使用“特权”可去掉其中一题的一个不符合题意选项).(1)、如果小亮第一题不使用“特权”,随机选择一个选项,那么小亮答对第一题的概率是 .(2)、小亮怎样使用“特权”,才能使通过最后一关的概率大?请用画树状图或列表的方法来说明.20. 某服装店经营汉服,进价为每套145元,根据市场调查,销售单价是195元时平均每天销售量是40套,而销售价每降低10元,平均每天就可以多售出10套.假定每套汉服降价 元,服装店每天销售汉服的利润是 元.(1)、求 与 之间的函数关系式.(2)、为了薄利多销,当每套汉服售价是多少元时,服装店每天销售汉服的利润为1400元?21. 如图,△ABC中,点E在BC边上.AE=AB,将线段AC绕点A旋转到AF的位置.使得∠CAF=∠BAE.连接EF,EF与AC交于点G.
19. 小亮正在参加学校举办的趣味比赛活动,最后,他须答对两道最难的单选题才能顺利通过最后一关,其中第一题有 , , , 共4个选项,第二题有 , , 共3个选项,但是这两题小亮都不会,不过小亮有一次使用“特权”的机会(使用“特权”可去掉其中一题的一个不符合题意选项).(1)、如果小亮第一题不使用“特权”,随机选择一个选项,那么小亮答对第一题的概率是 .(2)、小亮怎样使用“特权”,才能使通过最后一关的概率大?请用画树状图或列表的方法来说明.20. 某服装店经营汉服,进价为每套145元,根据市场调查,销售单价是195元时平均每天销售量是40套,而销售价每降低10元,平均每天就可以多售出10套.假定每套汉服降价 元,服装店每天销售汉服的利润是 元.(1)、求 与 之间的函数关系式.(2)、为了薄利多销,当每套汉服售价是多少元时,服装店每天销售汉服的利润为1400元?21. 如图,△ABC中,点E在BC边上.AE=AB,将线段AC绕点A旋转到AF的位置.使得∠CAF=∠BAE.连接EF,EF与AC交于点G.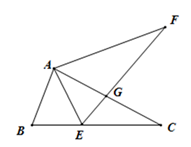 (1)、求证:EF =BC;(2)、若∠ABC=65°,∠ACB=28°,求∠FGC的度数.
(1)、求证:EF =BC;(2)、若∠ABC=65°,∠ACB=28°,求∠FGC的度数.