山东省威海市文登区2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-04-01 类型:期末考试
一、单选题
-
1. 函数 的自变 的取值范围是( )A、 B、 C、 D、 且2. 矩形的正投影不可能是( )A、线段 B、矩形 C、正方形 D、梯形3. 已知 ,那么锐角 的取值范围是( )A、 B、 C、 D、4. 将一枚飞镖投掷到如图所示的正六边形镖盘上,飞镖落在白色区域的概率为( )
 A、 B、 C、 D、5. 如图,在平地上种植树木时,要求株距(相邻两棵树之间的水平距离)为 .若在坡比为 的山坡树,也要求株距为 ,那么相邻两棵树间的坡面距离( )
A、 B、 C、 D、5. 如图,在平地上种植树木时,要求株距(相邻两棵树之间的水平距离)为 .若在坡比为 的山坡树,也要求株距为 ,那么相邻两棵树间的坡面距离( ) A、 B、 C、 D、6. 已知一个二次函数的图象经过点(2,2),顶点为( , ),将该函数图象向右平移,当他再次经过点(2,2)时,所得抛物线表达式为( )A、 B、 C、 D、7. 如图, 是 的内接三角形, 为 的直径.若 , ,则 的长度为( )
A、 B、 C、 D、6. 已知一个二次函数的图象经过点(2,2),顶点为( , ),将该函数图象向右平移,当他再次经过点(2,2)时,所得抛物线表达式为( )A、 B、 C、 D、7. 如图, 是 的内接三角形, 为 的直径.若 , ,则 的长度为( )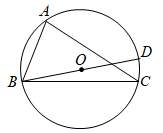 A、4 B、5 C、5.5 D、68. 某商场经营一种小商品,已知进购时单价是20元.调查发现:当销售单价是30元时,月销售量为240件,而销售单价每上涨1元,月销售量就减少10件,但每件商品的售价不能高于40元.当月销售利润最大时,销售单价为( )A、35元 B、36元 C、37元 D、36或37元9. 以坐标原点 为圆心,1为半径作圆,直线 与 相交,则 的取值范围是( )A、 B、 C、 D、10. 为预防新冠病毒,某学校每周末用药熏消毒法对教室进行消毒,已知药物释放过程中,教室内每立方米空气中含药量 与时间 成正比例;药物释放完毕后, 与 成反比例,如图所示.根据图象信息,下列选项错误的是( )
A、4 B、5 C、5.5 D、68. 某商场经营一种小商品,已知进购时单价是20元.调查发现:当销售单价是30元时,月销售量为240件,而销售单价每上涨1元,月销售量就减少10件,但每件商品的售价不能高于40元.当月销售利润最大时,销售单价为( )A、35元 B、36元 C、37元 D、36或37元9. 以坐标原点 为圆心,1为半径作圆,直线 与 相交,则 的取值范围是( )A、 B、 C、 D、10. 为预防新冠病毒,某学校每周末用药熏消毒法对教室进行消毒,已知药物释放过程中,教室内每立方米空气中含药量 与时间 成正比例;药物释放完毕后, 与 成反比例,如图所示.根据图象信息,下列选项错误的是( ) A、药物释放过程需要 小时 B、药物释放过程中, 与 的函数表达式是 C、空气中含药量大于等于 的时间为 D、若当空气中含药量降低到 以下时对身体无害,那么从消毒开始,至少需要经过4.5小时学生才能进入教室11. 如图,一副三角板 , 如图摆放,使点 与 的中点重合, 经过点 , 交 与点 .将三角板 绕点 顺时针旋转至 处, , 分别与 , 交于点 , ,则 ( )
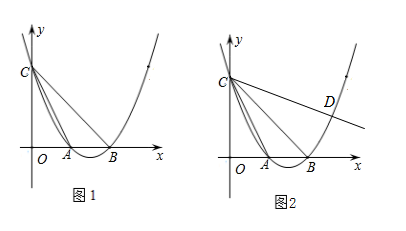
A、药物释放过程需要 小时 B、药物释放过程中, 与 的函数表达式是 C、空气中含药量大于等于 的时间为 D、若当空气中含药量降低到 以下时对身体无害,那么从消毒开始,至少需要经过4.5小时学生才能进入教室11. 如图,一副三角板 , 如图摆放,使点 与 的中点重合, 经过点 , 交 与点 .将三角板 绕点 顺时针旋转至 处, , 分别与 , 交于点 , ,则 ( ) A、 B、 C、 D、12. 如图,抛物线 交 轴于点 , ,交 轴于点 ,抛物线的顶点为 ,下列四个结论:①无论 取何值, 恒成立;②当 时, 是等腰直角三角形;③若 ,则 ;④ , 是抛物线上的两点,若 ,且 ,则 .正确的有( )
A、 B、 C、 D、12. 如图,抛物线 交 轴于点 , ,交 轴于点 ,抛物线的顶点为 ,下列四个结论:①无论 取何值, 恒成立;②当 时, 是等腰直角三角形;③若 ,则 ;④ , 是抛物线上的两点,若 ,且 ,则 .正确的有( ) A、①②③④ B、①②④ C、①② D、②③④
A、①②③④ B、①②④ C、①② D、②③④二、填空题
-
13. 计算: .14. 疫情防控期间,各学校严格落实测体温进校园的防控要求,某学校开设了 , , 三个测温通道.某天早晨,小明和小红两位同学随机通过测温通道进入校园,则小明和小红从同一通道进入校园的概率为 .15. 如图,是由一个大圆和四个相同的小圆组成的图案,若大圆的半径为2,则阴影部分的面积为 .
 16. 如图,点 在反比例函数 图象上,且 (1, ), 是第三象限内反比例函数 的图象上一个动点.过点 作 轴于点 ,过点 作 轴于点 ,连接 .若四边形 的面积为6,则点 的坐标为 .
16. 如图,点 在反比例函数 图象上,且 (1, ), 是第三象限内反比例函数 的图象上一个动点.过点 作 轴于点 ,过点 作 轴于点 ,连接 .若四边形 的面积为6,则点 的坐标为 . 17. 如图1, , 是两根垂直于地面的立柱,且长度相等.在两根立柱之间悬挂着一根绳子,如图2建立坐标系,绳子形如抛物线 的图象.因实际需要,在 与 间用一根高为 的立柱 将绳子撑起,若立柱 到 的水平距离为 , 左侧抛物线的最低点 与 的水平距离为 ,则点 到地面的距离为 .
17. 如图1, , 是两根垂直于地面的立柱,且长度相等.在两根立柱之间悬挂着一根绳子,如图2建立坐标系,绳子形如抛物线 的图象.因实际需要,在 与 间用一根高为 的立柱 将绳子撑起,若立柱 到 的水平距离为 , 左侧抛物线的最低点 与 的水平距离为 ,则点 到地面的距离为 . 18. 如图,正方形 ,对角线 , 交于点 ,以 , 为一组邻边做正方形 ; , 交于点 ,以 , 为一组邻边做正方形 ; , 交于点 ,以 , 为一组邻边做正方形 …….若 ,则 的值为 .
18. 如图,正方形 ,对角线 , 交于点 ,以 , 为一组邻边做正方形 ; , 交于点 ,以 , 为一组邻边做正方形 ; , 交于点 ,以 , 为一组邻边做正方形 …….若 ,则 的值为 .
三、解答题
-
19.(1)、先化简,再求值: ,其中 .(2)、解不等式组 .20. 如图,一个零件形如一个圆柱体削去底面圆的四分之一部分的柱体,底面圆的半径为 .
 (1)、请画出该零件的三视图;(2)、若用该零件的俯视图围成一个圆锥,求这个圆锥的高.21. 如图,有四张背面完全相同的卡片 , , , ,其中正面分别写着四个不同的函数表达式,将四张卡片洗匀正面朝下随机放在桌面上.
(1)、请画出该零件的三视图;(2)、若用该零件的俯视图围成一个圆锥,求这个圆锥的高.21. 如图,有四张背面完全相同的卡片 , , , ,其中正面分别写着四个不同的函数表达式,将四张卡片洗匀正面朝下随机放在桌面上. (1)、从四张卡片中随机摸出一张,摸出的卡片上的函数 随 的增大而减小的概率是;(2)、小亮和小强用这四张卡片做游戏,规则如下:两人同时从四张卡片中各随机抽出一张,若抽出的两张卡片上的函数增减性相同,则小亮胜;若抽出的两张卡片上的函数增减性不同,则小强胜.这个游戏公平吗?请说明理由.22. 已知反比例函数 的图象经过点 (3,4), ( , ), ( , ) , 在第三象限,顺次连接 , , .
(1)、从四张卡片中随机摸出一张,摸出的卡片上的函数 随 的增大而减小的概率是;(2)、小亮和小强用这四张卡片做游戏,规则如下:两人同时从四张卡片中各随机抽出一张,若抽出的两张卡片上的函数增减性相同,则小亮胜;若抽出的两张卡片上的函数增减性不同,则小强胜.这个游戏公平吗?请说明理由.22. 已知反比例函数 的图象经过点 (3,4), ( , ), ( , ) , 在第三象限,顺次连接 , , . (1)、求 , 的坐标;(2)、求 的面积;(3)、若直线 的解析式为 ,则关于 的不等式 的解集为 .23. 生活中,我们经常看到有的窗户上安装着遮阳蓬,如图1,现在要为一个面向正南方向的窗户安装一个矩形遮阳蓬.如图2, 表示窗户的高, 表示遮阳莲,且 ,遮阳莲与窗户所在平面的夹角 等于 .已知该地区冬天正午太阳最低时,光线与水平线的夹角为 ;夏天正午太阳最高时,光线与水平线的夹角为 ,若使冬天正午阳光最低时光线最大限度的射入室内,而夏天正午阳光最高时光线刚好不射入室内,试求出遮阳蓬的宽度 .
(1)、求 , 的坐标;(2)、求 的面积;(3)、若直线 的解析式为 ,则关于 的不等式 的解集为 .23. 生活中,我们经常看到有的窗户上安装着遮阳蓬,如图1,现在要为一个面向正南方向的窗户安装一个矩形遮阳蓬.如图2, 表示窗户的高, 表示遮阳莲,且 ,遮阳莲与窗户所在平面的夹角 等于 .已知该地区冬天正午太阳最低时,光线与水平线的夹角为 ;夏天正午太阳最高时,光线与水平线的夹角为 ,若使冬天正午阳光最低时光线最大限度的射入室内,而夏天正午阳光最高时光线刚好不射入室内,试求出遮阳蓬的宽度 .