山东省临沂市兰陵县2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-04-01 类型:期末考试
一、单选题
-
1. 用配方法解方程 ,方程应变形为( )A、 B、 C、 D、2. 保护环境,人人有责.下列四个图形是生活中常见的垃圾回收标志,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 点 均在二次函数 的图象上,则 的大小关系是( )A、 B、 C、 D、4. 已知二次函数 ,下列说法正确的是( )A、抛物线开口向下 B、当 时, 随 的增大而减小 C、二次函数的最小值是2 D、抛物线的对称轴是直线5. 在“众志成城,共战疫情”党员志愿者进社区服务活动中,小晴和小霞分别从“A,B,C三个社区”中随机选择一个参加活动,两人恰好选择同一社区的概率是( )A、 B、 C、 D、6. 关于反比例函数 ,下列说法中错误的是( )A、当 时, 随 的增大而增大 B、图象位于第二、四象限 C、点 在函数图象上 D、当 时,7. 如图,在给出网格中,小正方形的边长为1,点 , , 都在格点上,则cos A =( )
3. 点 均在二次函数 的图象上,则 的大小关系是( )A、 B、 C、 D、4. 已知二次函数 ,下列说法正确的是( )A、抛物线开口向下 B、当 时, 随 的增大而减小 C、二次函数的最小值是2 D、抛物线的对称轴是直线5. 在“众志成城,共战疫情”党员志愿者进社区服务活动中,小晴和小霞分别从“A,B,C三个社区”中随机选择一个参加活动,两人恰好选择同一社区的概率是( )A、 B、 C、 D、6. 关于反比例函数 ,下列说法中错误的是( )A、当 时, 随 的增大而增大 B、图象位于第二、四象限 C、点 在函数图象上 D、当 时,7. 如图,在给出网格中,小正方形的边长为1,点 , , 都在格点上,则cos A =( ) A、 B、 C、 D、8. 如图,已知 ,它们依次交直线 、 于点 、 、 和点 、 、 ,如果 , ,那么 等于( )
A、 B、 C、 D、8. 如图,已知 ,它们依次交直线 、 于点 、 、 和点 、 、 ,如果 , ,那么 等于( ) A、 B、 C、 D、9. 如图,点A、B、C在⊙O上,若∠A=∠C=35°,则∠B的度数等于( )
A、 B、 C、 D、9. 如图,点A、B、C在⊙O上,若∠A=∠C=35°,则∠B的度数等于( ) A、65° B、70° C、55° D、60°10. 二次函数 ,当 时,则( )A、 B、 C、 D、11. 如图,函数 与 ( )在同一平面直角坐标系中的图像大致( )A、
A、65° B、70° C、55° D、60°10. 二次函数 ,当 时,则( )A、 B、 C、 D、11. 如图,函数 与 ( )在同一平面直角坐标系中的图像大致( )A、 B、
B、 C、
C、 D、
D、 12. △ABC中,∠C=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB,BC分别交于点E,D,则AE的长为( )
12. △ABC中,∠C=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB,BC分别交于点E,D,则AE的长为( ) A、 B、 C、 D、13. 从地面竖直向上抛出一小球,小球的高度 h (单位: m )与小球运动时间 (单位: s )之间的函数关系如图所示.下列结论:
A、 B、 C、 D、13. 从地面竖直向上抛出一小球,小球的高度 h (单位: m )与小球运动时间 (单位: s )之间的函数关系如图所示.下列结论:①小球在空中经过的路程是 40m ;②小球运动的时间为 6s ;③小球抛出3秒时,速度为0;
④当 时,小球的高度 .其中正确的是( )
 A、①④ B、①② C、②③④ D、②④14. 如图,等边△OAB的边OB在 轴上,点B坐标为(2,0),以点O为旋转中心,把△OAB逆时针转90 ,则旋转后点A的对应点 的坐标是( )
A、①④ B、①② C、②③④ D、②④14. 如图,等边△OAB的边OB在 轴上,点B坐标为(2,0),以点O为旋转中心,把△OAB逆时针转90 ,则旋转后点A的对应点 的坐标是( )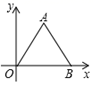 A、(-1, ) B、( ,-1) C、( ) D、(-2,1)
A、(-1, ) B、( ,-1) C、( ) D、(-2,1)二、填空题
-
15. 将一个篮球和一个足球随机放入三个不同的篮子中,则恰有一个篮子为空的概率 .16. 已知二次函数y=x2+2mx+1,当x>1时,y随x的增大而增大,则m的取值范围是17. 如图,⊙O的直径AB=2,C是半圆上任意一点,∠BCD=60°,则劣弧AD的长为 .
 18. 如图,正方形 中, 为 边上一点,且 ,将 绕点 逆时针旋转 得到 ,连接 、 ,则线段 的长度是 .
18. 如图,正方形 中, 为 边上一点,且 ,将 绕点 逆时针旋转 得到 ,连接 、 ,则线段 的长度是 .
三、解答题
-
19. 如图,海中有一小岛 ,它周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在 点测得小岛 在北偏东 方向上,航行12海里到达 点,这时测得小岛 在北偏东 方向上.如果渔船不改变航线继续向东航行,有没有触礁的危险?说明理由.(参考数据: )
 20. 如图, 为 的直径, 为 上一点, 和过点 的切线互相垂直,垂足为 , , 的延长线交于点 .
20. 如图, 为 的直径, 为 上一点, 和过点 的切线互相垂直,垂足为 , , 的延长线交于点 . (1)、求证: 平分 ;(2)、若 , ,求图中阴影部分的面积.
(1)、求证: 平分 ;(2)、若 , ,求图中阴影部分的面积.

