山东省济宁市任城区2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-04-01 类型:期末考试
一、单选题
-
1. 下列四幅图中,能表示两棵树在同一时刻太阳光下的影子的图是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,在 中,∠C=90°,设∠A , ∠B , ∠C所对的边分别为a , b , c , 则( )
2. 如图,在 中,∠C=90°,设∠A , ∠B , ∠C所对的边分别为a , b , c , 则( ) A、c=bsinB B、b=csinB C、a=btanB D、b=ctanB3. 如图, 是⊙O的直径,点C、D在⊙O上, ,则 的大小为( )
A、c=bsinB B、b=csinB C、a=btanB D、b=ctanB3. 如图, 是⊙O的直径,点C、D在⊙O上, ,则 的大小为( )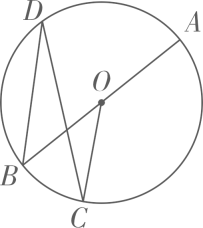 A、 B、 C、 D、4. 如图所示的几何体是由四个完全相同的小正方体搭成的,它的俯视图是( )
A、 B、 C、 D、4. 如图所示的几何体是由四个完全相同的小正方体搭成的,它的俯视图是( )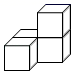 A、
A、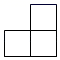 B、
B、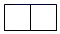 C、
C、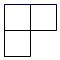 D、
D、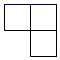 5. 为了解某地区九年级男生的身高情况,随机抽取了该地区1000名九年级男生的身高数据,统计结果如下.
5. 为了解某地区九年级男生的身高情况,随机抽取了该地区1000名九年级男生的身高数据,统计结果如下.身高
人数
60
260
550
130
根据以上统计结果,随机抽取该地区一名九年级男生,估计他的身高不低于 的概率是( )
A、0.32 B、0.55 C、0.68 D、0.876. 下列事件中,是必然事件的是( )A、从一个只有白球的盒子里摸出一个球是白球 B、任意买一张电影票,座位号是3的倍数 C、掷一枚质地均匀的硬币,正面向上 D、汽车走过一个红绿灯路口时,前方正好是绿灯7. 如图所示,过y轴正半轴上的任意一点P , 作x轴的平行线,分别与反比例函数 和 的图象交于点A和点B , 若点C是x轴上任意一点,连接 ,则 的面积为( )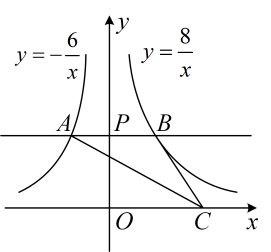 A、6 B、7 C、8 D、148. 如图,正方形 的边长为4,以点A为圆心, 为半径画圆弧 得到扇形 (阴影部分,点E在对角线 上).若扇形 正好是一个圆锥的侧面展开图,则该圆锥的底面圆的半径是( )
A、6 B、7 C、8 D、148. 如图,正方形 的边长为4,以点A为圆心, 为半径画圆弧 得到扇形 (阴影部分,点E在对角线 上).若扇形 正好是一个圆锥的侧面展开图,则该圆锥的底面圆的半径是( ) A、 B、1 C、 D、9. 如图,抛物线y=ax2+bx+4交y轴于点A,交过点A且平行于x轴的直线于另一点B,交x轴于C,D两点(点C在点D右边),对称轴为直线x= ,连接AC,AD,BC.若点B关于直线AC的对称点恰好落在线段OC上,下列结论中错误的是( )
A、 B、1 C、 D、9. 如图,抛物线y=ax2+bx+4交y轴于点A,交过点A且平行于x轴的直线于另一点B,交x轴于C,D两点(点C在点D右边),对称轴为直线x= ,连接AC,AD,BC.若点B关于直线AC的对称点恰好落在线段OC上,下列结论中错误的是( )
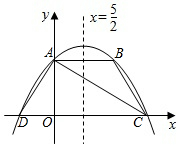 A、点B坐标为(5,4) B、AB=AD C、a= D、OC•OD=1610. 如图, 为半圆O的直径,M,C是半圆上的三等分点, , 与半圆O相切于点B.点P为 上一动点(不与点A,M重合),直线 交 于点D, 于点E,延长 交 于点F,则下列结论正确的个数有( )
A、点B坐标为(5,4) B、AB=AD C、a= D、OC•OD=1610. 如图, 为半圆O的直径,M,C是半圆上的三等分点, , 与半圆O相切于点B.点P为 上一动点(不与点A,M重合),直线 交 于点D, 于点E,延长 交 于点F,则下列结论正确的个数有( )
① ;② 的长为 ;③ ;④ ;⑤ 为定值
A、2个 B、3个 C、4个 D、5个二、填空题
-
11. 一只蚂蚁在如图所示的树枝上寻觅食物,假定蚂蚁在岔路口随机选择一条路径,它获得食物的概率是 。
 12. 如图,工人师傅用扳手拧形状为正六边形的螺帽,现测得扳手的开口宽度 ,则螺帽边长 cm.
12. 如图,工人师傅用扳手拧形状为正六边形的螺帽,现测得扳手的开口宽度 ,则螺帽边长 cm.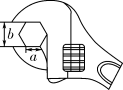 13. 如图是一个几何体的三视图,根据图中所示数据求得这个几何体的侧面积是(结果保留π).
13. 如图是一个几何体的三视图,根据图中所示数据求得这个几何体的侧面积是(结果保留π).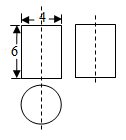 14. 如图,在平面直角坐标系中,点P在第一象限, 与x轴、y轴都相切,且经过矩形 的顶点C,与 相交于点D.若 的半径为5,点A的坐标是 .则点D的坐标是 .
14. 如图,在平面直角坐标系中,点P在第一象限, 与x轴、y轴都相切,且经过矩形 的顶点C,与 相交于点D.若 的半径为5,点A的坐标是 .则点D的坐标是 .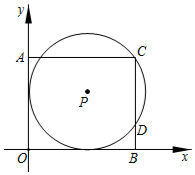 15. 二次函数 的图像过点 ,且与y轴交于点B,点M在该抛物线的对称轴上,若 是以 为直角边的直角三角形,则点M的坐标为.
15. 二次函数 的图像过点 ,且与y轴交于点B,点M在该抛物线的对称轴上,若 是以 为直角边的直角三角形,则点M的坐标为.三、解答题
-
16. 已知抛物线 经过点(1,﹣2),(﹣2,13).(1)、求a , b的值;(2)、若(5, ),(m , )是抛物线上不同的两点,且 ,求m的值.17. 为了学生的安全,某校决定把一段如图所示的步梯路段进行改造.已知四边形 为矩形, ,其坡度为 ,将步梯 改造为斜坡 ,其坡度为 ,求斜坡 的长度.(结果精确到 ,参考数据: , )
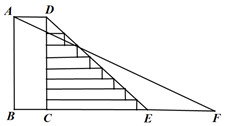 18. 如图,在 中, , , .将 以点B为中心,逆时针旋转,使 边落在 边延长线上.在图上画出直角边 扫过的图形(用阴影表示),并求出它的面积.
18. 如图,在 中, , , .将 以点B为中心,逆时针旋转,使 边落在 边延长线上.在图上画出直角边 扫过的图形(用阴影表示),并求出它的面积. 19. 一个不透明的盒子里装有除颜色外其余均相同的2个黑球和n个白球,搅匀后从盒子里随机摸出一个球,摸到白球的概率为 .(1)、求n的值;(2)、所有球放入盒中,搅匀后随机从中摸出1个球,放回搅匀,再随机摸出第2个球,求两次摸球摸到一个白球和一个黑球的概率,请用画树状图或列表的方法进行说明.20. 如图, 为⊙O的直径, 为⊙O上一点, ,垂足为D, 平分 .
19. 一个不透明的盒子里装有除颜色外其余均相同的2个黑球和n个白球,搅匀后从盒子里随机摸出一个球,摸到白球的概率为 .(1)、求n的值;(2)、所有球放入盒中,搅匀后随机从中摸出1个球,放回搅匀,再随机摸出第2个球,求两次摸球摸到一个白球和一个黑球的概率,请用画树状图或列表的方法进行说明.20. 如图, 为⊙O的直径, 为⊙O上一点, ,垂足为D, 平分 .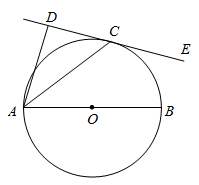 (1)、求证: 是⊙O的切线;(2)、若 , ,求 的长.21. 阅读以下材料,并解决相应问题:
(1)、求证: 是⊙O的切线;(2)、若 , ,求 的长.21. 阅读以下材料,并解决相应问题:小明在课外学习时遇到这样一个问题:
定义:如果二次函数 ( , , 是常数)与 ( , , , 是常数)满足 , , ,则这两个函数互为“旋转函数”.求函数 的旋转函数.小明是这样思考的,由函数 可知, , , ,根据 , , ,求出 , , 就能确定这个函数的旋转函数.
请思考小明的方法解决下面问题:
(1)、写出函数 的旋转函数(2)、若函数 与 互为旋转函数,求 的值.(3)、已知函数 的图象与x轴交于A,B两点,与y轴交于点C,点A,B,C关于原点的对称点分别是 , , ,试求证:经过点 , , 的二次函数与 互为“旋转函数”.22. 如图,已知 , 是 的平分线,A是射线 上一点, .动点P从点A出发,以 的速度沿 水平向左作匀速运动,与此同时,动点Q从点O出发,也以 的速度沿 竖直向上作匀速运动.连接 ,交 于点B.经过O,P,Q三点作圆,交 于点C,连接 , .设运动时间为 ,其中 . (1)、求 的值;(2)、是否存在实数 ,使得线段 的长度最大?若存在,求出t的值;若不存在,说明理由.(3)、在点P,Q运动过程中( ),四边形 的面积是否变化.如果面积变化,请说出四边形 面积变化的趋势;如果四边形 面积不变化,请求出它的面积.
(1)、求 的值;(2)、是否存在实数 ,使得线段 的长度最大?若存在,求出t的值;若不存在,说明理由.(3)、在点P,Q运动过程中( ),四边形 的面积是否变化.如果面积变化,请说出四边形 面积变化的趋势;如果四边形 面积不变化,请求出它的面积.