山东省济南市槐荫区2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2021-04-01 类型:期末考试
一、单选题
-
1. 在Rt△ABC中,∠C=90°,a=5,b=12,则tanB的值为( )A、 B、 C、 D、2. 如图,下列选项中不是正六棱柱的三视图的是( )
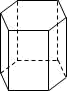 A、
A、 B、
B、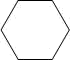 C、
C、 D、
D、 3. 若 ,则 的值是( )A、1 B、2 C、3 D、44. 对于函数 , 下列说法错误的是()A、它的图像分布在一、三象限 B、它的图像既是轴对称图形又是中心对称图形 C、当x>0时,y的值随x的增大而增大 D、当x<0时,y的值随x的增大而减小5. 已知点P是线段AB的黄金分割点(AP>PB),AB=4,那么AP的长是( )A、 B、 C、 D、6. 若二次函数y=﹣x2+bx+c的图象的最高点是(﹣1,﹣3),则b、c的值分别是( )A、b=2,c=4 B、b=﹣2,c=﹣4 C、b=2,c=﹣4 D、b=﹣2,c=47.
3. 若 ,则 的值是( )A、1 B、2 C、3 D、44. 对于函数 , 下列说法错误的是()A、它的图像分布在一、三象限 B、它的图像既是轴对称图形又是中心对称图形 C、当x>0时,y的值随x的增大而增大 D、当x<0时,y的值随x的增大而减小5. 已知点P是线段AB的黄金分割点(AP>PB),AB=4,那么AP的长是( )A、 B、 C、 D、6. 若二次函数y=﹣x2+bx+c的图象的最高点是(﹣1,﹣3),则b、c的值分别是( )A、b=2,c=4 B、b=﹣2,c=﹣4 C、b=2,c=﹣4 D、b=﹣2,c=47.如图,▱ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC等于( )
 A、1:1 B、1:2 C、1:3 D、2:38.
A、1:1 B、1:2 C、1:3 D、2:38.如图,四边形ABCD内接于⊙O,若它的一个外角∠DCE=70°,则∠BOD=( )
 A、35° B、70° C、110° D、140°9. 已知点A(﹣2,y1)、B(a , y2)、C(3,y3)都在双曲线y=﹣ 上,且﹣2<a<0,则( )A、y1<y2<y3 B、y3<y2<y1 C、y3<y1<y2 D、y2<y1<y310. 如图,在菱形 中,点 的坐标为 ,对角线 相交于点 .双曲线 经过点 ,交 的延长线于点 ,则过点 的双曲线表达式为( )
A、35° B、70° C、110° D、140°9. 已知点A(﹣2,y1)、B(a , y2)、C(3,y3)都在双曲线y=﹣ 上,且﹣2<a<0,则( )A、y1<y2<y3 B、y3<y2<y1 C、y3<y1<y2 D、y2<y1<y310. 如图,在菱形 中,点 的坐标为 ,对角线 相交于点 .双曲线 经过点 ,交 的延长线于点 ,则过点 的双曲线表达式为( ) A、 B、 C、 D、11. 如图,在矩形ABCD中,∠ADC的平分线与AB交于E,点F在DE的延长线上,∠BFE=90°,连接AF、CF,CF与AB交于G.有以下结论:①AE=BC②AF=CF③BF2=FG•FC④EG•AE=BG•AB其中正确的个数是( )
A、 B、 C、 D、11. 如图,在矩形ABCD中,∠ADC的平分线与AB交于E,点F在DE的延长线上,∠BFE=90°,连接AF、CF,CF与AB交于G.有以下结论:①AE=BC②AF=CF③BF2=FG•FC④EG•AE=BG•AB其中正确的个数是( )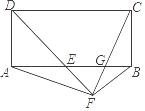 A、1 B、2 C、3 D、412. 如图,将抛物线 的图象位于直线 以上的部分向下翻折,得到新的图象(实线部分),若直线 与新图象只有四个交点,求 的取值范围.( )
A、1 B、2 C、3 D、412. 如图,将抛物线 的图象位于直线 以上的部分向下翻折,得到新的图象(实线部分),若直线 与新图象只有四个交点,求 的取值范围.( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 如图,已知路灯离地面的高度AB为4.8m,身高为1.6m的小明站在D处的影长为2m,那么此时小明离电杆AB的距离BD为m.
 14. 如图,一人乘雪橇沿坡比1:的斜坡笔直滑下72米,那么他下降的高度为 米.
14. 如图,一人乘雪橇沿坡比1:的斜坡笔直滑下72米,那么他下降的高度为 米. 15. 如图,AB是⊙O的直径,C、D是⊙O上的两点,∠AOC=120°,则∠CDB=°.
15. 如图,AB是⊙O的直径,C、D是⊙O上的两点,∠AOC=120°,则∠CDB=°. 16. 二次函数 ,当 时,y的取值范围为 .17. 如图,⊙O的半径为1,点O到直线l的距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为 .
16. 二次函数 ,当 时,y的取值范围为 .17. 如图,⊙O的半径为1,点O到直线l的距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为 . 18. 如图,抛物线 与直线 交于 , 两点,则不等式 的解集是 .
18. 如图,抛物线 与直线 交于 , 两点,则不等式 的解集是 .
三、解答题
-
19. 计算:2sin60°•tan30°+cos230°﹣tan45°.20. 如图,有长为24米的篱笆,一面利用墙(墙的最大可用长度a为15米),围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为x米,面积为S .
 (1)、求S与x的函数关系式;(2)、并求出当AB的长为多少时,花圃的面积最大,最大值是多少?21. 如图,方格纸中的每个小方格都是边长为1的正方形,△ABC的顶点均在格点上.
(1)、求S与x的函数关系式;(2)、并求出当AB的长为多少时,花圃的面积最大,最大值是多少?21. 如图,方格纸中的每个小方格都是边长为1的正方形,△ABC的顶点均在格点上. (1)、以原点O为位似中心,画出△ABC的位似图形,使它与△ABC的相似比是 ;(2)、点C的对应点的坐标为;(3)、∠A的正切值是 .22. 如图,在△ABC中,∠BAC=90°,AB=AC=2,BD=1,DC=2CE . 求证:cos∠ADE= .
(1)、以原点O为位似中心,画出△ABC的位似图形,使它与△ABC的相似比是 ;(2)、点C的对应点的坐标为;(3)、∠A的正切值是 .22. 如图,在△ABC中,∠BAC=90°,AB=AC=2,BD=1,DC=2CE . 求证:cos∠ADE= . 23. 如图,广场上空有一个气球A , 地面上点B、C在一条直线上,BC=24m . 在点B、C分别测得气球A的仰角为30°和60°,求气球A离地面的高度.
23. 如图,广场上空有一个气球A , 地面上点B、C在一条直线上,BC=24m . 在点B、C分别测得气球A的仰角为30°和60°,求气球A离地面的高度. 24. 如图,AB是半圆O的直径,点P是BA延长线上一点,PC是⊙O的切线,切点为C,过点B作BD⊥PC交PC的延长线于点D,连接BC.求证:
24. 如图,AB是半圆O的直径,点P是BA延长线上一点,PC是⊙O的切线,切点为C,过点B作BD⊥PC交PC的延长线于点D,连接BC.求证: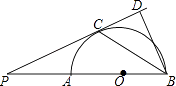 (1)、∠PBC=∠CBD;(2)、BC2=AB•BD.25. 如图,一次函数y=k1x+b的图象与反比例函数y= (x<0)的图象相交于点A(﹣1,2)、点B(﹣4,n).
(1)、∠PBC=∠CBD;(2)、BC2=AB•BD.25. 如图,一次函数y=k1x+b的图象与反比例函数y= (x<0)的图象相交于点A(﹣1,2)、点B(﹣4,n).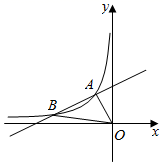 (1)、求此一次函数和反比例函数的表达式;(2)、求△AOB的面积;(3)、若点H(﹣ ,h)也在双曲线上,那么在y轴上存在一点P , 使得|PB﹣PH|的差最大,求出点P的坐标.26. 如图
(1)、求此一次函数和反比例函数的表达式;(2)、求△AOB的面积;(3)、若点H(﹣ ,h)也在双曲线上,那么在y轴上存在一点P , 使得|PB﹣PH|的差最大,求出点P的坐标.26. 如图 (1)、如图1,△ABC和△CDE均为等边三角形,直线AD和直线BE交于点F .
(1)、如图1,△ABC和△CDE均为等边三角形,直线AD和直线BE交于点F .①求证:AD=BE;
②求∠AFB的度数.
(2)、如图2,△ABC和△CDE均为等腰直角三角形,∠ABC=∠DEC=90°,直线AD和直线BE交于点F .①求证:AD= BE;
②若AB=BC=3,DE=EC= .将△CDE绕着点C在平面内旋转,当点D落在线段BC上时,在图3中画出图形,并求BF的长度.
27. 如图,二次函数y=﹣x2+bx+3的图象与x轴交于点A、B , 与y轴交于点C , 点A的坐标为(﹣1,0),点D为OC的中点,点P在抛物线上.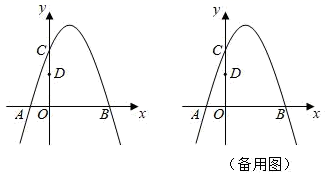 (1)、b=;(2)、若点P在第一象限,过点P作PH⊥x轴,垂足为H , PH与BC、BD分别交于点M、N . 是否存在这样的点P , 使得PM=MN=NH?若存在,求出点P的坐标;若不存在,请说明理由;(3)、若点P的横坐标小于3,过点P作PQ⊥BD , 垂足为Q , 直线PQ与x轴交于点R , 且S△PQB=2S△QRB , 求点P的坐标.
(1)、b=;(2)、若点P在第一象限,过点P作PH⊥x轴,垂足为H , PH与BC、BD分别交于点M、N . 是否存在这样的点P , 使得PM=MN=NH?若存在,求出点P的坐标;若不存在,请说明理由;(3)、若点P的横坐标小于3,过点P作PQ⊥BD , 垂足为Q , 直线PQ与x轴交于点R , 且S△PQB=2S△QRB , 求点P的坐标.