山东省菏泽市定陶区2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-04-01 类型:期末考试
一、单选题
-
1. 下列多边形一定相似的是( )A、两个平行四边形 B、两个矩形 C、两个菱形 D、两个正方形2. 如图,在菱形ABCD中,DE⊥AB,cosA= ,BE=2,则BD的值( )
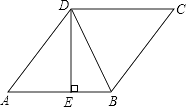 A、2 B、 C、2 D、53. 如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是( )
A、2 B、 C、2 D、53. 如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是( ) A、AC=AB B、∠C= ∠BOD C、∠C=∠B D、∠A=∠B0D4. 、 是实数,点 、 在反比例函数 的图象上.则( )A、 B、 C、 D、5. 如图,在△ABC中,D是边AC上一点,连BD,给出下列条件:①∠ABD=∠ACB;②AB2=AD•AC;③AD•BC=AB•BD;④AB•BC=AC•BD.其中单独能够判定△ABC∽△ADB的个数是( )
A、AC=AB B、∠C= ∠BOD C、∠C=∠B D、∠A=∠B0D4. 、 是实数,点 、 在反比例函数 的图象上.则( )A、 B、 C、 D、5. 如图,在△ABC中,D是边AC上一点,连BD,给出下列条件:①∠ABD=∠ACB;②AB2=AD•AC;③AD•BC=AB•BD;④AB•BC=AC•BD.其中单独能够判定△ABC∽△ADB的个数是( )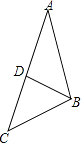 A、①② B、①②③ C、①②④ D、①②③④6. 已知方程x2﹣7x+10=0的两个根是等腰三角形的两边长,则这个等腰三角形的周长为( )A、9 B、12 C、12或9 D、不能确定7. 如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4,BD为⊙O的直径,则BD等于( )
A、①② B、①②③ C、①②④ D、①②③④6. 已知方程x2﹣7x+10=0的两个根是等腰三角形的两边长,则这个等腰三角形的周长为( )A、9 B、12 C、12或9 D、不能确定7. 如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4,BD为⊙O的直径,则BD等于( )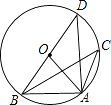 A、4 B、6 C、8 D、128. 关于 的一元二次方程 的根的情况是( )A、无法确定 B、有两个不相等的实数根 C、有两个相等的实数根 D、无实数根9. 某超市1月份营业额为90万元,1月、2月、3月总营业额为144万元,设平均每月营业额增长率为x , 则下面所列方程正确的是( )A、90(1+x)2=144 B、90(1-x)2=144 C、90(1+2x)=144 D、90(1+x)+90(1+x)2=144-9010. 关于 的一元二次方程 没有实数根,则整数 的最小值是( )A、0 B、1 C、2 D、3
A、4 B、6 C、8 D、128. 关于 的一元二次方程 的根的情况是( )A、无法确定 B、有两个不相等的实数根 C、有两个相等的实数根 D、无实数根9. 某超市1月份营业额为90万元,1月、2月、3月总营业额为144万元,设平均每月营业额增长率为x , 则下面所列方程正确的是( )A、90(1+x)2=144 B、90(1-x)2=144 C、90(1+2x)=144 D、90(1+x)+90(1+x)2=144-9010. 关于 的一元二次方程 没有实数根,则整数 的最小值是( )A、0 B、1 C、2 D、3二、填空题
-
11. .12. 已知y与x成反比例,且当x=-3时,y=4,则当x=6时,y的值为.13. 关于 x 的方程 x2+5x+m=0 的一个根为﹣2,则另一个根是 .14. 抛物线y=(x﹣1)2﹣1的顶点在直线y=kx﹣3上,则k= .15. 如图,⊙O是△ABC的内切圆,切点分别为D、E、F,∠A=80°,点P为⊙O上任意一点(不与E、F重合),则∠EPF= .
 16. 如图,五一黄金周期间,某景区规定 和 为入口, , , 为出口,小红随机选一个入口进入景区,游玩后任选一个出口离开,则她选择从 入口进入、从 , 出口离开的概率是 .
16. 如图,五一黄金周期间,某景区规定 和 为入口, , , 为出口,小红随机选一个入口进入景区,游玩后任选一个出口离开,则她选择从 入口进入、从 , 出口离开的概率是 .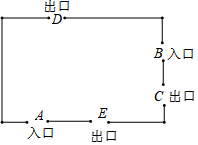 17. 如图, 是反比例函数 图象上的一点,过点 作 轴于点 ,点 在 轴上, 的面积为1,则 的值为 .
17. 如图, 是反比例函数 图象上的一点,过点 作 轴于点 ,点 在 轴上, 的面积为1,则 的值为 .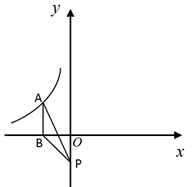 18. 如图,直线x=2与反比例函数 和 的图象分别交于A、B两点,若点P是y轴上任意一点,则△PAB的面积是 .
18. 如图,直线x=2与反比例函数 和 的图象分别交于A、B两点,若点P是y轴上任意一点,则△PAB的面积是 .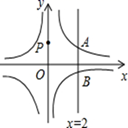
三、解答题
-
19. 解方程(1)、 ;(2)、 .20. 小明、小林是某中学九年级的同班同学.在三月份举行的自主招生考试中,他俩都被同一所高中提前录取,并被编入A,B,C三个班,他俩希望能两次成为同班同学.(1)、请你用画树状图法或列举法,列出所有可能的结果;
(2)、求两人两次成为同班同学的概率.21. 已知:如图, 中, , 是中线, 是 上一点,过 作 ,延长 交 于 ,交 于 .求证: . 22. 如图,小明在M处用高1米(DM=1米)的测角仪测得旗杆AB的顶端B的仰角为30°,再向旗杆方向前进10米到F处,又测得旗杆顶端B的仰角为60°,请求出旗杆AB的高度(取 ≈1.73,结果保留整数)
22. 如图,小明在M处用高1米(DM=1米)的测角仪测得旗杆AB的顶端B的仰角为30°,再向旗杆方向前进10米到F处,又测得旗杆顶端B的仰角为60°,请求出旗杆AB的高度(取 ≈1.73,结果保留整数)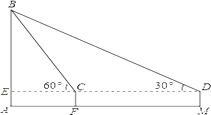 23. 如图, 是 的直径,弦 与点 ,点 在 上, .
23. 如图, 是 的直径,弦 与点 ,点 在 上, .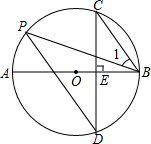 (1)、求证: ;(2)、若 , ,求 的长.24. 如图在平面直角坐标系 中,一次函数 的图象与反比例函数 的图象交于第二、四象限内的 、 两点,与 轴交于 点,点 的坐标为 .线段 , 为 轴上一点,且 .
(1)、求证: ;(2)、若 , ,求 的长.24. 如图在平面直角坐标系 中,一次函数 的图象与反比例函数 的图象交于第二、四象限内的 、 两点,与 轴交于 点,点 的坐标为 .线段 , 为 轴上一点,且 .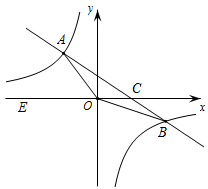 (1)、求该反比例函数和一次函数的解析式;(2)、求 的面积;25. 某商店经销一种健身球,已知这种健身球的成本价为每个20元,市场调查发现,该种健身球每天的销售量y(个)与销售单价x(元)有如下关系:y=﹣2x+80(20≤x≤40).设这种健身球每天的销售利润为W元.(1)、求W与x之间的函数关系式;(2)、该种健身球销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?26. 如图1,在平面直角坐标系 中,抛物线 与 轴交于 、 两点,其中 ,与 轴交于点 ,点 是 轴上方的抛物线上一动点(不与点 重合).
(1)、求该反比例函数和一次函数的解析式;(2)、求 的面积;25. 某商店经销一种健身球,已知这种健身球的成本价为每个20元,市场调查发现,该种健身球每天的销售量y(个)与销售单价x(元)有如下关系:y=﹣2x+80(20≤x≤40).设这种健身球每天的销售利润为W元.(1)、求W与x之间的函数关系式;(2)、该种健身球销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?26. 如图1,在平面直角坐标系 中,抛物线 与 轴交于 、 两点,其中 ,与 轴交于点 ,点 是 轴上方的抛物线上一动点(不与点 重合).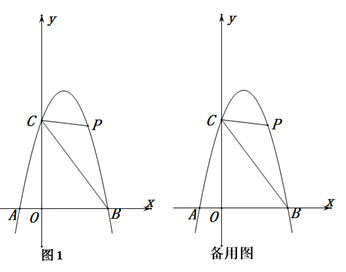 (1)、求抛物线的表达式;(2)、过点 作 轴于点 ,交直线 于点 ,点 关于直线 的对称点为 ,若点 落在 轴上(不与点 重合).请判断以 , , , 为顶点的四边形的形状,并说明理由;(3)、在(2)的条件下直接写出点 的坐标.
(1)、求抛物线的表达式;(2)、过点 作 轴于点 ,交直线 于点 ,点 关于直线 的对称点为 ,若点 落在 轴上(不与点 重合).请判断以 , , , 为顶点的四边形的形状,并说明理由;(3)、在(2)的条件下直接写出点 的坐标.