山东省德州市齐河县2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-04-01 类型:期末考试
一、单选题
-
1. 下面四个图案既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图是由几个相同大小的小正方体搭建而成的几何体的主视图和俯视图视图,则搭建这个几何体所需要的小正方体的个数至少为( )
2. 如图是由几个相同大小的小正方体搭建而成的几何体的主视图和俯视图视图,则搭建这个几何体所需要的小正方体的个数至少为( ) A、5 B、6 C、7 D、83. 如图,已知⊙O的半径为4,M是⊙O内一点,且OM=2,则过点M的所有弦中,弦长是整数的共有( )
A、5 B、6 C、7 D、83. 如图,已知⊙O的半径为4,M是⊙O内一点,且OM=2,则过点M的所有弦中,弦长是整数的共有( ) A、1条 B、2条 C、3条 D、4条4. 如图,已知 OAB是正三角形,OP⊥OB , OP=OA , 将 OAB绕点O按顺时针方向旋转,使得OA与OP重合,得到 OPQ , 则旋转的角度是( )
A、1条 B、2条 C、3条 D、4条4. 如图,已知 OAB是正三角形,OP⊥OB , OP=OA , 将 OAB绕点O按顺时针方向旋转,使得OA与OP重合,得到 OPQ , 则旋转的角度是( ) A、60° B、90° C、120° D、150°5. 如图,在一张正六边形纸片中剪下两个全等的直角三角形(阴影部分),拼成一个四边形,若拼成的四边形的周长为12,则纸片的剩余部分拼成的五边形的面积为( )
A、60° B、90° C、120° D、150°5. 如图,在一张正六边形纸片中剪下两个全等的直角三角形(阴影部分),拼成一个四边形,若拼成的四边形的周长为12,则纸片的剩余部分拼成的五边形的面积为( ) A、24 B、20 C、8 D、166. 如图,在△ABC中,∠C=90°,AC=32,AB的垂直平分线MN交AC于点D , 连接BD , 若sin∠CBD= ,则BC的长是( )
A、24 B、20 C、8 D、166. 如图,在△ABC中,∠C=90°,AC=32,AB的垂直平分线MN交AC于点D , 连接BD , 若sin∠CBD= ,则BC的长是( ) A、16 B、8 C、4 D、87. 如图是二次函数y=mx2+nx+k图象的一部分且过点P(3,0),二次函数图象的对称轴是直线x=1,下列结论正确的是( )
A、16 B、8 C、4 D、87. 如图是二次函数y=mx2+nx+k图象的一部分且过点P(3,0),二次函数图象的对称轴是直线x=1,下列结论正确的是( ) A、n2﹣4mk<0 B、mk>0 C、n=2m D、m﹣n+k=08. “学雷锋”活动月中,“飞翼”班将组织学生开展志愿者服务活动,小晴和小霞从“图书馆,博物馆,科技馆”三个场馆中随机选择一个参加活动,两人恰好选择同一场馆的概率是( )A、 B、 C、 D、9. 今年由于受新型冠状病毒的影响,一次性医用口罩的销量剧增.某药店一月份销售量是5000枚,二、三两个月销售量连续增长.若月平均增长率为x , 则该药店三月份销售口罩枚数y(枚)与x的函数关系式是( )A、y=5000(1+x) B、y=5000(1+x)2 C、y=5000(1+x2) D、y=5000(1+2x)10. 如图,四边形AOBC和四边形CDEF都是正方形,边OA在y轴上,边OB在x轴上,点F在边AC上,反比例函数y= 在第一象限的图象经过点E , 则正方形AOBC和正方形CDEF的面积之差为( )
A、n2﹣4mk<0 B、mk>0 C、n=2m D、m﹣n+k=08. “学雷锋”活动月中,“飞翼”班将组织学生开展志愿者服务活动,小晴和小霞从“图书馆,博物馆,科技馆”三个场馆中随机选择一个参加活动,两人恰好选择同一场馆的概率是( )A、 B、 C、 D、9. 今年由于受新型冠状病毒的影响,一次性医用口罩的销量剧增.某药店一月份销售量是5000枚,二、三两个月销售量连续增长.若月平均增长率为x , 则该药店三月份销售口罩枚数y(枚)与x的函数关系式是( )A、y=5000(1+x) B、y=5000(1+x)2 C、y=5000(1+x2) D、y=5000(1+2x)10. 如图,四边形AOBC和四边形CDEF都是正方形,边OA在y轴上,边OB在x轴上,点F在边AC上,反比例函数y= 在第一象限的图象经过点E , 则正方形AOBC和正方形CDEF的面积之差为( ) A、12 B、10 C、6 D、4
A、12 B、10 C、6 D、4二、填空题
-
11. 已知关于x的一元二次方程nx2﹣2x+1=0有实数根,则n的取值范围是 .12. 在Rt△ABC中,∠C=90°,AB=17,BC=8,则sinB= .13. 一个直角三角形的两条边分别为4和8,另一个直角三角形的两条边分别为3和6,那么这两个直角三角形(选填“一定”“不一定”或“一定不”)相似.14. 如图,在平行四边形MNPQ中,点E是NP边的中点,连接ME交对角线NQ于点O , 则△MNO与四边形EPQO的面积之比为 .
 15. 如图,在平面直角坐标系中,菱形ABCD在第二象限内,边AD与x轴平行,A , B两点的横坐标分别为﹣3,﹣1,反比例函数y=﹣ 的图象经过A , B两点,则菱形ABCD的边长为 .
15. 如图,在平面直角坐标系中,菱形ABCD在第二象限内,边AD与x轴平行,A , B两点的横坐标分别为﹣3,﹣1,反比例函数y=﹣ 的图象经过A , B两点,则菱形ABCD的边长为 .
三、解答题
-
16. 用适当的方法解方程:(1)、x2﹣3x﹣4=0;(2)、3x(x﹣1)=2(1﹣x).17. 如图,某学校有一块面积为84m2的矩形空地,准备进行绿化.计划在空地的中间修建两个相同的正方形花坛,其余地方铺草坪,两个花坛之间及与四周的距离均为2m , 求正方形花坛的边长.
 18.
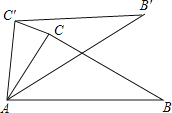
18.如图,在△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB , 求∠BAB′的度数.
 19. 在平面直角坐标系xOy中,二次函数y=ax2+2x﹣3a(a≠0)交x轴于A、B两点(点A在点B的左侧),且抛物线的对称轴为直线x=﹣1.(1)、求此抛物线的解析式及A、B两点坐标;(2)、若抛物线交y轴于点C , 顶点为D , 求四边形ABCD的面积.20. 春节期间,北京为海内外游客奉上了一场“大中国、老北京、最正宗、最有味、最幸福”的节日盛宴.“中国年”成为春节期间年味儿最浓、关注度最高、点赞率最多的热点和亮点.现有5张分别标有:“大中国”、“老北京”、“最正宗”、“最有味”、“最幸福”的卡片,它们除所标文字外质地、大小完全相同.(1)、把卡片背面向上洗匀,从中随机抽取一张,求恰好抽到的卡片上含有“最”字的概率;(2)、把卡片背面向上洗匀,从中随机连续抽取两张,嘉琪说两张卡片上都含有“最”字的概率和(1)中的结果一样,你同意她的观点吗?通过树状图或列表说明.21. 如图,以△PMN的边MN为直径作⊙O , 点P在⊙O上,点Q在线段MN的延长线上,PM=PQ , ∠Q=30°.
19. 在平面直角坐标系xOy中,二次函数y=ax2+2x﹣3a(a≠0)交x轴于A、B两点(点A在点B的左侧),且抛物线的对称轴为直线x=﹣1.(1)、求此抛物线的解析式及A、B两点坐标;(2)、若抛物线交y轴于点C , 顶点为D , 求四边形ABCD的面积.20. 春节期间,北京为海内外游客奉上了一场“大中国、老北京、最正宗、最有味、最幸福”的节日盛宴.“中国年”成为春节期间年味儿最浓、关注度最高、点赞率最多的热点和亮点.现有5张分别标有:“大中国”、“老北京”、“最正宗”、“最有味”、“最幸福”的卡片,它们除所标文字外质地、大小完全相同.(1)、把卡片背面向上洗匀,从中随机抽取一张,求恰好抽到的卡片上含有“最”字的概率;(2)、把卡片背面向上洗匀,从中随机连续抽取两张,嘉琪说两张卡片上都含有“最”字的概率和(1)中的结果一样,你同意她的观点吗?通过树状图或列表说明.21. 如图,以△PMN的边MN为直径作⊙O , 点P在⊙O上,点Q在线段MN的延长线上,PM=PQ , ∠Q=30°. (1)、求证:直线PQ是⊙O的切线;(2)、若直径MN=8,求图中阴影部分的面积.22. 如图,一次函数y=kx+b(k≠0)与反比例函数y= 的图象的一支相交于点A , 与x轴交于点B(﹣1,0),与y轴交于点C , 已知AC=2BC .
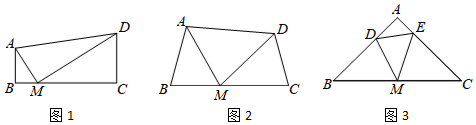
(1)、求证:直线PQ是⊙O的切线;(2)、若直径MN=8,求图中阴影部分的面积.22. 如图,一次函数y=kx+b(k≠0)与反比例函数y= 的图象的一支相交于点A , 与x轴交于点B(﹣1,0),与y轴交于点C , 已知AC=2BC . (1)、求一次函数的解析式;(2)、若反比例函数y= 第一象限上有一点M , MN垂直于x轴,垂足为N , 若△BOC∽△MNB , 求点N的坐标.23.(1)、体验:如图1,在四边形ABCD中,AB∥CD , ∠B=90°,点M在BC边上,当∠AMD=90°时,可知△ABM△MCD(不要求证明).(2)、探究:如图2,在四边形ABCD中,点M在BC上,当∠B=∠C=∠AMD时,求证:△ABM∽△MCD .
(1)、求一次函数的解析式;(2)、若反比例函数y= 第一象限上有一点M , MN垂直于x轴,垂足为N , 若△BOC∽△MNB , 求点N的坐标.23.(1)、体验:如图1,在四边形ABCD中,AB∥CD , ∠B=90°,点M在BC边上,当∠AMD=90°时,可知△ABM△MCD(不要求证明).(2)、探究:如图2,在四边形ABCD中,点M在BC上,当∠B=∠C=∠AMD时,求证:△ABM∽△MCD .拓展:如图3,在△ABC中,点M是边BC的中点,点D、E分别在边AB、AC上.若∠B=∠C=∠DME=45°,BC=8 ,CE=6,求DE的长.