江西省吉安市吉水县2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-04-01 类型：期末考试

进入出卷网下载

一、单选题

1. 点（6，﹣3）是反比例函数y＝ $\frac{k}{x}$ 的图象上的一点，则k＝（）

A、 $- \frac{3}{6}$ B、 $- \frac{6}{3}$ C、﹣18 D、18

查看试题解析
2. 已知a ， b是一元二次方程x²+x﹣3＝0的两根，则a+b﹣2ab等于（）

A、7 B、﹣5 C、﹣7 D、5

查看试题解析

3. 在一个不透明的口袋里，装有仅颜色不同的黑球、白球若干个，某小组做摸球实验：将球搅匀后从中随机摸出一个，记下颜色，再放入袋中，不断重复，下表是活动中的一组数据，则摸到黑球的概率约是（）

摸球的次数n	100	150	200	500	800	1000
摸到黑球的次数m	42	54	84	205	328	401
摸到黑球的频率	0.42	0.3	0.42	0.41	0.41	0.401

A、0.4 B、0.5 C、0.6 D、0.7

查看试题解析

4. 如图，矩形ABCD的对角线AC，BD相交于点O，CE∥BD，DE∥AC，若AC=6cm，则四边形CODE的周长为（）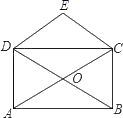

A、6 B、8 C、10 D、12

查看试题解析
5. 如图， $△ A B C$ 中，A，B两个顶点在x轴的上方，点C的坐标是 $(- 1 ， 0) .$ 以点C为位似中心，在x轴的下方作 $△ A B C$ 的位似图形 $△ A' B' C$ ，并把 $△ A B C$ 的边长放大到原来的2倍.设点B的对应点 $B'$ 的横坐标是a，则点B的横坐标是（）

A、 $- \frac{1}{2} a$ B、 $- \frac{1}{2} (a + 1)$ C、 $- \frac{1}{2} (a - 1)$ D、 $- \frac{1}{2} (a + 3)$

查看试题解析
6. 王华晚上由路灯 $A$ 下的 $B$ 处走到 $C$ 处时，测得影子 $C D$ 的长为 $1 m$ ，继续往前走 $3 m$ 到达 $E$ 处时，测得影子 $E F$ 的长为 $2 m$ ，他的身高是 $1.5 m$ ，那么路灯 $A$ 的高度 $A B =$ （）

A、 $8 m$ B、 $7.2 m$ C、 $6 m$ D、 $4.5 m$

查看试题解析

二、填空题

7. 若关于x的一元二次方程ax²+bx﹣7＝0的一个根是x＝1，则2028﹣a﹣b＝．

查看试题解析
8. 在一个不透明的口袋中，有3个完全相同的小球，他们的标号分别是2，3，4，从袋中随机地摸取一个小球然后放回，再随机的摸取一个小球，则两次摸取的小球标号之和为5的概率是．

查看试题解析
9. 美是一种感觉，当人体下半身身长与身高的比值越接近 $\frac{\sqrt{5} - 1}{2}$ （约为0.618）时，越给人一种美感．如图，某女士身高165cm，下半身身长x与身高l的比值是0.60，为尽可能达到好的效果，她应穿的高跟鞋的高度大约为 cm．

查看试题解析
10. 如图，面积为3的矩形OABC的一个顶点B在反比例函数 $y = \frac{k}{x}$ 的图象上，另三点在坐标轴上，则 $k =$ .

查看试题解析
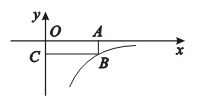11. 如图，正方形ABCD的边长为8，点E为边BC的中点，点P在对角线BD上移动，则PE+PC的最小值是．

查看试题解析
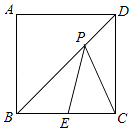12. 如图示意图，A点的坐标为（2，2），点C在线段OA上运动（点C不与O、A重合），过点C作CD⊥x轴于D，再以CD为一边在CD右侧画正方形CDEF．连接AF并延长交x轴于B，连接OF．若△BEF与△OEF相似，则点B的坐标是．

查看试题解析

三、解答题

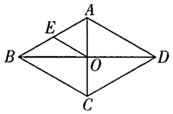
13. 解方程：x²﹣6x﹣7=0．

查看试题解析
14. 如图，菱形 $A B C D$ 中，对角线AC，BD相交于点O，E为AB的中点，若菱形ABCD的周长为32，求OE的长．

查看试题解析
15. 如图，在平面直角坐标系中，点A ， B是一次函数和反比例函数图象的两个交点，请仅用无刻度直尺完成以下作图（保留作图痕迹）．

(1)、在图①中，画出一个平行四边形，使点A ， B都是该平行四边形的顶点；

(2)、在图②中，画出一个菱形，使点A在该菱形一边所在的直线上．

查看试题解析
16. 已知关于x的一元二次方程 $x^{2} + 2 x - k = 0$ 有两个不相等的实数根.

(1)、求k的取值范围；

(2)、若方程的两个不相等实数根是a，b，求 $\frac{a}{a + 1} - \frac{1}{b + 1}$ 的值.

查看试题解析
17. 现如今，“垃圾分类”意识已深入人心，如图是生活中的四个不同的垃圾分类投放桶，分别写着：有害垃圾、易腐垃圾、其他垃圾、可回收垃圾．其中小明投放了一袋垃圾，小丽投放了两袋垃圾．

(1)、直接写出小明投放的垃圾恰好是“易腐垃圾”的概率；

(2)、求小丽投放的两袋垃圾不同类的概率（画树状图或列表求解）

查看试题解析
18. 如图

(1)、如图是一个组合几何体的两种视图，请写出这个组合几何体是由哪两种几何体组成的；

(2)、根据两种视图中尺寸（单位：cm），计算这个组合几何体的体积．（结果保留π）

查看试题解析
19. 如图，将平行四边形ABCD的边DC延长至点E，使CE=DC，连接AE，交BC于点F．

(1)、求证：△ABF≌△ECF；

(2)、连接AC、BE，则当∠AFC与∠D满足什么条件时，四边形ABEC是矩形？请说明理由．

查看试题解析

20. 某工艺品厂设计了一款每件成本为11元的工艺品投放市场进行试销，经过市场调查，得出每天销售量y（件）是每件售价x（元）（x为正整数）的一次函数，其部分对应数据如下表所示：

(1)、求y关于x的函数解析式．

(2)、该工艺品每件售价为多少元时，工艺品厂试销该工艺品每天获得的利润是900元？

每件售价x/元	…	15	16	17	18	…
每天销售量y/件	…	150	140	130	120	…

查看试题解析

21. 如图，在平面直角坐标系中，菱形OABC与菱形ADEF在第一象限，且边OA ， AD在x轴上．反比例函y＝ $\frac{k}{x}$ （x＞0）的图象经过边OC的中点M与边AF的中点N ，已知菱形OABC的边长为4，且∠AOC＝60°．

(1)、求反比例函数的解析式；

(2)、求菱形ADEF的周长．

查看试题解析
22. 方方驾驶小汽车匀速地从A地行驶到B地，行驶里程为480千米，设小汽车的行驶时间为t（单位：小时），行驶速度为v（单位：千米/小时），且全程速度限定为不超过120千米/小时.

(1)、求v关于t的函数表达式；

(2)、方方上午8点驾驶小汽车从A出发.
①方方需在当天12点48分至14点（含12点48分和14点）间到达B地，求小汽车行驶速度v的范围.

②方方能否在当天11点30分前到达B地？说明理由.

查看试题解析
23. 如图，在△ABC中，点D ， E ， F分别在AB ， BC ， AC边上，DE∥AC ， EF∥AB ．

(1)、求证：△BDE∽△EFC；

(2)、设 $\frac{A F}{F C} = \frac{1}{2}$ ．
①若BC＝20，求线段BE的长；

②若△EFC的面积是36，求△ABC的面积．

查看试题解析
24. 如图1，边长为4的正方形ABCD与边长为a（1＜a＜4）的正方形CFEG的顶点C重合，点E在对角线AC上．

(1)、问题发现：

如图1，AE与BF的数量关系为．

(2)、类比探究：
如图2，将正方形CFEG绕点C旋转α度（0＜α＜30），请问（1）中的结论是否仍成立？若成立，写出证明过程；若不成立，请说明理由．

拓展延伸：

(3)、若点F为BC的中点，在正方形CFEG的旋转过程中，当点A ， F ， G在一条直线上时，求线段AG的长度．

查看试题解析