江西省吉安市吉安县2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-04-01 类型:期末考试
一、单选题
-
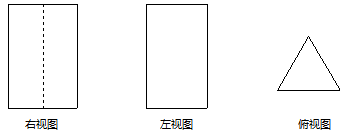
1. 方程 的解是( )A、 B、 C、 , D、 ,2. 如果某物体的三视图是如图所示的三个图形,
那么该物体的形状是( )
A、正方体 B、长方体 C、三棱柱 D、圆锥3. 顺次连接矩形 各边的中点,所得四边形是( )A、平行四边形 B、正方形 C、矩形 D、菱形4. 两个相似多边形的周长比是3:4,其中小多边形的面积为18cm2 , 则较大多边形的面积为( ).A、16cm2 B、54cm2 C、32cm2 D、48cm25. 如图已知双曲线 上有一点 ,过A作AB垂直x轴于点B,连接OA,则 的面积为( ) A、1 B、2 C、3 D、66. 在矩形ABCD中,AB=2,AD=4,E为CD的中点,连接AE交BC的延长线于F点,P为BC上一点,当∠PAE=∠DAE时,AP的长为( )
A、1 B、2 C、3 D、66. 在矩形ABCD中,AB=2,AD=4,E为CD的中点,连接AE交BC的延长线于F点,P为BC上一点,当∠PAE=∠DAE时,AP的长为( )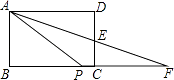 A、4 B、 C、 D、5
A、4 B、 C、 D、5二、填空题
-
7. 反比例函数 的图象在一、三象限,则 应满足 .8. 随机掷一枚均匀的硬币两次,至少有一次正面朝上的概率是 .9. 如图, 中,对角线 长为 , , 长为 ,则 的面积是.
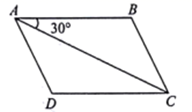 10. 已知菱形的边长为6,一个内角为60°,则菱形较短的对角线长是11. 已知一元二次方程 有一个根为0,则a的值为.12. 在平面直角坐标系中已知点 , ,以原点 为位似中心,相似比为1:2,将 扩大,则点 的对应点 的坐标是 .
10. 已知菱形的边长为6,一个内角为60°,则菱形较短的对角线长是11. 已知一元二次方程 有一个根为0,则a的值为.12. 在平面直角坐标系中已知点 , ,以原点 为位似中心,相似比为1:2,将 扩大,则点 的对应点 的坐标是 .三、解答题
-
13. 解方程:(1)、(2)、14. 如图1,将正方形纸片 对折,使 与 重合,折痕为 如图2,展开后再折叠一次,使点 与点 重合,折痕为 ,点 的对应点为点 , 交 于 ,若 ,则 的长是多少?
 15.
15.在四张背面完全相同的纸牌A、B、C、D,其中正面分别画有四个不同的几何图形(如图),小华将这4张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸一张.
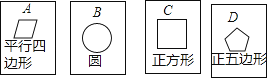 (1)、用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A、B、C、D表示);(2)、求摸出两张纸牌牌面上所画几何图形,既是轴对称图形又是中心对称图形的概率.16. 如图,在平行四边形 中,对角线 与 相交于点 , 是等边三角形, ,求 的面积.
(1)、用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A、B、C、D表示);(2)、求摸出两张纸牌牌面上所画几何图形,既是轴对称图形又是中心对称图形的概率.16. 如图,在平行四边形 中,对角线 与 相交于点 , 是等边三角形, ,求 的面积. 17. 已知方程 的一个根比另一个根小4,求这两个根和 的值.18. 如图,已知点 在 的 边上, 交 于 , 交 于 .
17. 已知方程 的一个根比另一个根小4,求这两个根和 的值.18. 如图,已知点 在 的 边上, 交 于 , 交 于 .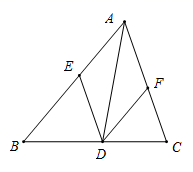 (1)、求证: ;(2)、若 平分 ,试判断四边形 的形状,并说明理由.19. 如图, 与双曲线 交于点 ,与 轴交于点 .
(1)、求证: ;(2)、若 平分 ,试判断四边形 的形状,并说明理由.19. 如图, 与双曲线 交于点 ,与 轴交于点 .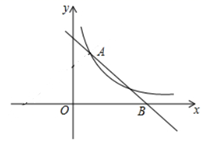 (1)、求双曲线的函数表达式;(2)、直接写出当 时,不等式 的解集.20. 晚上,小亮在广场乘凉,图中线段 表示站立在广场上的小亮,线段 表示直立在广场上的灯杆,点 表示照明灯.
(1)、求双曲线的函数表达式;(2)、直接写出当 时,不等式 的解集.20. 晚上,小亮在广场乘凉,图中线段 表示站立在广场上的小亮,线段 表示直立在广场上的灯杆,点 表示照明灯.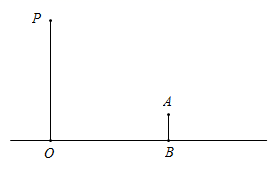 (1)、请你在图中画出小亮在照明灯 照射下的影子 (请保留作图痕迹,并把影子描成粗线);(2)、如果小亮的身高 ,测得小亮影长 ,小亮与灯杆的距离 ,请求出灯杆的高 .21. 文文以0.2元/支的价格购进一批铅笔,以0.4元/支的价格售出,每天销售量为400支,销售了两天后他决定降价,尽早销售完毕经调查得知铅笔单价每降0.01元,每天的销售量增加20支.(1)、为了使笔每天的利润达到原利润的75%,文文应把铅笔定价多少元合适?(2)、如果这批铅笔恰好一共在五天内全部销售完毕,请问这批铅笔有多少支?22. 阅读下面材料,再回答问题:有一些几何图形可以被某条直线分成面积相等的两部分,我们将“把一个几何图形分成面积相等的两部分的直线叫做该图形的二分线”,如:圆的直径所在的直线是圆的“二分线”,正方形的对角线所在的直线是正方形的“二分线”.
(1)、请你在图中画出小亮在照明灯 照射下的影子 (请保留作图痕迹,并把影子描成粗线);(2)、如果小亮的身高 ,测得小亮影长 ,小亮与灯杆的距离 ,请求出灯杆的高 .21. 文文以0.2元/支的价格购进一批铅笔,以0.4元/支的价格售出,每天销售量为400支,销售了两天后他决定降价,尽早销售完毕经调查得知铅笔单价每降0.01元,每天的销售量增加20支.(1)、为了使笔每天的利润达到原利润的75%,文文应把铅笔定价多少元合适?(2)、如果这批铅笔恰好一共在五天内全部销售完毕,请问这批铅笔有多少支?22. 阅读下面材料,再回答问题:有一些几何图形可以被某条直线分成面积相等的两部分,我们将“把一个几何图形分成面积相等的两部分的直线叫做该图形的二分线”,如:圆的直径所在的直线是圆的“二分线”,正方形的对角线所在的直线是正方形的“二分线”.解决下列问题:
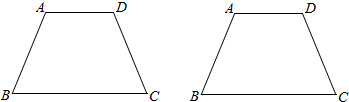 (1)、菱形的“二分线”可以是 .(2)、三角形的“二分线”可以是 .(3)、在下图中,试用两种不同的方法分别画出等腰梯形ABCD的“二分线”.23. 正方形 的边长为4, 是 上的一个动点,过点 作 ,交 的延长线于点 , 交对角线 所在的直线于点 , 交 于点 .
(1)、菱形的“二分线”可以是 .(2)、三角形的“二分线”可以是 .(3)、在下图中,试用两种不同的方法分别画出等腰梯形ABCD的“二分线”.23. 正方形 的边长为4, 是 上的一个动点,过点 作 ,交 的延长线于点 , 交对角线 所在的直线于点 , 交 于点 .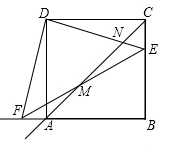 (1)、求证: ;(2)、设 ,当 为何值时, 的面积为1;(3)、随着点 在射线 上的运动, 的值是否会发生变化?若不变,请求出 的值,若变化,请说明理由.
(1)、求证: ;(2)、设 ,当 为何值时, 的面积为1;(3)、随着点 在射线 上的运动, 的值是否会发生变化?若不变,请求出 的值,若变化,请说明理由.