江西省赣州市于都县2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-04-01 类型:期末考试
一、单选题
-
1. 下列图标中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列事件是必然事件的是( )A、实心铁球放入贡江水中,会下沉 B、网上随机购一张电影票,座位号是奇数 C、打开电视机,正播放“农民丰收节”的新闻 D、任意画一个三角形,其内角和为360°3. 如图, 是 的直径, 为圆内一点,则下列说法中正确的是( )
2. 下列事件是必然事件的是( )A、实心铁球放入贡江水中,会下沉 B、网上随机购一张电影票,座位号是奇数 C、打开电视机,正播放“农民丰收节”的新闻 D、任意画一个三角形,其内角和为360°3. 如图, 是 的直径, 为圆内一点,则下列说法中正确的是( ) A、 是 的弦 B、 是圆心角 C、 是圆周角 D、4. 如图,在 中, , ,求证: .当用反证法证明时,第一步应假设( )
A、 是 的弦 B、 是圆心角 C、 是圆周角 D、4. 如图,在 中, , ,求证: .当用反证法证明时,第一步应假设( ) A、 B、 C、 D、5. 受新冠肺炎疫情影响,某企业生产总值从六月份的500万元,连续两个月降至380万元,设平均下降率为x,则可列方程( )A、 B、 C、 D、6. 某数学兴趣小组对我县祁禄山的红军小道的长度进行 次测量,得到 个结果 , , ,…, (单位: ).如果用 作为这条路线长度的近似值,要使得 的值最小, 应选取这 次测量结果的( )A、中位数 B、众数 C、平均数 D、最小值
A、 B、 C、 D、5. 受新冠肺炎疫情影响,某企业生产总值从六月份的500万元,连续两个月降至380万元,设平均下降率为x,则可列方程( )A、 B、 C、 D、6. 某数学兴趣小组对我县祁禄山的红军小道的长度进行 次测量,得到 个结果 , , ,…, (单位: ).如果用 作为这条路线长度的近似值,要使得 的值最小, 应选取这 次测量结果的( )A、中位数 B、众数 C、平均数 D、最小值二、填空题
-
7. 在“大学习、大调研、大攻坚”九个汉字中,随机抽取一个汉字,抽到“大”字的概率为 .8. 若关于 的方程 的一根为1,则方程的另一个根为 .9. 在平面直角坐标系中,菱形 的对角线交于原点 ,点 的坐标为 ,点 的坐标为 ,则点 的坐标为 .10. 如图,两个大小一样的传送轮连接着一条传送带,两个传动轮中心的距离是 ,求这条传送带的长米.
 11. 如图,正方形 的一个顶点与原点 重合, 与 轴的正半轴的夹角为15°,点 在抛物线 的图象上,则 的长为 .
11. 如图,正方形 的一个顶点与原点 重合, 与 轴的正半轴的夹角为15°,点 在抛物线 的图象上,则 的长为 .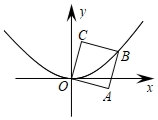 12. 已知在 中, , ,若该三角形的一中线长为 ,则 的长为 .
12. 已知在 中, , ,若该三角形的一中线长为 ,则 的长为 .三、解答题
-
13.(1)、解方程: ;(2)、如图, 中, , ,求 度数.
 14. 若关于 的方程 有两个不相等的实数根,求 的取值范围.15. 一个二次函数的图象经过A(0,0),B(1,9),C(-1,-1),求这个二次函数的解析式.16. “赣江”是长江主要支流之一,江西省最大的河流.其东源出自石城县武夷山,称“绵水”,流经瑞金,在会昌县与“湘水”(江西)汇合,称“贡水”;其西源出自崇义县聂都山,称“章水”.“章水"与“贡水”在赣州市八镜台汇合,是为“赣江”.
14. 若关于 的方程 有两个不相等的实数根,求 的取值范围.15. 一个二次函数的图象经过A(0,0),B(1,9),C(-1,-1),求这个二次函数的解析式.16. “赣江”是长江主要支流之一,江西省最大的河流.其东源出自石城县武夷山,称“绵水”,流经瑞金,在会昌县与“湘水”(江西)汇合,称“贡水”;其西源出自崇义县聂都山,称“章水”.“章水"与“贡水”在赣州市八镜台汇合,是为“赣江”.小丽和小杰一起玩游戏:将“章水”、“贡水”、“绵水”、“湘水”分别写在四张完全相同的卡片正面,把四张卡片背面朝上,洗匀后放在桌面上.小丽从中随机抽取一张卡片,小杰再从剩余的卡片中随机抽取一张卡片.
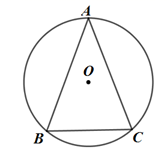
 (1)、“赣江被抽中”是事件,“章水被抽中”是事件(填“不可能”或“必然”或“随机”);(2)、试用画树状图或列表的方法表示所有可能的结果,并求“两人抽取的河流能汇合”的概率.17. 如图, 、 、 均为 上的点,且 ,请你用无刻度的直尺按下列要求作图.
(1)、“赣江被抽中”是事件,“章水被抽中”是事件(填“不可能”或“必然”或“随机”);(2)、试用画树状图或列表的方法表示所有可能的结果,并求“两人抽取的河流能汇合”的概率.17. 如图, 、 、 均为 上的点,且 ,请你用无刻度的直尺按下列要求作图. (1)、在图1中,在圆上取点 ,使 ;(2)、在图2中,作出 的一个余角.18. 某数学兴趣小组在探究函数 的图象和性质时,经历了以下探究过程:(1)、列表(完成下列表格).
(1)、在图1中,在圆上取点 ,使 ;(2)、在图2中,作出 的一个余角.18. 某数学兴趣小组在探究函数 的图象和性质时,经历了以下探究过程:(1)、列表(完成下列表格).…
-3
-2
-1
0
1
2
3
…
…
6
3
2
3
3
6
…
(2)、描点并在图中画出函数的大致图象; (3)、根据函数图象,完成以下问题:
(3)、根据函数图象,完成以下问题:①当函数 的图象向下平移个单位时,图象与 轴有三个公共点;
②结合图象探究发现,当 满足时,方程 有四个解.
19. 如图, 中, . 绕点 逆时针旋转,旋转角为 ,点 为点 的对应点. (1)、请用尺规作图法画出旋转后的 ;(2)、若 , , .求 的长.20. 返校复学之际,育才学校为每个班级准备了免洗抑菌洗手液.去市场购买时发现当购买量不超过100瓶时,免洗抑菌洗手液的单价为8元;超过100瓶时,每增加10瓶,每瓶单价就降低0.2元,但最低价格不能低于每瓶5元,设学校共买了 瓶免洗抑菌洗手液.(1)、当 时,每瓶洗手液的价格是元;当 时,每瓶洗手液的价格是元;当 时,每瓶洗衣手液的价格为元(用含 的式子表示);(2)、若学校一次性购买洗手液共花费1250元,问一共购买了多少瓶洗手液?21. 如图,半 的直径 , 为半圆一动点(不与 , 重合), 的延长线与直线 相交于点 ,且 .
(1)、请用尺规作图法画出旋转后的 ;(2)、若 , , .求 的长.20. 返校复学之际,育才学校为每个班级准备了免洗抑菌洗手液.去市场购买时发现当购买量不超过100瓶时,免洗抑菌洗手液的单价为8元;超过100瓶时,每增加10瓶,每瓶单价就降低0.2元,但最低价格不能低于每瓶5元,设学校共买了 瓶免洗抑菌洗手液.(1)、当 时,每瓶洗手液的价格是元;当 时,每瓶洗手液的价格是元;当 时,每瓶洗衣手液的价格为元(用含 的式子表示);(2)、若学校一次性购买洗手液共花费1250元,问一共购买了多少瓶洗手液?21. 如图,半 的直径 , 为半圆一动点(不与 , 重合), 的延长线与直线 相交于点 ,且 .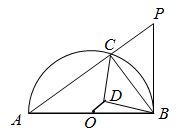 (1)、求证: 为半 的切线;(2)、若 是 的平分线,且 于 ,连接 .
(1)、求证: 为半 的切线;(2)、若 是 的平分线,且 于 ,连接 .①请判断线段 与 有什么位置关系,并说明理由;
②当 时,则 的长为 ▲ .
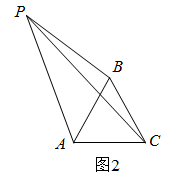
22. 已知二次函数y=ax2﹣2ax .(1)、二次函数图象的对称轴是直线x=;(2)、当0≤x≤3时,y的最大值与最小值的差为4,求该二次函数的表达式;(3)、若a<0,对于二次函数图象上的两点P(x1 , y1),Q(x2 , y2),当t≤x1≤t+1,x2≥3时,均满足y1≥y2 , 请结合函数图象,直接写出t的取值范围.23. (问题提出)如图1,在等边三角形 内部有一点 , , , .求 的度数.(数学思考)当图形中有一组邻边相等时,通过旋转可以将分散的条件集中起来解决问题.

 (1)、(尝试解决)
(1)、(尝试解决)将 绕点 逆时针旋转60°,得到 ,连接 ,则 为等边三角形.
, , ,
为三角形
的度数为 .
(2)、(类比探究)如图2,在等边三角形 外部有一点 ,若 ,求证 .
(3)、(联想拓展)如图3,在 中, , .点 在直线 上方且 , ,求 的长.