江西省赣州市寻乌县2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-04-01 类型：期末考试

进入出卷网下载

一、单选题

1. 已知 $\sqrt{3}$ 是方程x²﹣3 $\sqrt{3}$ x+c＝0的一个根，则c的值是（）

A、﹣6 B、6 C、 $\sqrt{3}$ D、2 $\sqrt{3}$

查看试题解析
2. 抛物线y=（x+2）²﹣2的顶点坐标是（）

A、（2，﹣2） B、（2，2） C、（﹣2，2） D、（﹣2，﹣2）

查看试题解析
3. 如图，AB为⊙O的直径，点C为⊙O上的一点，过点C作⊙O的切线，交直径AB的延长线于点D；若∠A＝23°，则∠D的度数是（）

A、23° B、44° C、46° D、57°

查看试题解析
4. 如图，将△ABC绕点A按逆时针方向旋转100°，得到△AB₁C₁ ，若点B₁在线段BC的延长线上，则∠BB₁C₁的大小为（）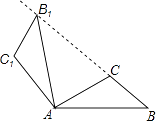

A、70° B、80° C、84° D、86°

查看试题解析
5. 如图，一飞镖游戏板由大小相等的小正方形格子构成，向游戏板随机投掷一枚飞镖，击中黑色区域的概率是（）

A、 $\frac{4}{9}$ B、 $\frac{5}{9}$ C、 $\frac{1}{5}$ D、 $\frac{1}{4}$

查看试题解析
6. 如图，已知抛物线y＝ax²+bx+c与x轴交于A ， B两点，顶点C的纵坐标为﹣2，现将抛物线向右平移2个单位，得到抛物线y＝a₁x²+b₁x+c₁ ，则下列结论：①b＞0；②a﹣b+c＜0；③阴影部分的面积为4；④若c＝﹣1，则b²＝4a ．其中正确的个数为（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

7. 已知二次函数 $y = x^{2} - m x + 3$ 在 $x = 0$ 和 $x = 2$ 时的函数值相等，那么 $m$ 的值是.

查看试题解析
8. 已知 $α, β$ 方程 $x^{2} + 2 x - 5 = 0$ 的两根，那么 $α^{2} + 3 α + β$ 的值是．

查看试题解析
9. 在一个不透明的口袋中有颜色不同的红、白两种小球，其中红球3只，白球n只，若从袋中任取一个球，摸出白球的概率为 $\frac{3}{4}$ ，则n= ．

查看试题解析
10. 二次函数y＝x²－4x＋3的图象交x轴于A、B两点，交y 轴于点C，则△ABC的面积为

查看试题解析
11. 如图，四边形ABCD内接于⊙O ， ∠C=130°，则∠BOD的度数是．

查看试题解析
12. 如图，正方形 $A B C D$ 的边长为8，M是 $A B$ 的中点，一动点P从点 $B - C - D$ 运动，连接 $P M$ ，以点P为圆心， $P M$ 的长为半径作 $⊙ P$ ，当 $⊙ P$ 与正方形 $A B C D$ 的边相切时， $B P$ 的长为．

查看试题解析

三、解答题

13.

(1)、解方程： $x (x - 4) = - 2 (x - 4)$ ；

(2)、已知：如图， $⊙ O$ 的直径 $A B$ 与弦 $C D$ （不是直径）交于点F ，若FB=2，CF=FD=4，设 $⊙ O$ 的半径为r ，求 $A C$ 的长．

查看试题解析
14. 已知关于x的一元二次方程 $x^{2} - 2 k x + k^{2} + k + 1 = 0$ 有两个实数根．

(1)、试求k的取值范围；

(2)、若此方程的两个实数根 $x_{1} 、 x_{2}$ ，是否存在实数k ，满足 $\frac{1}{x_{1}} + \frac{1}{x_{2}} = - 2$ ，若存在，求出k的值；若不存在，说明理由．

查看试题解析
15. 在如图所示的正方形网格中， $△ A B C$ 的顶点均在格点上，请在所给直角坐标系中按要求画图和解答下列问题：

(1)、作出 $△ A B C$ 关于坐标原点O成中心对称的 $△ A_{1} B_{1} C_{1}$ ，画出 $△ A_{1} B_{1} C_{1}$ ，写出 $C_{1}$ 坐标；

(2)、将 $△ A B C$ 绕点O逆时针旋转 $90 °$ 得到 $△ A_{2} B_{2} C_{2}$ ，写出 $C_{2}$ 的坐标．

查看试题解析
16. 已知，点A ， B ， C在 $⊙ O$ 上， $∠ C = 34 °$ ，请仅用无刻度的直尺作图（保留作图痕迹，不写作法）．

(1)、在如图①中画出一个含 $56 °$ 角的直角三角形；

(2)、点D在弦 $A B$ 上，在如图②中画出一个含 $56 °$ 的直角三角形．

查看试题解析
17. 将两块大小相同的含 $30 °$ 角的直角三角板（ $∠ B A C = ∠ B^{'} A^{'} C = 30 °$ ）按图①的方式放置，固定三角板 $A^{'} B^{'} C$ ，然后将三角板 $A B C$ 绕直角顶点C顺时针方向旋转（旋转角小于 $90 °$ ）至图②所示的位置， $A B$ 与 $A^{'} C$ 交于点E ， $A C$ 与 $A^{'} B^{'}$ 交于点F ， $A B$ 与 $A^{'} B^{'}$ 交于点O ．

(1)、求证： $△ B C E ≌ △ B^{'} C F$ ；

(2)、当旋转角等于 $30 °$ 时， $A B$ 与 $A^{'} B^{'}$ 垂直吗？请说明理由．

查看试题解析
18. 在湖州创建国家卫生文明城市的过程中，张辉和夏明积极参加志愿者活动，当时有下列四个志愿者工作岗位供他们选择：
①清理类岗位：清理花坛卫生死角；清理楼道杂物（分别用 $A_{1} ， A_{2}$ 表示）。
②宣传类岗位：垃圾分类知识宣传；交通安全知识宣传（分别用 $B_{1} ， B_{2}$ 表示）。

(1)、张辉同学从四个岗位中随机选取一个报名，恰好选择清理类岗位概率为是；

(2)、若张辉和夏明各随机从四个岗位中选一个报名，请你利用树状图或列表法求出他们恰好都选择同一个岗位的概率．

查看试题解析
19. 已知如图，在△ABC中，AB=BC=4，∠ABC=90°，M是AC的中点，点N在AB上（不同于A、B），将△ANM绕点M逆时针旋转90°得△A₁PM

(1)、画出△A₁PM

(2)、设AN=x，四边形NMCP的面积为y，直接写出y关于x的函数关系式，并求y的最大或最小值．

查看试题解析
20. 我市某楼盘准备以每平方米8000元的均价对外销售，由于国务院有关房地产的新政策出台后，购房者持币观望，房地产开发商为了加快资金周转，对价格经过两次下调后，决定以每平方米6480元的均价开盘销售

(1)、求平均每次下调的百分率．

(2)、某人准备以开盘价均价购买一套100平方米的住房，开发商给予以下两种优惠方案以供选择：
①打9.8折销售；

②不打折，一次性送装修费每平方米80元．

试问哪种方案更优惠？

查看试题解析
21. 已知二次函数 $y = a x^{2} + b x + \frac{3}{2}$ 的图象的对称轴是直线 $x = 1$ ，它与x轴交于A、B两点，与y轴交于点C ，点A的坐标是 $(- 1 ， 0)$ ．

(1)、请在平面直角坐标系内画出示意图，并根据图象直接写出 $y > 0$ 时x的取值范围；

(2)、求此图象所对应的函数关系式；

(3)、若点P是此二次函数图象上位于x轴上方的一个动点，求 $△ A B P$ 面积的最大值．

查看试题解析
22. 如图，AB是⊙O的直径，∠BAC＝90°，四边形EBOC是平行四边形，EB交⊙O于点D，连接CD并延长交AB的延长线于点F．

(1)、求证：CF是⊙O的切线；

(2)、若∠F＝30°，EB＝8，求图中阴影部分的面积．（结果保留根号和π）

查看试题解析
23. 如图，已知抛物线 $C_{1}$ 与x轴交于 $A (4 ， 0) ， B (- 1 ， 0)$ 两点，与y轴交于点 $C (0 ， 2)$ ．将抛物线 $C_{1}$ 向右平移 $m (m > 0)$ 个单位得到抛物线 $C_{2} ， C_{2}$ 与x轴交于D ， E两点（点D在点E的左侧），与抛物线 $C_{1}$ 在第一象限交于点M ．

(1)、求抛物线 $C_{1}$ 的解析式，并求出其对称轴；

(2)、①当 $m = 1$ 时，直接写出抛物线 $C_{2}$ 的解析式；
②直接写出用含m的代数式表示点M的坐标；

(3)、连接 $D M ， A M$ ．在抛物线 $C_{1}$ 平移的过程中，是否存在 $△ A D M$ 是等边三角形的情况？若存在，请求出此时m的值；若不存在，请说明理由．

查看试题解析