江西省赣州市定南县2020-2021学年九年级上学期数学期末试卷

试卷更新日期：2021-04-01 类型：期末考试

进入出卷网下载

一、单选题

1. 关于 $x$ 的方程 $(a - 1) x^{2} - 3 x + 2 = 0$ 是一元二次方程，则（）

A、 $a > 0$ B、 $a \neq 0$ C、 $a \neq 1$ D、 $a = 1$

查看试题解析
2. 下列图形既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列函数：① $y = x - 2$ ，② $y = \frac{3}{x}$ ，③ $y = x^{2}$ ，④ $y = x^{2} + 3 x + 4$ ， $y$ 是 $x$ 的反比例函数的个数有（）．

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 不透明袋子中装有若干个红球和6个蓝球，这些球除了颜色外，没有其他差别，从袋子中随机摸出一个球，摸出蓝球的概率是0.6，贝袋子中有红球（）

A、2个 B、4个 C、6个 D、8个

查看试题解析
5. 如图，在△ABC中，∠ACB=90°，∠A=40°，以C为圆心，CB为半径的圆交AB于点D，连接CD，则∠ACD=（）

A、10° B、15° C、20° D、25°

查看试题解析
6. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图，给出下列四个结论：① $a c - b^{2} < 0$ ；② $3 b + 2 c < 0$ ；③ $m (a m + b) + b \leq a$ ；④ ${(a + c)}^{2} < b^{2}$ ；其中正确结论的个数有（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

7. 设 $x_{1}$ ， $x_{2}$ 是方程 $x^{2} + 5 x + 2 = 0$ 的两个根，则 $x_{1} \cdot x_{2} =$ ．

查看试题解析
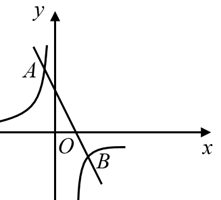
8. 若反比例函数 $y = \frac{2 - k}{x}$ 的图象在第一、三象限，则k的取值范围是

查看试题解析
9. 设 $A (- 2 ， y_{1})$ ， $B (1 ， y_{2})$ ， $C (2 ， y_{3})$ 是抛物线 $y = - {(x + 1)}^{2} + k$ 上的三点，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系为．

查看试题解析
10. 技术变革带来产品质量的提升.某企业技术变革后，抽检某一产品2020件，欣喜发现产品合格的频率已达到0.9911，依此我们可以估计该产品合格的概率为.（结果要求保留两位小数）

查看试题解析
11. 如图，平面直角坐标系中，点B在第一象限，点A在x轴的正半轴上，∠AOB＝∠B＝30°，OA＝2，将△AOB绕点O逆时针旋转90°，点B的对应点B'的坐标是

查看试题解析
12. 如图， $A B$ 为半圆的直径， $A B = 10$ ，点 $O$ 到弦 $A C$ 的距离为4，点 $P$ 从 $B$ 出发沿 $B A$ 方向向点 $A$ 以每秒1个单位长度的速度运动，连接 $C P$ ，经过秒后， $Δ A P C$ 为等腰三角形．

查看试题解析

三、解答题

13.

(1)、解方程： $x^{2} - 4 x - 5 = 0$

(2)、已知点 $P (2 x + y, 1)$ 与点 $Q (- 7, x - y)$ 关于原点对称，求 $x$ ， $y$ 的值．

查看试题解析
14. 已知二次函数的图象的顶点为 $(1, - 3)$ ，且过点 $P (2, 0)$ ，求这个二次函数的解析式.

查看试题解析
15. 一个不透明的口袋里装有分别标有汉字“优”、“秀”、“学”、“生”的四个小球，除汉字不同之外，小球没有任何区别，每次摸球前先搅拌均匀．

(1)、若从中任取一个球，球上的汉字刚好是“优”的的概率是；

(2)、从中任取一球，不放回，再从中任取一球，请用树状图或列表的方法，求取出两个球上的汉字能组成“优秀”或“学生”的概率．

查看试题解析
16. 如图，请用无刻度的直尺按下列要求画图（不写作法，保留作图痕迹）．

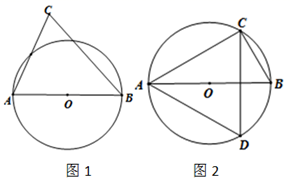(1)、如图1，已知 $△ A B C$ ， $A B = B C$ ，以 $A B$ 为直径的 $⊙ O$ 相交，请作出 $∠ A B C$ 的平分线 $B P$ ．

(2)、如图2，已知 $△ A C D$ 中， $A D = C D$ ，以 $A B$ 为直径的 $⊙ O$ 经过 $A$ ， $C$ ， $D$ 三点，请作出 $∠ A B C$ 的平分线 $B Q$ ．

查看试题解析
17. 在平面直角坐标系内，点 $O$ 为坐标原点，一次函数 $y = k x + b$ 的图象与反比例函数 $y = \frac{m}{x}$ 的图象交于 $A$ ， $B$ 两点，若 $A (4, 1)$ ，点 $B$ 的横坐标为 $- 2$ ，求反比例函数及一次函数的解析式．

查看试题解析
18. 如图，平面直角坐标系内，小正方形网格的边长为1个单位长度， $Δ A B C$ 的三个顶点的坐标分别为 $A (- 1 ， 3)$ ， $B (- 4 ， 0)$ ， $C (0 ， 0)$ ，解答下列问题：

(1)、将 $Δ A B C$ 向上平移1个单位长度，再向右平移5个单位长度后得到的 $Δ A_{1} B_{1} C_{1}$ ，画出 $Δ A_{1} B_{1} C_{1}$ ；

(2)、 $Δ A B C$ 绕原点 $O$ 逆时针方向旋转 $90 °$ 得到 $Δ A_{2} B_{2} O$ ，画出 $Δ A_{2} B_{2} O$ ；

(3)、如果利用 $Δ A_{2} B_{2} O$ 旋转可以得到 $Δ A_{1} B_{1} C_{1}$ ，请直接写出旋转中心 $P$ 的坐标.

查看试题解析
19. 如图，在△ABC中，AB=AC，∠BAC=120°，点D在BC边上， $⊙$ D经过点A和点B且与BC边相交于点E.

(1)、求证：AC是 $⊙$ D的切线.

(2)、若CE= $2 \sqrt{3}$ ，求 $⊙$ D的半径.

查看试题解析
20. 某水果批发商场经销一种高档水果，如果每千克盈利10元，每天可售出500千克．经市场调查发现，在进货价不变的情况下，若每千克涨价1元，日销售量将减少20千克．

(1)、现该商场要保证每天盈利6 000元，同时又要顾客得到实惠，那么每千克应涨价多少元？

(2)、若该商场单纯从经济角度看，每千克这种水果涨价多少元，能使商场获利最多？

查看试题解析
21. 如图，已知 $A B$ 是 $⊙ O$ 的直径， $C$ ， $D$ 是 $⊙ O$ 上的点， $O C / / B D$ ，交 $A D$ 于点 $E$ ，连结 $B C$ ．

(1)、求证： $A E = D E$ ；

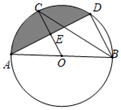(2)、若 $A B = 8$ ， $∠ C B D = 30 °$ ，求图中阴影部分的面积．

查看试题解析
22. 如图，在平面直角坐标系中，一次函数 $y = k x + b$ 与反比例函数 $y = - \frac{6}{x}$ 的图象交于 $A (- 1 ， m)$ ， $B (n ， - 3)$ 两点，一次函数 $y = k x + b$ 的图象与 $y$ 轴交于点 $C$ ．

(1)、求一次函数的解析式；

(2)、根据函数的图象，直接写出不等式 $k x + b \geq - \frac{6}{x}$ 的解集；

(3)、点 $P$ 是 $x$ 轴上一点，且 $Δ B O P$ 的面积等于 $Δ B O A$ 面积，求点 $P$ 的坐标．

查看试题解析
23. 如图，在平面直角坐标系中， $Δ O A C$ 绕点 $O$ 顺时针旋转 $90 °$ 得到 $Δ O N B$ ， $O B = O C = 3$ ，抛物线 $y = - x^{2} + b x + c$ 经过 $A$ ， $B$ ， $C$ 三点．

(1)、求抛物线的解析式；

(2)、如图①点 $D$ 是抛物线的顶点，试判定 $Δ B N D$ 的形状，并加以证明；

(3)、如图②在第一象限的抛物线上，是否存在点 $M$ ，使 $S_{Δ M B N} = 2 S_{Δ A O C}$ ？若存在，请求点 $M$ 的坐标；若不存在，请说明理由．

查看试题解析