江西省抚州市2020-2021学年九年级上学期数学期末试卷
试卷更新日期:2021-04-01 类型:期末考试
一、单选题
-
1. 下列线段中,能成比例的是( )A、3cm、6cm、8cm、9cm B、3cm、5cm、6cm、9cm C、3cm、6cm、7cm、9cm D、3cm、6cm、9cm、18cm2. 如图是某体育馆内的颁奖台,其主视图是( )
 A、
A、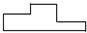 B、
B、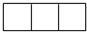 C、
C、 D、
D、 3. 已知反比例函数y= ,下列结论中错误的是( )A、图象经过点(﹣1,﹣1) B、当x<0时,y随着x的增大而增大 C、当x>1时,0<y<1 D、图象在第一、三象限4. 将抛物线 先向左平移1个单位长度,再向上平移2个单位长度,所得抛物线的解析式是( )A、 B、 C、 D、5. 一元二次方程x2﹣3x+1=0的两个根为x1 , x2 , 则x12+3x2+x1x2+1的值为( )A、10 B、9 C、8 D、76. 已知二次函数 的图象如图所示,有下列4个结论:
3. 已知反比例函数y= ,下列结论中错误的是( )A、图象经过点(﹣1,﹣1) B、当x<0时,y随着x的增大而增大 C、当x>1时,0<y<1 D、图象在第一、三象限4. 将抛物线 先向左平移1个单位长度,再向上平移2个单位长度,所得抛物线的解析式是( )A、 B、 C、 D、5. 一元二次方程x2﹣3x+1=0的两个根为x1 , x2 , 则x12+3x2+x1x2+1的值为( )A、10 B、9 C、8 D、76. 已知二次函数 的图象如图所示,有下列4个结论: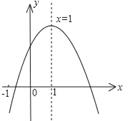
① ;② ;③ ;④ ;⑤2c<3b
其中正确的结论有( )
A、2个 B、3个 C、4个 D、5个二、填空题
-
7. 抛物线y=(x+2)2+1的顶点坐标为 .8. 如图,体育兴趣小组选一名身高1.6m的同学直立于旗杆影子的顶端处,其他人分为两部分,一部分同学测得该同学的影长为1.2m,另一部分同学测得同一时刻旗杆影长为9m,那么旗杆的高度是m.
 9. 若 ,那么△ABC的形状是 .10. 如图,在边长为1的小正方形网格中,点A , B , C , D都在这些小正方形的顶点上,AB , CD相交于点O , 则cos∠BOD= .
9. 若 ,那么△ABC的形状是 .10. 如图,在边长为1的小正方形网格中,点A , B , C , D都在这些小正方形的顶点上,AB , CD相交于点O , 则cos∠BOD= .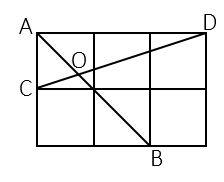 11. 如图,在▱ABCD中,对角线AC , BD相交于点O , 在DC的延长线上取一点E , 使CE= CD , 连接OE交BC于点F , 若BC=4,则CF= .
11. 如图,在▱ABCD中,对角线AC , BD相交于点O , 在DC的延长线上取一点E , 使CE= CD , 连接OE交BC于点F , 若BC=4,则CF= .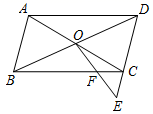 12. 如图, , , AB=6,CD=4,BD=14.点P在BD上移动,当以P , C , D为顶点的三角形与△ABP相似时,则PB的长为 .
12. 如图, , , AB=6,CD=4,BD=14.点P在BD上移动,当以P , C , D为顶点的三角形与△ABP相似时,则PB的长为 .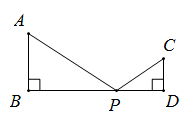
三、解答题
-
13.(1)、解方程: ;(2)、计算: .14. 已知 是方程 的一个根,求方程的另一个根及c的值.15. 如图,是由两个等边三角形和一个正方形拼在-起的图形,请仅用无刻度的直尺按要求画图,
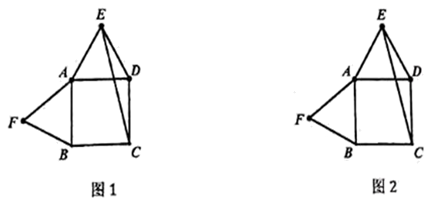 (1)、在图①中画一个 的角,使点 或点 是这个角的顶点,且以 为这个角的一边:(2)、在图②画一条直线 ,使得 .16. 江西两所医院分别有一男一女共4名医护人员支援湖北随州抗击疫情.(1)、若从甲、乙两医院支援的医护人员中分别随机选1名,则所选的2名医护人员性别相同的概率是 .(2)、若从支援的4名医护人员中随机选2名,用列表或画树状图的方法求出这2名医护人员来自同一所医院的概率.17. 如图,把一张矩形纸片沿对角线折叠.
(1)、在图①中画一个 的角,使点 或点 是这个角的顶点,且以 为这个角的一边:(2)、在图②画一条直线 ,使得 .16. 江西两所医院分别有一男一女共4名医护人员支援湖北随州抗击疫情.(1)、若从甲、乙两医院支援的医护人员中分别随机选1名,则所选的2名医护人员性别相同的概率是 .(2)、若从支援的4名医护人员中随机选2名,用列表或画树状图的方法求出这2名医护人员来自同一所医院的概率.17. 如图,把一张矩形纸片沿对角线折叠.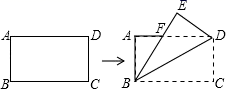 (1)、重合部分是什么图形?请说明理由.(2)、若AB=4,BC=8,求△BDF的面积.18. 已知:二次函数y=ax2+bx+c(a≠0)中的x和y满足表:
(1)、重合部分是什么图形?请说明理由.(2)、若AB=4,BC=8,求△BDF的面积.18. 已知:二次函数y=ax2+bx+c(a≠0)中的x和y满足表:x
…
﹣1
0
1
2
3
…
y
…
3
0
﹣1
0
m
…
(1)、观察表可求得m的值为;(2)、请求出这个二次函数的表达式.19. 阳光市场某个体商户购进某种电子产品,每个进价50元.调查发现,当售价为80元时,平均一周可卖出160个,而当每售价每降低2元时,平均一周可多卖出20个.若设每个电子产品降价x元,(1)、根据题意,填表:进价(元)
售价(元)
每件利润(元)
销量(个)
总利润(元)
降价前
50
80
30
160
降价后
50
(2)、若商户计划每周盈利5200元,且尽量减少库存,则每个电子产品应降价多少元?20. 为倡导“绿色出行,低碳生活”的号召,今年春天,安庆市的街头出现了一道道绿色的风景线--“共享单车”. 图(1)所示的是一辆共享单车的实物图. 图(2)是这辆共享单车的部分几何示意图,其中车架档AC长为40cm,座杆CE的长为18cm. 点A、C、E在同一条直线上,且∠CAB=60°,∠ACB=75°
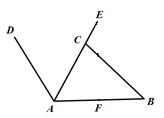 (1)、求车座点E到车架档AB的距离;(2)、求车架档AB的长.21. 已知正比例函数y1=ax的图象与反比例函数y2= 的图象交于A , B两点,且A点的横坐标为﹣1.
(1)、求车座点E到车架档AB的距离;(2)、求车架档AB的长.21. 已知正比例函数y1=ax的图象与反比例函数y2= 的图象交于A , B两点,且A点的横坐标为﹣1.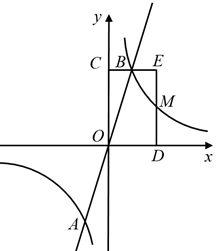 (1)、试确定上述正比例函数和反比例函数的表达式.(2)、根据图象回答,当x取何值时,反比例函数的值大于正比例函数的值.(3)、点M(m , n)是反比例函数图象上一动点,其中0<n<3,过点M作MD∥y轴交x轴于点D , 过点B作BC∥x轴交y轴于点C , 交直线MD于点E , 当四边形OMEB面积为3时,请判断DM与EM大小关系并给予证明.22. 如图
(1)、试确定上述正比例函数和反比例函数的表达式.(2)、根据图象回答,当x取何值时,反比例函数的值大于正比例函数的值.(3)、点M(m , n)是反比例函数图象上一动点,其中0<n<3,过点M作MD∥y轴交x轴于点D , 过点B作BC∥x轴交y轴于点C , 交直线MD于点E , 当四边形OMEB面积为3时,请判断DM与EM大小关系并给予证明.22. 如图
如图1,把两个相似比为 的矩形ABCD与矩形CEFG拼成如图所示的图案.
(1)、(一)问题发现:请探究AC与CF的位置关系并证明.
(2)、求 的值.(3)、(二)拓展应用:如图2,在四边形ABCF中,已知∠ABC=90°,AB=3,BC=4,CF=10,AF=5 .
求tan∠AFC;
(4)、连接BF , 求BF的长.23. 定义:在平面直角坐标系中,抛物线y=a +bx+c(a≠0)与直线y=m交于点A、C(点C在点A右边)将抛物线y=a +bx+c沿直线y=m翻折,翻折前后两抛物线的顶点分别为点B、D.我们将两抛物线之间形成的封闭图形称为惊喜线,四边形ABCD称为惊喜四边形,对角线BD与AC之比称为惊喜度(Degreeofsurprise),记作|D|= .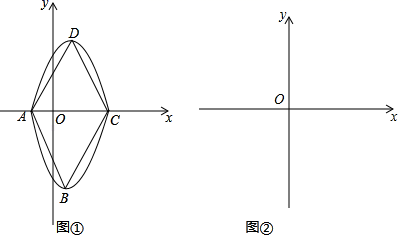 (1)、图①是抛物线y= ﹣2x﹣3沿直线y=0翻折后得到惊喜线.则点A坐标 , 点B坐标 , 惊喜四边形ABCD属于所学过的哪种特殊平行四边形 , |D|为 .(2)、如果抛物线y=m ﹣6m(m>0)沿直线y=m翻折后所得惊喜线的惊喜度为1,求m的值.(3)、如果抛物线y= ﹣6m沿直线y=m翻折后所得的惊喜线在m﹣1≤x≤m+3时,其最高点的纵坐标为16,求m的值并直接写出惊喜度|D|.
(1)、图①是抛物线y= ﹣2x﹣3沿直线y=0翻折后得到惊喜线.则点A坐标 , 点B坐标 , 惊喜四边形ABCD属于所学过的哪种特殊平行四边形 , |D|为 .(2)、如果抛物线y=m ﹣6m(m>0)沿直线y=m翻折后所得惊喜线的惊喜度为1,求m的值.(3)、如果抛物线y= ﹣6m沿直线y=m翻折后所得的惊喜线在m﹣1≤x≤m+3时,其最高点的纵坐标为16,求m的值并直接写出惊喜度|D|.