云南省玉溪市峨山县2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-04-01 类型：期末考试

进入出卷网下载

一、填空题

1. 蜜蜂建造的蜂巢既坚固又省料，其厚度约为0.000073米，将0.000073用科学记数法表示为．

查看试题解析
2. 分解因式：x²+x＝．

查看试题解析
3. 一个 $n$ 边形的内角和等于外角和的2倍，则其边数 $n$ 为．

查看试题解析
4. 已知等腰三角形的一个内角是80°，则它的底角是°．

查看试题解析
5. 如果 $x^{2} - 10 x + m$ 是一个完全平方式，那么m的值是．

查看试题解析
6. 如图，在△ABC中，∠C=90°，直线DE是AB的垂直平分线，AD恰好平分∠BAC．若DE=2，则BC的长为．

查看试题解析

二、单选题

7. 低碳环保理念深入人心，共享单车已成为出行新方式．下列共享单车图标，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
8. 在△ABC中，AB=3，AC=5，第三边BC的取值范围是（）

A、10＜BC＜1 B、4＜BC＜12 C、3＜BC＜8 D、2＜BC＜8

查看试题解析
9. 下列计算正确的是（）

A、 ${(m^{3})}^{2} = m^{5}$ B、 $m^{3} \cdot m^{7} = m^{10}$ C、 ${(- 3 m^{2})}^{3} = - 9 m^{6}$ D、 $m^{6} \div m^{3} = m^{2}$

查看试题解析
10. 若分式 $\frac{x^{2} - 1}{x + 1}$ 的值为0，则x的值为（）

A、0 B、1 C、﹣1 D、±1

查看试题解析
11. 如图，D在AB上，E在AC上，且∠B=∠C，则在下列条件中，无法判定△ABE≌△ACD的是（）

A、AD=AE B、AB=AC C、BE=CD D、∠AEB=∠ADC

查看试题解析
12. 若 $a = b + 3$ ，则 $a^{2} - 2 a b + b^{2}$ 的值为（）

A、3 B、6 C、9 D、12

查看试题解析
13. 某工厂计划生产300个零件，由于采用新技术，实际每天生产零件的数量是原计划的2倍，因此提前5天完成任务.设原计划每天生产零件x个，根据题意，所列方程正确的是（）

A、 $\frac{300}{x}$ ﹣ $\frac{300}{x + 2}$ ＝5 B、 $\frac{300}{2 x}$ ﹣ $\frac{300}{x}$ ＝5 C、 $\frac{300}{x}$ ﹣ $\frac{300}{2 x}$ ＝5 D、 $\frac{300}{x + 2}$ ﹣ $\frac{300}{x}$ ＝5

查看试题解析
14. 如图，在△ABC中，AB=AC，AB＞BC，点D在BC边上，BD= $\frac{1}{2}$ DC，∠BED=∠CFD=∠BAC，若S_△ABC=30，则阴影部分的面积为（）

A、5 B、10 C、15 D、20

查看试题解析

三、解答题

15. 计算： ${(- 1)}^{2020} - {(π - 1)}^{0} + | - 4 | - {(\frac{1}{3})}^{- 2}$

查看试题解析
16. 化简： ${(2 x + 3)}^{2} - (2 x - 1) (2 x + 1)$

查看试题解析
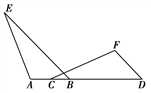
17. 解方程： $\frac{x}{2 x - 3} + \frac{5}{3 - 2 x} = 4$

查看试题解析
18. 如图，点A，C，B，D在同一条直线上，BE∥DF，∠A=∠F，AB=FD，求证：AE=FC.

查看试题解析
19. 先化简代数式 $(1 - \frac{3}{a + 2}) \div \frac{a^{2} - 2 a + 1}{a^{2} - 4}$ ，再从－2，2，0三个数中选一个恰当的数作为a的值代入求值.

查看试题解析
20. 如图，已知A（1，2），B（4，1），C（3，－2）．

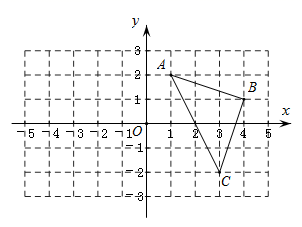(1)、画出△ABC关于y轴对称的图形△A₁B₁C₁；

(2)、写出A₁、B₁、C₁三点的坐标；

(3)、P为x轴上一点，请在图中画出使PA＋PB最小时的点P，并直接写出此时点P的坐标．（保留作图痕迹）

查看试题解析
21. 冠状病毒病感染的疫情牵动着全国人民的心，病毒无情，人间有爱．疫情爆发初期，某中学学生会号召同学们用自己的压岁钱捐献爱心．已知七年级捐款总额为16000元，八年级捐款总额为14000元，七年级捐款人数比八年级多20人，而且两个年级人均捐款额相等，请问七、八年级捐款的人数分别为多少人？

查看试题解析
22. 如图，在△ABC中，AB＝AC，D为BC边上一点，∠B＝30°，∠DAB＝45°.

(1)、求∠DAC的度数；

(2)、求证：DC＝AB.

查看试题解析
23. 如图①，在等边△ABC中，线段AM为BC边上的中线．动点D在直线AM上时，以CD为一边在CD的下方作等边△CDE，连结BE．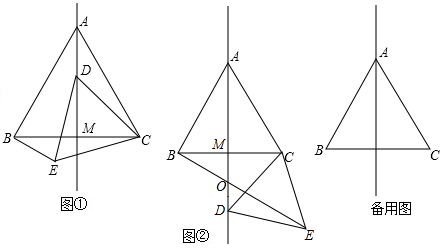

(1)、当点D在线段AM上时（如图①），则ADBE（填“＞”“＜”或“=”），∠CAM= 度；

(2)、当点D在线段AM的延长线上时（如图②），直线BE与直线AM的交点为O，求∠AOB的度数；

(3)、当动点D在线段AM的反向延长线上时，直线BE与直线AM的交点为O，试判断∠AOB的度数是否发生变化？若变化，请求出∠AOB的度数，若不变，请说明理由．

查看试题解析