云南省保山市腾冲市2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-04-01 类型：期末考试

进入出卷网下载

一、填空题

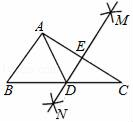
1. 10月30日，钟南山院士表示，从全球视角来看，第二波新冠肺炎疫情已经开始，我们切不可掉以轻心，要做好日常防护．导致新冠肺炎的新冠病毒比细菌小很多，平均直径仅为 $0.00000098 m$ ．这个数用科学记数法表示为 $m$ ．

查看试题解析
2. 已知 $a - b = 14 ， a b = 6$ ，则 $a^{2} + b^{2}$ ＝．

查看试题解析
3. 当 $x$ ＝时，分式 $\frac{x^{2} - 1}{x^{2} + 1}$ 的值为零．

查看试题解析
4. 已知点 $M (- 4 ， y)$ 与点 $N (x ， - 3)$ 关于 $x$ 轴对称，则 ${(x + y)}^{2021}$ 的值为．

查看试题解析
5. 如图，在△ABC中，分别以点A和点C为圆心，大于 $\frac{1}{2}$ AC长为半径画弧，两弧相交于点M、N，作直线MN分别交BC、AC于点D、E，若△ABC的周长为23cm，△ABD的周长为13cm，则AE为cm.

查看试题解析
6. 如图，下列图形是将正三角形按一定规律排列，则第4个图形中所有正三角形的个数有．

查看试题解析

二、单选题

7. 下列图形不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
8. 下列计算正确的是（）

A、 $a^{2} \cdot a = a^{2}$ B、 $a^{6} \div a^{2} = a^{3}$ C、 $a^{2} b - 2 b a^{2} = - a^{2} b$ D、 ${(- \frac{3}{2 a})}^{3} = - \frac{9}{8 a^{3}}$

查看试题解析
9. 若等腰三角形中有一个角等于50°，则这个等腰三角形的顶角的度数为（）

A、50° B、80° C、65°或50° D、50°或80°

查看试题解析
10. 已知三角形的两边长分别为1和4，则第三边长可能是（）

A、3 B、4 C、5 D、6

查看试题解析
11. 一个多边形的内角和是外角和的2倍，这个多边形是（）

A、四边形 B、五边形 C、六边形 D、八边形

查看试题解析
12. 如果 $x^{2} - k x y + 9 y^{2}$ 是一个完全平方式，那么k的值是（）

A、3 B、±6 C、6 D、±3

查看试题解析
13.
如图，在△ABC中，AB=AC，∠BAC=108°，点D在BC上，且BD=AB，连接AD，则∠CAD等于（　　）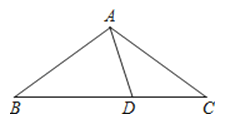

A、30° B、36° C、38° D、45°

查看试题解析
14. 若分式方程 $\frac{x + 2}{x + 3} = \frac{m}{x + 3}$ 无解，则m的值为（）

A、﹣1 B、0 C、1 D、3

查看试题解析

三、解答题

15. 分解因式

(1)、 $3 a x^{2} - 6 a x y + 3 a y^{2}$

(2)、 $x^{2} (x - 2) - 16 (x - 2)$

查看试题解析
16. 计算

(1)、 ${(5 x)}^{2} \cdot x^{7} - {(3 x^{3})}^{3} + 2 {(x^{3})}^{2} + x^{3}$

(2)、 $(x + 2 y) (x - 2 y) - 2 x (x + 3 y) + {(x + y)}^{2}$

查看试题解析
17.

(1)、解分式方程： $\frac{3}{x^{2} - 9} + \frac{x}{x - 3} = 1$

(2)、先化简代数式 $(\frac{a + 1}{a - 1} + \frac{1}{a^{2} - 2 a + 1}) \div \frac{a}{a - 1}$ ，然后选取一个使原式有意义的 $a$ 值代入求值．

查看试题解析
18.
如图：点C是AE的中点，∠A=∠ECD，AB=CD，求证：∠B=∠D．

查看试题解析
19. 在边长为1的小正方形组成的正方形网格中，建立如图所示的平面真角坐标系，已知格点三角形 $A B C$ （三角形的三个顶点都在格点上）

(1)、画出 $Δ A B C$ 关于直线 $x = - 1$ 对称的 $Δ A_{1} B_{1} C_{1}$ ；并写出点 $A_{1}$ 、 $B_{1}$ 、 $C_{1}$ 的坐标．

(2)、在直线 $x = - 1$ 上找一点 $D$ ，使 $B D + C D$ 最小，在图中描出满足条件的 $D$ 点（保留作图痕迹），并写出点 $D$ 的坐标（提示：直线 $x = - 1$ 是过点 $(- 1 ， 0)$ 且垂直于 $x$ 轴的直线）

查看试题解析
20. 如图，点E，F在BC上，BE＝CF，∠A＝∠D，∠B＝∠C，AF与DE交于点O.

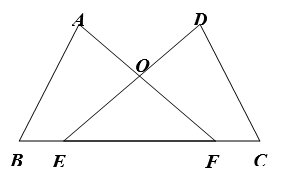(1)、求证：AB＝DC；

(2)、试判断△OEF的形状，并说明理由.

查看试题解析
21. 如图，∠ABC=38°，∠ACB=100°，AD平分∠BAC，AE是BC边上的高，求∠DAE的度数．

查看试题解析
22. 为厉行节能减排，倡导绿色出行，我市推行“共享单车”公益活动．某公司在小区分别投放A、B两种不同款型的共享单车，其中A型车的投放量是B型车的投放量的 $\frac{5}{4}$ 倍，B型车的成本单价比A型车高20元，A型、B型单车投放总成本分别为30000元和26400元，求A型共享单车的成本单价是多少元？

查看试题解析
23. 如图

(1)、某学习小组在探究三角形全等时，发现了下面这种典型的基本图形.如图1，已知：在 $△ A B C$ 中， $∠ B A C = 90^{\circ}$ ， $A B = A C$ ，直线 $l$ 经过点A ， BD⊥直线l ， CE⊥直线l ，垂足分别为点D、E.证明：DE=BD+CE.

(2)、组员小刘想，如果三个角不是直角，那结论是否会成立呢？如图2，将（1）中的条件改为：在 $△ A B C$ 中，AB=AC ， D、A、E三点都在直线l上，并且有 $∠ B D A = ∠ A E C = ∠ B A C = α$ ，其中 $α$ 为任意锐角或钝角．请问结论DE=BD+CE是否成立？如成立，请你给出证明；若不成立，请说明理由.

(3)、数学老师赞赏了他们的探索精神，并鼓励他们运用这个知识来解决问题：如图3，过 $△ A B C$ 的边AB、AC向外作正方形ABDE和正方形ACFG ， AH是BC边上的高，延长HA交EG于点1 ，求证：I是EG的中点.

查看试题解析