山东省潍坊市奎文区2020-2021学年八年级上学期数学期末试卷
试卷更新日期:2021-04-01 类型:期末考试
一、单选题
-
1. 下列疫情防控知识图片是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 根据下列已知条件,不能唯一画出 ABC的是( )A、 , , B、 , , C、 , , D、 , ,3. 若分式 中的a,b都变为原来的2倍,则分式的值( )A、变为原来的4倍 B、变为原来的2倍 C、不变 D、变为原来的4. 一次数学测试,某小组5名同学的成绩统计如下:
2. 根据下列已知条件,不能唯一画出 ABC的是( )A、 , , B、 , , C、 , , D、 , ,3. 若分式 中的a,b都变为原来的2倍,则分式的值( )A、变为原来的4倍 B、变为原来的2倍 C、不变 D、变为原来的4. 一次数学测试,某小组5名同学的成绩统计如下:组员
甲
乙
丙
丁
戊
平均成绩
中位数
得分
81
77
■
80
82
80
■
则被遮盖的两个数据依次是( )
A、80,80 B、81,80 C、80,2 D、81,25. 如图,将▱ABCD沿对角线AC折叠,使点B落在B′处,若∠1=∠2=44°,则∠B为( ) A、66° B、104° C、114° D、124°6. 化简 的结果是( )A、 B、 C、 D、7. 某市为有效解决交通拥堵营造路网微循环,决定对一条长1200米的道路进行拓宽改造.为了减轻施工对城市交通造成的影响,实际施工时,每天改造道路的长度比原计划增加20%,结果提前5天完成任务,求实际每天改造道路的长度和实际施工的天数.一位同学列出方程 ,则方程中未知数x所表示的量是( )A、实际每天改造的道路长度 B、实际施工的天数 C、原计划施工的天数 D、原计划每天改造的道路长度8. 如图,在 中,点D在边BC上,过点D作 , ,分别交AB,AC于E,F两点.则下列命题是假命题的是( )
A、66° B、104° C、114° D、124°6. 化简 的结果是( )A、 B、 C、 D、7. 某市为有效解决交通拥堵营造路网微循环,决定对一条长1200米的道路进行拓宽改造.为了减轻施工对城市交通造成的影响,实际施工时,每天改造道路的长度比原计划增加20%,结果提前5天完成任务,求实际每天改造道路的长度和实际施工的天数.一位同学列出方程 ,则方程中未知数x所表示的量是( )A、实际每天改造的道路长度 B、实际施工的天数 C、原计划施工的天数 D、原计划每天改造的道路长度8. 如图,在 中,点D在边BC上,过点D作 , ,分别交AB,AC于E,F两点.则下列命题是假命题的是( )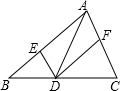 A、四边形 是平行四边形 B、若 ,则四边形 是矩形 C、若 ,则四边形 是菱形 D、若 ,则四边形 是矩形9. 下列选项中,可以用来证明命题“若 ,那么 ”是假命题的反例是( )A、 B、 C、 D、10. 如图,在 中, , ,分别以A、B两点为圆心,大于 的长为半径画弧,两弧相交于点M,N,连接MN,分别与AC,AB交于点D,E.连接BD.则下列结论错误的是( )
A、四边形 是平行四边形 B、若 ,则四边形 是矩形 C、若 ,则四边形 是菱形 D、若 ,则四边形 是矩形9. 下列选项中,可以用来证明命题“若 ,那么 ”是假命题的反例是( )A、 B、 C、 D、10. 如图,在 中, , ,分别以A、B两点为圆心,大于 的长为半径画弧,两弧相交于点M,N,连接MN,分别与AC,AB交于点D,E.连接BD.则下列结论错误的是( ) A、 的周长等于 B、 C、 D、11. 若 ,则下列等式不成立的是( )A、 B、 C、 D、12. 如图,已知正方形ABCD的边长为4,点Р是对角线BD上一动点(不与D,B重合), 于点F, 于点E,连接AP,EF.则下列结论错误的是( )
A、 的周长等于 B、 C、 D、11. 若 ,则下列等式不成立的是( )A、 B、 C、 D、12. 如图,已知正方形ABCD的边长为4,点Р是对角线BD上一动点(不与D,B重合), 于点F, 于点E,连接AP,EF.则下列结论错误的是( ) A、 B、 ,且 C、四边形 的周长是8 D、
A、 B、 ,且 C、四边形 的周长是8 D、二、填空题
-
13. 若分式 的值为0,则x的值为.14. 在一次捐款活动中,某班50名同学人人拿出自己的零花钱,有捐5元、10元、20元的,还有捐50元和100元的.图中的统计图反映了不同捐款数的人数比例,那么该班同学平均每人捐款元.
 15. 如图,在四边形ABCD中,AD=BC , ∠DAB=50°,∠CBA=70°,P、M、N分别是AB , AC、BD的中点,若BC=8,则△PMN的周长是 .
15. 如图,在四边形ABCD中,AD=BC , ∠DAB=50°,∠CBA=70°,P、M、N分别是AB , AC、BD的中点,若BC=8,则△PMN的周长是 .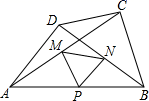 16. 如图,四边形 为菱形,以 为斜边的 的面积为3, ,点E,C在BD的同侧,点P是BD上的一动点,则 的最小值是 .
16. 如图,四边形 为菱形,以 为斜边的 的面积为3, ,点E,C在BD的同侧,点P是BD上的一动点,则 的最小值是 . 17. 若关于 的分式方程 的解为正整数,则满足条件的正数 的值为 .18. 如图,平行四边形 中, 于点E,点F为边AB的中点,连接EF,CF,若 , ,则 .
17. 若关于 的分式方程 的解为正整数,则满足条件的正数 的值为 .18. 如图,平行四边形 中, 于点E,点F为边AB的中点,连接EF,CF,若 , ,则 .
三、解答题
-
19.(1)、化简:(2)、先化简再求值: ,其中 .20. 解方程(1)、(2)、21. 推理填空:
如图, 于D, 于G, ,可得 平分 .
理由如下:∵ 于D, 于G,(已知)
∴ ,( ▲ )
∴ ,( ▲ )
∴ ▲ , ( ▲ )
,( ▲ )
又∵ ,( ▲ )
∴ ▲ , ( ▲ )
∴ 平分 .( ▲ )
 22. 甲、乙两名队员参加射击训练,每次射击的环数均为整数.其成绩分别被制成如下统计图表(乙队员射击训练成绩统计图部分被污染):
22. 甲、乙两名队员参加射击训练,每次射击的环数均为整数.其成绩分别被制成如下统计图表(乙队员射击训练成绩统计图部分被污染):
平均成绩/环
中位数/环
众数/环
方差/环2
甲
7
7
12
乙
7
8
根据以上信息,解决下列问题:
(1)、求出 的值;(2)、直接写出乙队员第7次的射击环数及 的值,并求出 的值;(3)、若要选派其中一名参赛,你认为应选哪名队员?请说明你的理由.23. 如图,在平行四边形ABCD中,对角线AC与BD相交于点O,点E,F分别在BD和DB的延长线上,且 ,连接AE,CF. (1)、求证: ;(2)、连接AF,CE,当BD平分 时,四边形AFCE是什么特殊四边形?请说明理由.24. 列方程解应用题:为厉行节能减排,倡导绿色出行,“共享单车”公益活动登录某市中心城区.某公司拟在甲、乙两个街道社区投放一批“共享单车”,这批“共享单车”包括A,B两种不同款型,请回答下列问题:(1)、该公司早期在甲街区进行了试点投放,投放相同数量的A,B两种款型“共享单车”,投放成本分别是35000元和40000元,其中B型单车的成本单价比A型单车高40元,A,B两种单车的成本单价各是多少?(2)、该公司决定采取如下投放方式:甲街区每1000人投放5a辆“共享单车”,乙街区每1000人投放8a辆“共享单车”,按照这种投放方式,甲街区共投放750辆,乙街区共投放600辆.如果两个街区共有75000人,试求a的值.25. 如图,在 中,对角线AC与BD相交于点O,点M,N分别为OB,OD的中点,连接AM并延长至点E,使 ,连接CE,CN.
(1)、求证: ;(2)、连接AF,CE,当BD平分 时,四边形AFCE是什么特殊四边形?请说明理由.24. 列方程解应用题:为厉行节能减排,倡导绿色出行,“共享单车”公益活动登录某市中心城区.某公司拟在甲、乙两个街道社区投放一批“共享单车”,这批“共享单车”包括A,B两种不同款型,请回答下列问题:(1)、该公司早期在甲街区进行了试点投放,投放相同数量的A,B两种款型“共享单车”,投放成本分别是35000元和40000元,其中B型单车的成本单价比A型单车高40元,A,B两种单车的成本单价各是多少?(2)、该公司决定采取如下投放方式:甲街区每1000人投放5a辆“共享单车”,乙街区每1000人投放8a辆“共享单车”,按照这种投放方式,甲街区共投放750辆,乙街区共投放600辆.如果两个街区共有75000人,试求a的值.25. 如图,在 中,对角线AC与BD相交于点O,点M,N分别为OB,OD的中点,连接AM并延长至点E,使 ,连接CE,CN. (1)、求证: ;(2)、当AB与AC满足什么数量关系时,四边形MECN是矩形?请说明理由;(3)、连接AN,EN.当 满足什么条件时,四边形MECN是正方形?请说明理由.
(1)、求证: ;(2)、当AB与AC满足什么数量关系时,四边形MECN是矩形?请说明理由;(3)、连接AN,EN.当 满足什么条件时,四边形MECN是正方形?请说明理由.