山东省威海市文登区（鲁教版（五四学制2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-04-01 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各式从左到右的变形中，是因式分解的是（）

A、 $x^{2} - 2 x + 3 = x (x - 2) + 3$ B、 $(x + 4) (x - 4) = x^{2} - 16$ C、 $a^{2} - 2 a b + b^{2} - 1 = {(a - b)}^{2} - 1$ D、 $- 9 + 4 x^{2} = (2 x + 3) (2 x - 3)$

查看试题解析
2. 下列图形中，是中心对称图形但不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 若把分式 $\frac{2 x y}{x - y}$ 中的 $x$ 和 $y$ 都扩大为原来的5倍，那么分式的值（）

A、扩大为原来的5倍 B、扩大为原来的10倍 C、不变 D、缩小为原来的 $\frac{1}{5}$ 倍

查看试题解析
4. 一个多边形的每个外角都等于相邻内角的 $\frac{1}{3}$ ，这个多边形为（）

A、六边形 B、八边形 C、十边形 D、十二边形

查看试题解析
5. 某专卖店专销售某品牌运动鞋，店主对上一周中不同尺码的运动鞋销售情况统计如下：

尺码

40

41

42

43

44

平均每天销售数量/双

5

9

15

8

6

该店主决定本周进货时，增加些42码的运动鞋，影响该店主决策的统计量是（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
6. 下列计算正确的是（）

A、 $\frac{a}{m} + \frac{b}{m} = \frac{a + b}{2 m}$ B、 $a + b \cdot \frac{1}{b} = a$ C、 $\frac{m}{a - b} - \frac{m}{b - a} = 0$ D、 $\frac{x^{2}}{x - 2} - \frac{4 - 4 x}{2 - x} = x - 2$

查看试题解析
7. 若 $x - y = - 3$ ， $x y = 5$ ，则代数式 $2 x^{3} y - 4 x^{2} y^{2} + 2 x y^{3}$ 的值为（）

A、90 B、45 C、-15 D、-30

查看试题解析
8. 某班有46人，一次体能测试后，老师对测试成绩进行了统计．由于小亮没有参加本次集体划试．因此计算其他45人的平均分为88分，方差为38．后来小亮进行了补测，成绩为88分，关于该班46人的测试成绩，下列说法正确的是（）

A、平均分和方差都不变 B、平均分不变，方差变大 C、平均分不变，方差变小 D、平均分和方差都改变

查看试题解析
9. 在平面直角坐标系中，点A ， B ， C的坐标分别为 $(5, 0)$ ， $(- 1, - 3)$ ， $(2, - 5)$ ，当四边形ABCD是平行四边形时，点D的坐标为（）

A、 $(8, - 2)$ B、 $(7, - 3)$ C、 $(8, - 3)$ D、 $(14, 0)$

查看试题解析
10. 如图，在平行四边形ABCD中，点F是AB的中点，连接DF并延长，交CB的延长线于点E ，连接AE ．添加一个条件，使四边形AEBD是菱形，这个条件是（）

A、 $∠ B A D = ∠ B D A$ B、 $A B = D E$ C、 $D F = E F$ D、DE平分 $∠ A D B$

查看试题解析
11. 矩形ABCD与ECFG如图放置，点B ， C ， F共线，点C ， E ， D共线，连接AG ，取AG的中点H，连接EH ．若 $A B = C F = 4$ ， $B C = C E = 2$ ，则 $E H =$ （）

A、 $\sqrt{2}$ B、2 C、 $\sqrt{3}$ D、 $\sqrt{5}$

查看试题解析
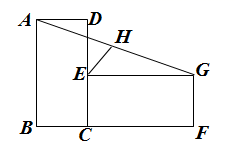12. 如图，在矩形ABCD中，O为AC中点，过点O的直线分别与AB ， CD交于点E、F ，连接BF交AC于点M ，连接DE ， BO ．若 $∠ C O B = 60 °$ ， $F O = F C$ ．则下列结论：①FB垂直平分OC；②四边形DEBF为菱形；③ $O C = F B$ ；④ $A M = 2 B M$ ；⑤ $S_{△ B O M} ： S_{△ A O E} = 3 ： 2$ ．其中正确结论的个数是（）

A、5个 B、4个 C、3个 D、2个

查看试题解析

二、填空题

13. 若关于x的方程 $\frac{3 x - a}{x - 3} = 2 - \frac{a}{3 - x}$ 的解为非负数，则a的取值范围是．

查看试题解析
14. 甲乙两人完成因式分解 $x^{2} + a x + b$ 时，甲看错了a的值，分解的结果是 $(x + 4) (x - 3)$ ，乙看错了b的值，分解的结果为 $(x + 3) (x - 7)$ ，那么 $x^{2} + a x + b$ 分解因式正确的结果为．

查看试题解析
15. 学校倡导全校师生开展“全科阅读”活动，小亮每天坚持读书．原计划用a天读完b页的书，如果要提前m天读完，那么平均每天比原计划要多读页．

查看试题解析
16. 如图，正方形AOBC的两边分别在x轴、y轴上，点 $D (- 4 ， 3)$ 在边AC上，以点B为中心，把△BCD旋转 $90 °$ ，则旋转后点D的对应点 $D_{1}$ 的坐标是．

查看试题解析
17. 如图，在 $△ A B C$ 中， $∠ B A C = 45 °$ ， $A B = A C = 4$ ，点D是AB上一动点，以AC为对角线的所有平行四边形ADCE中，DE的最小值是．

查看试题解析
18. 如图，在平面直角坐标系中，点A ， B ， C的坐标分别为 $(0 ， 1)$ ， $(1 ， 0)$ ， $(- 1 ， 0)$ ，一个电动玩具从坐标原点O出发，第一次跳跃到点 $P_{1}$ ，使得点 $P_{1}$ 与点O关于点A成中心对称；第二次跳跃到点 $P_{2}$ ，使得点 $P_{1}$ 与点 $P_{2}$ 关于点B成中心对称；第三次跳跃到点 $P_{3}$ ，使得点 $P_{3}$ 与点 $P_{2}$ 关于点C成中心对称，第四次跳跃到点 $P_{4}$ ，使得点 $P_{4}$ 与点 $P_{3}$ 关于点A成中心对称；第五次跳跃到点 $P_{5}$ ，使得点 $P_{5}$ 与点 $P_{4}$ 关于点B成中心对称……照此规律重复下去，则点 $P_{2021}$ 的坐标为．

查看试题解析

三、解答题

19. 因式分解：

(1)、 $4 x^{2} - 2 x + \frac{1}{4}$

(2)、 ${(m^{2} + n^{2})}^{2} - 4 m^{2} n^{2}$

查看试题解析
20. 计算：

(1)、 $\frac{2 a + 2}{a^{2} - 1} - \frac{a + 1}{1 - a}$

(2)、 $\frac{x - 2}{x^{2} + 2 x} \div (\frac{2 x - 4}{x + 2} - x + 2)$

(3)、先化简，再求值．
$(\frac{x}{x^{2} + x} - 1) \div \frac{x^{2} - 1}{x^{2} + 2 x + 1}$ ，其中x的值从 $- 1 \leq x < 3$ 中选取一个合适的整数．

查看试题解析

21. 某校为了解学生的身体素质情况，对全校学生进行体能测试，现从七、八两个年级各随机抽取10名学生的成绩（满分为100分）进行调查分析，过程如下：

①收集数据

七年级：90，85.80，95，80，90，80，85，95，100

八年级：90，85，90，80，95，100，90，85，95，100

②整理数据

分数	80	85	90	95	100
七年级人数	3	2	2	2	1
八年级人数	1	2	3	2	a

③分析数据

	平均数	中位数	众数	方差
七年级	88	c	d	e
八年级	b	90	90	39

根据以上信息回答问题：

(1)、直接写出表格中的值：

a =

，

b =

，

c =

，

d =

，

e =

．

(2)、该校七、八年级各有学生800人，本次竞赛成绒不低于90分的为“优秀”，估计这两个年级共有多少名学生达到“优秀”？

查看试题解析

22. 如图所示，在正方形网格中， $△ A B C$ 的顶点坐标分别为 $(2 ， 4)$ ， $(1 ， 2)$ ， $(4 ， 1)$ ．请在所给直角坐标系中按要求画图和解答下列问题：

(1)、以点P为旋转中心，将 $△ A B C$ 按逆时针方向旋转 $90 °$ 得到 $△ A^{'} B^{'} C^{'}$ ，请在图中画出 $△ A^{'} B^{'} C^{'}$ ，并写出点B的对应点 $B^{'}$ 的坐标为．

(2)、在y轴上求作一点M ，使 $M A + M B$ 的值最小，点M的坐标为．

查看试题解析
23. 某市在精致城市建设过程中，需铺设一条长度为900米的管道．决定由甲工程队来完成这一工程，为加快施工进程，甲工程队引进了新设备，实际每天铺设管道长度比原计划增加了50%，结果比原计划少用2天完成任务．求甲工程队实际每天铺设管道多少米？

查看试题解析
24. $△ A B C$ ，点M为射线CD上任意一点（点M与点C不重合）．连接BM ，将线段BM绕点B逆时针旋转得到线段BN ，连接NA并延长，交直线CD于点E ．

(1)、如图1， $△ A B C$ 是等边三角形，将线段BM绕点B逆时针旋转 $60 °$ 得到线段BN ，猜想 $∠ M E N$ 的度数，并证明．

(2)、如图2，若 $∠ B A C = ∠ B C = 50 °$ ，将线段BM绕点B逆时针旋转 $80 °$ 得到线段BN ，猜想 $∠ M E N$ 的度数，并证明．

查看试题解析
25. 如图1，点E是正方形ABCD边AB上任意一点，以BE为边作正方形BEFG ，连接DF ，点M ， N分别是线段AE、DF中点，连接MN ．

(1)、请猜想MN与AE的关系，并证明你的结论；

(2)、把图1中的正方形BEFG绕点B顺时针旋转 $90 °$ ，此时点E、G恰好分别落在线段BC、AB上，如图2，其他条件不变，（1）中的结论是否成立？请说明理由．

查看试题解析

尺码	40	41	42	43	44
平均每天销售数量/双	5	9	15	8	6