初中数学湘教版八年级下学期期中复习专题8 矩形的性质与判定
试卷更新日期:2021-04-01 类型:复习试卷
一、单选题
-
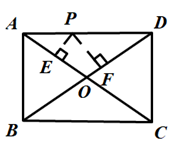
1. 下列四边形对角线相等但不一定垂直的是( )A、矩形 B、平行四边形 C、菱形 D、正方形2. 矩形具有而平行四边形不具有的性质是( )A、对角线相等 B、两组对边分别平行 C、对角线互相平分 D、两组对角分别相等3. 如图,P是矩形ABCD的边AD上一个动点,矩形的两条边AB、BC的长分别为6和8,那么点P到矩形的两条对角线AC和BD的距离之和是( )
 A、 B、 C、 D、无法确定4. 如图,矩形ABCD的对角线交于点O.若∠BAO=55°,则∠AOD等于( )
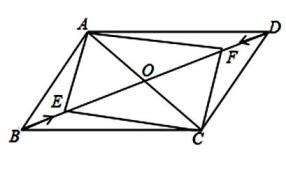
A、 B、 C、 D、无法确定4. 如图,矩形ABCD的对角线交于点O.若∠BAO=55°,则∠AOD等于( )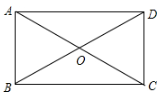 A、110° B、115° C、120° D、125°5. 矩形的一内角平分线把矩形的一条边分成2和3两部分,则该矩形的周长是( ).A、12 B、14 C、16 D、14或166. 如果依次连接四边形各边的中点所得四边形是矩形,那么原来的四边形的两条对角线( )A、相等 B、互相垂直 C、互相平分 D、互相平分且相等7. 在四边形ABCD中,对角线 互相平分,若添加一个条件使得四边形ABCD是矩形,则这个条件可以是( )A、 B、 C、 D、8. 下列命题中,真命题是( )A、对角线互相平分且相等的四边形是矩形 B、对角线互相垂直且相等的四边形是矩形 C、对角线互相平分的四边形是矩形 D、对角线互相垂直的四边形是矩形9. 在数学活动课上,老师让同学们判定一个四边形门框是否为矩形,下面是某合作小组的四位同学的拟订方案,其中正确的是( )A、测量对角线是否互相平分 B、测量两组对边是否分别相等 C、测量一组对角是否为直角 D、测量两组对边是否相等,再测量对角线是否相等10. 如图,四边形ABCD的对角线AC,BD相交于点O,已知下列6个条件:①AB∥DC;②AB=DC;③AC=BD;④∠ABC=90°;⑤OA=OC;⑥OB=OD.则不能使四边形ABCD成为矩形的是( )
A、110° B、115° C、120° D、125°5. 矩形的一内角平分线把矩形的一条边分成2和3两部分,则该矩形的周长是( ).A、12 B、14 C、16 D、14或166. 如果依次连接四边形各边的中点所得四边形是矩形,那么原来的四边形的两条对角线( )A、相等 B、互相垂直 C、互相平分 D、互相平分且相等7. 在四边形ABCD中,对角线 互相平分,若添加一个条件使得四边形ABCD是矩形,则这个条件可以是( )A、 B、 C、 D、8. 下列命题中,真命题是( )A、对角线互相平分且相等的四边形是矩形 B、对角线互相垂直且相等的四边形是矩形 C、对角线互相平分的四边形是矩形 D、对角线互相垂直的四边形是矩形9. 在数学活动课上,老师让同学们判定一个四边形门框是否为矩形,下面是某合作小组的四位同学的拟订方案,其中正确的是( )A、测量对角线是否互相平分 B、测量两组对边是否分别相等 C、测量一组对角是否为直角 D、测量两组对边是否相等,再测量对角线是否相等10. 如图,四边形ABCD的对角线AC,BD相交于点O,已知下列6个条件:①AB∥DC;②AB=DC;③AC=BD;④∠ABC=90°;⑤OA=OC;⑥OB=OD.则不能使四边形ABCD成为矩形的是( )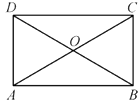 A、①②③ B、②③④ C、②⑤⑥ D、④⑤⑥
A、①②③ B、②③④ C、②⑤⑥ D、④⑤⑥二、填空题
-
11. 在矩形ABCD中,AC与BD相交于点O,若OA=2,则BD的长是.12. 在矩形 中, 与 相交于点 , ,那么 的度数为, .13. 如图,在四边形ABCD中,已知AB∥DC,AB=DC. 在不添加任何辅助线的前提下,要想该四边形成为矩形,只需再加上的一个条件是 .
 14. 在平行四边形 中,若再增加一个条件 , 使平行四边形 能成为矩形(填写一个你认为正确的即可).
14. 在平行四边形 中,若再增加一个条件 , 使平行四边形 能成为矩形(填写一个你认为正确的即可).
15. 在四边形ABCD中,对角线AC , BD交于点O且AC , BD互相平分,若添加一个条件使得四边形ABCD是矩形,则这个条件可以是(填写一个即可).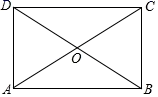
三、解答题
-
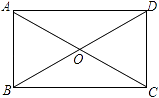
16. 如图,矩形ABCD中,AC与BD相交于点O.若 AO=3,∠OBC=30°,求矩形的周长和面积.
 17. 如图,O是矩形ABCD的对角线的交点,DE∥AC,CE∥BD,DE和CE相交于E,求证:四边形OCED是菱形。
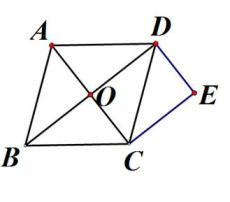
17. 如图,O是矩形ABCD的对角线的交点,DE∥AC,CE∥BD,DE和CE相交于E,求证:四边形OCED是菱形。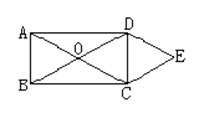 18. 如图,菱形ABCD的对角线AC、BD相交于点O,过点D、C分别作AC、BD的平行线,交于点E.
18. 如图,菱形ABCD的对角线AC、BD相交于点O,过点D、C分别作AC、BD的平行线,交于点E.求证:四边形ODEC为矩形;
 19. 已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,若MA=MC,∠BAN=90°,求证:四边形ADCN是矩形.
19. 已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,若MA=MC,∠BAN=90°,求证:四边形ADCN是矩形.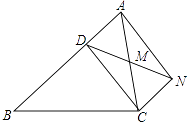
四、综合题
-
20. 如图所示,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作BE的平行线与线段ED的延长线交于点F,连结AE、CF.
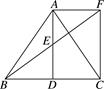
 (1)、求证:AF=CE;(2)、若AC=EF,试判断四边形AFCE是什么样的四边形,并证明你的结论.21. 如图,在等边三角形ABC中,点D是BC边的中点,以AD为边作等边三角形ADE.
(1)、求证:AF=CE;(2)、若AC=EF,试判断四边形AFCE是什么样的四边形,并证明你的结论.21. 如图,在等边三角形ABC中,点D是BC边的中点,以AD为边作等边三角形ADE.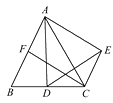 (1)、求∠CAE的度数;(2)、取AB边的中点F,连结CF、CE,试证明四边形AFCE是矩形.
(1)、求∠CAE的度数;(2)、取AB边的中点F,连结CF、CE,试证明四边形AFCE是矩形.