山东省临沂市兰陵县2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-04-01 类型：期末考试

进入出卷网下载

一、单选题

1. 自新冠肺炎疫情发生以来，全国人民共同抗疫，各地积极普及科学防控知识.下面是科学防控知识的图片，图片上有图案和文字说明，其中的图案是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列计算正确的是（）

A、a⁶÷a²=a⁴ B、（2a²）³=6a⁶ C、（a²）³=a⁵ D、（a+b）²=a²+b²

查看试题解析
3. 如图， $△ A B C$ 中， $∠ A = 60^{°} ， ∠ B = 40^{°} ， D E / / B C$ ，则 $∠ A E D$ 的度数是（）

A、50° B、60° C、70° D、80°

查看试题解析
4. 下列运算正确的是（）

A、 $\frac{a}{m} + \frac{b}{m} = \frac{a + b}{2 m}$ B、 $\frac{a}{x - y} - \frac{a}{y - x} = 0$ C、 $1 + \frac{1}{a} = \frac{2}{a}$ D、 $\frac{x}{x + y} + \frac{y}{y + x} = 1$

查看试题解析
5. 式子 $3 x^{2} y - 3 y$ 因式分解的最后结果是（）

A、 $3 y (x - 1) (x + 1)$ B、 $3 (x^{2} y - y)$ C、 $3 y (x^{2} - 1)$ D、 $y (3 x^{2} - 3)$

查看试题解析
6. 已知 $a$ ， $b$ ， $c$ 为 $△ A B C$ 的三边长，且满足 $a c + b c = b^{2} + a b$ ，则 $△ A B C$ 的形状是（）

A、等边三角形 B、直角三角形 C、等腰直角三角形 D、等腰三角形

查看试题解析
7. 如图，在 $△ A B C$ 中， $∠ A = 30 °$ ， $∠ B = 50 °$ ， $C D$ 平分 $∠ A C B$ ，则 $∠ A D C$ 的度数是（）

A、 $80 °$ B、 $90 °$ C、 $100 °$ D、 $110 °$

查看试题解析
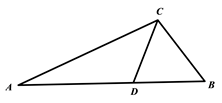8. 市某视力健康管理中心对全市初中生的视力情况进行了一次抽样调查，如图是利用调查所得数据绘制的频数直方图，则这组数据的组数与组距分别是（）

A、4和0.20 B、4和0.30 C、5和0.20 D、5和0.30

查看试题解析
9. 一个多边形的内角和是外角和的2倍，则这个多边形对角线的条数是（）

A、3 B、4 C、9 D、18

查看试题解析
10. 甲、乙两人加工某种机器零件，已知每小时甲比乙少加工6个这种零件，甲加工240个这种零件所用的时间与乙加工300个这种零件所用的时间相等，设甲每小时加工x个零件，所列方程正确的是（）

A、 $\frac{240}{x} = \frac{300}{x - 6}$ B、 $\frac{240}{x} = \frac{300}{x + 6}$ C、 $\frac{240}{x - 6} = \frac{300}{x}$ D、 $\frac{240}{x + 6} = \frac{300}{x}$

查看试题解析
11. 若a + b = 3,ab = 4 ,则 $\frac{b}{a} + \frac{a}{b}$ 的值是（）

A、 $\frac{1}{4}$ B、 $\frac{3}{4}$ C、 $\frac{9}{4}$ D、 $\frac{17}{4}$

查看试题解析
12. 如图， $A D$ 是 $△ A B C$ 的中线， $E$ ， $F$ 分别是 $A D$ 和 $A D$ 延长线上的点，且 $D E = D F$ ，连接 $B F$ ， $C E$ ，下列说法：① $△ A B D$ 和 $△ A C D$ 面积相等； ② $∠ B A D = ∠ C A D$ ； ③ $△ B D F$ ≌ $△ C D E$ ；④ $B F / / C E$ ；⑤ $C E = A E$ ．其中正确的是（）

A、①② B、①③ C、①③④ D、①④⑤

查看试题解析
13. 如图， $Δ A B C$ 中， $A B = A C$ ， $B C = 3$ ， $S_{Δ A B C} = 6$ ， $A D ⊥ B C$ 于点 $D$ ， $E F$ 是 $A B$ 的垂直平分线，交 $A B$ 于点 $E$ ，交 $A C$ 于点 $F$ ，在 $E F$ 上确定一点 $P$ ，使 $P B + P D$ 最小，则这个最小值为（）

A、3.5 B、4 C、4.5 D、5

查看试题解析
14. 如果 $a$ ， $b$ ， $c$ 是正数，且满足 $a + b + c = 1$ ， $\frac{1}{a + b} + \frac{1}{b + c} + \frac{1}{a + c} = 5$ ，那么 $\frac{c}{a + b} + \frac{a}{b + c} + \frac{b}{a + c}$ 的值为（）

A、-1 B、1 C、2 D、 $\frac{1}{2}$

查看试题解析

二、填空题

15. 计算： ${(- 4)}^{2020} \times {0.25}^{2019} =$ ．

查看试题解析
16. 已知3a-b=0,则分式 $\frac{a + b}{b}$ 的值为

查看试题解析
17. 如图，在等边 $Δ A B C$ 中，将 $∠ C$ 沿虚线 $D E$ 剪去，则 $∠ A D E + ∠ D E B =$ °．

查看试题解析
18. 如图， $A B ∥ C D$ ，以点 $A$ 为圆心，小于 $A C$ 长为半径画弧，分别交 $A B$ ， $A C$ 于 $E$ ， $F$ 两点，再分别以 $E$ ， $F$ 为圆心，大于 $\frac{1}{2} E F$ 长为半径画弧，两弧交于点 $P$ ，作射线 $A P$ ，交 $C D$ 于点 $M$ .若 $∠ C = 150 °$ ，则 $∠ C M A$ 的大小等于（度）.

查看试题解析
19. 如图， $A D$ 平分 $∠ B A C$ ， $D E ⊥ A C$ ，垂足为 $E$ ， $B F / / A C$ 交 $E D$ 的延长线于点 $F$ ，若 $B C$ 恰好平分 $∠ A B F$ ．则下列结论中：
① $A D$ 是 $Δ A B C$ 的高；

② $Δ A B C$ 是等边三角形；

③ $E D = F D$ ；

④ $A B = A E + B F$ ．

其中正确的是（填写序号）

查看试题解析

三、解答题

20. 先化简，再求值： $\frac{x^{2} - 1}{x^{2} + 2 x + 1} \div (1 - \frac{1}{x + 1})$ ，其中 $x = 2$ ．

查看试题解析
21. 随着科技的迅猛发展，高铁已成为我国制造业的一张名片，享誉全球．近几年来，我国高铁科研团队继续深入研究、革新技术，某次列车平均提速v km/h ，用相同的时间，列车提速前行驶s km，提速后比提速前多行驶50 km，提速前列车的平均速度为多少？

查看试题解析
22. 如图，在 $△ A B C$ 中，点D是边 $B C$ 上一点， $C D = A B$ ，点E在边 $A C$ 上，且 $A D = D E$ ， $∠ B A D = ∠ C D E$ ．

(1)、如图1，求证： $B D = C E$ ；

(2)、如图2，若 $D E$ 平分 $∠ A D C$ ，在不添加辅助线的情况下，请直接写出图中所有与 $∠ A D E$ 相等的角（ $∠ A D E$ 除外）．

查看试题解析
23. 如图，已知点 $B$ ， $C$ ， $D$ 在同一条直线上， $Δ A B C$ 和 $Δ C D E$ 都是等边三角形，连接 $B E$ ， $A D$ ． $B E$ 交 $A C$ 于点 $F$ ， $A D$ 交 $C E$ 于点 $H$ ．连接 $F H$ ．

(1)、求证： $B E = A D$ ；

(2)、判断 $Δ C F H$ 的形状，并说明理由．

查看试题解析
24. 如图， $Δ A B C$ 是等边三角形， $Δ A D C$ 与 $Δ A B C$ 关于直线 $A C$ 对称， $A E$ ⊥ $C D$ 交 $B C$ 的延长线于点 $E$ ， $∠ E A F = 45 °$ ，且 $A F$ 与 $A B$ 在 $A E$ 的两侧， $E F ⊥ A F$ ．

(1)、作图：依题意补全图形；

(2)、在 $A E$ 上找一点 $P$ ，使点 $P$ 到点 $B$ ，点 $C$ 的距离的和最短（作图并写出作法）；

(3)、求证：点 $D$ 到 $A F$ ， $E F$ 的距离相等．

查看试题解析