山东省临沂市莒南县2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-04-01 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图标中，不是轴对称图形的是（）．

A、 B、 C、 D、

查看试题解析
2. 若代数式 $\frac{2 x - 4}{x - 5}$ 有意义，则实数 x 的取值范围是（）

A、x = 5 B、x = 2 C、x ≠5 D、x ≠2

查看试题解析
3. 已知三角形的两边长分别是4和9，则此三角形第三条边的长可能是（）

A、3 B、4 C、6 D、15

查看试题解析
4. 下列运算正确的是（）

A、（x²）³＋（x³）²＝2x⁶ B、（x²）³·（x²）³＝2x¹² C、x⁴·（2x）²＝2x⁶ D、（2x）³·（-x）²＝﹣8x⁵

查看试题解析
5. 下列因式分解正确的是（）

A、a⁴b﹣6a³b＋9a²b＝a²b（a²﹣6a＋9） B、x²﹣x＋ $\frac{1}{4}$ ＝（x﹣ $\frac{1}{2}$ ）² C、x²﹣2x＋4＝（x﹣2）² D、x²﹣4＝（x＋4）（x﹣4）

查看试题解析
6.
如图，直线l外不重合的两点A、B，在直线l上求作一点C，使得AC+BC的长度最短，作法为：①作点B关于直线l的对称点B′；②连接AB′与直线l相交于点C，则点C为所求作的点．在解决这个问题时没有运用到的知识或方法是（）

A、转化思想 B、三角形的两边之和大于第三边 C、两点之间，线段最短 D、三角形的一个外角大于与它不相邻的任意一个内角

查看试题解析
7. 多项式 $m x^{2} - m$ 与多项式 $x^{2} - 2 x + 1$ 的公因式是（）

A、 $x - 1$ B、 $x + 1$ C、 $x^{2} - 1$ D、 ${(x - 1)}^{2}$

查看试题解析
8. 如图，已知D为△ABC边AB的中点，E在AC上，将△ABC沿着DE折叠，使A点落在BC上的F处．若∠B=65°，则∠BDF等于（）

A、65° B、50° C、60° D、57.5°

查看试题解析
9. 已知关于 $x$ 的分式方程 $\frac{x}{x - 3} - 4 = \frac{k}{3 - x}$ 的解为非正数，则 $k$ 的取值范围是（）

A、 $k \leq - 12$ B、 $k \geq - 12$ C、 $k > - 12$ D、 $k < - 12$

查看试题解析
10. 如图，Rt△ABC中，∠C=90°，AD平分∠BAC，交BC于点D，AB=10，S_△_ABD=15，则CD的长为（）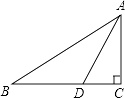

A、3 B、4 C、5 D、6

查看试题解析
11. 已知 $x^{m} = 4, x^{n} = 6$ ，则 $x^{2 m - n}$ 的值为（）

A、9 B、 $\frac{3}{4}$ C、 $\frac{8}{3}$ D、 $\frac{4}{3}$

查看试题解析
12. 已知：如图，在△ABC与△AEF中，点F在BC上，AB=AE ， BC=EF ， ∠B=∠E ， AB交EF于点D ．下列结论：①∠EAB=∠FAC；②AF=AC；③FA平分∠EFC；④∠BFE=∠FAC中，正确的有（）个．

A、1 B、2 C、3 D、4

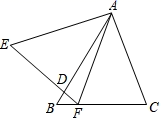查看试题解析
13. 如图，在 $△ A B C$ 中，AB＝AC，分别以点A、B为圆心，以适当的长为半径作弧，两弧分别交于E，F，作直线EF，D为BC的中点，M为直线EF上任意一点.若BC＝4， $△ A B C$ 面积为10，则BM+MD长度的最小值为（）

A、 $\frac{5}{2}$ B、3 C、4 D、5

查看试题解析
14. 如图：△ABC是等边三角形，AE＝CD，AD，BE相交于点P，BQ⊥AD于Q，PQ＝4，PE＝1，则AD的长是（）

A、9 B、8 C、7 D、6

查看试题解析

二、填空题

15. 2020年1月24日，中国疾控中心成功分离我国首株新型冠状病毒毒种，该毒种直径大约为90纳米（1纳米＝0.000001毫米），数据“90纳米”用科学记数法表示为毫米．

查看试题解析
16. 已知点P（3，a）关于y轴的对称点为Q（b，2），则ab= ．

查看试题解析
17. 关于x的分式方程 $\frac{m}{x^{2} - 4}$ - $\frac{1}{x + 2}$ =0无解，则m=.

查看试题解析
18. 若a²＋2ab＋b²﹣c²＝10，a＋b＋c＝5，则a＋b﹣c的值是．

查看试题解析
19. 课间，小聪拿着老师的等腰直角三角板玩，不小心掉到两墙之间（如图）， $∠ A C B = 90 °$ ， $A C = B C$ ，每块砌墙用的砖块厚度为8cm，小聪很快就知道了两个墙脚之间的距离 $D E$ 的长为cm

查看试题解析

三、解答题

20. 计算：

(1)、（﹣1）²⁰¹⁹＋（ $\frac{1}{2}$ ）^﹣2﹣（3.14﹣π）⁰

(2)、（a＋3）²﹣（a＋1）（a﹣1）﹣2（2a＋4）．

查看试题解析
21.

(1)、因式分解：3xy³﹣6x²y²＋3x³y．

(2)、解分式方程： $\frac{x - 2}{2 x - 1}$ ＋1＝﹣ $\frac{3}{4 x - 2}$ ．

查看试题解析
22. 先化简： $(\frac{x + 1}{x - 1} + 1) \div \frac{x^{2} + x}{x^{2} - 2 x + 1} + \frac{2 - 2 x}{x^{2} - 1}$ ，然后从﹣2≤x≤2的范围内选取一个合适的整数作为x的值代入求值．

查看试题解析
23. 某内陆城市为了落实国家“一带一路”战略，促进经济发展，增强对外贸易的竞争力，把距离港口420 km的普通公路升级成了同等长度的高速公路，结果汽车行驶的平均速度比原来提高了50%，行驶时间缩短了2 h，求汽车原来的平均速度．

查看试题解析
24. 等边△ABC中，AO是BC边上的高，D为AO上一点，以CD为一边，在CD下方作等边△CDE，连接BE．

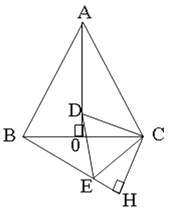(1)、求证：△ACD≌△BCE

(2)、过点C作CH⊥BE，交BE的延长线于H，若BC=8，求CH的长．

查看试题解析
25. 图1是一个长为2m，宽为2n的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图2的形状拼成一个正方形．

(1)、图2中的阴影部分的正方形的边长等于．

(2)、观察图2你能写出下列三个代数式（m＋n）² ，（m﹣n）² ， mn之间的等量关系．

(3)、运用你所得到的公式，计算若mn＝﹣2，m﹣n＝4，求：
①（m＋n）²的值．

②m⁴＋n⁴的值．

(4)、用完全平方公式和非负数的性质求代数式x²＋2x＋y²﹣4y＋7的最小值．

查看试题解析
26. 在△DEF中，DE＝DF，点B在EF边上，且∠EBD＝60°，C是射线BD上的一个动点（不与点B重合，且BC≠BE），在射线BE上截取BA＝BC，连接AC．

(1)、当点C在线段BD上时，
①若点C与点D重合，请根据题意补全图1，并直接写出线段AE与BF的数量关系为 ▲ ；

②如图2，若点C不与点D重合，请证明AE＝BF＋CD；

(2)、当点C在线段BD的延长线上时，用等式表示线段AE，BF，CD之间的数量关系（直接写出结果，不需要证明）．

查看试题解析