江西省吉安市遂川县2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-04-01 类型：期末考试

进入出卷网下载

一、单选题

1. -8的立方根是（）

A、-3 B、-2 C、2 D、3

查看试题解析
2. 如图， $A B / / C D$ ， $C E$ 平分 $∠ B C D$ ， $∠ B = 36 °$ ，则 $∠ D C E$ 等于（）

A、 $18 °$ B、 $36 °$ C、 $45 °$ D、 $54 °$

查看试题解析
3. 若点 $A (a - 3, a + 4)$ 在 $y$ 轴上，则点 $B (- a, - a + 3)$ 在（）

A、第二象限 B、第三象限 C、 $x$ 轴上 D、 $y$ 轴上

查看试题解析
4. 下列长度的三条线段能组成钝角三角形的是（）

A、2，4， $\sqrt{3}$ B、6，8，10 C、 $2 \sqrt{2}$ ，2，2 D、5，4，6

查看试题解析
5. 已知方程组 ${\begin{array}{l} 2 x + y = 3 \\ x - 2 y = 5 \end{array}$ ，则 $x + 3 y$ 的值是（）

A、-1 B、1 C、-2 D、2

查看试题解析
6. 无论k为何值，一次函数 $y = k x + k - 2$ 的图象总是经过某一个确定的点，这个点的坐标为（）

A、 $(1, - 2)$ B、 $(- 1, 2)$ C、 $(1, 2)$ D、 $(- 1, - 2)$

查看试题解析

二、填空题

7. 已知正比例函数 $y = 3 x$ 的图象经过点 $(1, m)$ ，则 $m$ 的值为．

查看试题解析
8. $\sqrt{7}$ 最接近的整数是．

查看试题解析
9. 若方程组 ${\begin{array}{l} a x + y = 5 \\ x - b y = - 1 \end{array}$ 的解为 ${\begin{array}{l} x = 2 \\ y = - 1 \end{array}$ ，则a+b的值为．

查看试题解析
10. 若一组数据2，0，3，4，6， $x$ 的众数为4，则这组数据的中位数是．

查看试题解析
11. 如图， $A B / / C D$ ， $∠ A = 49 °$ ， $∠ C = 25 °$ ，则 $∠ E$ 的度数为．

查看试题解析
12. 在平面直角坐标系中，一次函数 $y = x + 4$ 的图象分别与 $x$ 轴， $y$ 轴交于点 $A$ ， $B$ ，点 $P$ 在一次函数 $y = x$ 的图象上，则当 $Δ A B P$ 为直角三角形时，点 $P$ 的坐标是．

查看试题解析

三、解答题

13.

(1)、计算： $\frac{\sqrt{8} + \sqrt{18}}{5} \times \sqrt{\frac{1}{2}}$ ；

(2)、如图，已知 $a / / b$ ，把三角板的直角顶点放在直线 $b$ 上．若 $∠ 1 = 40 °$ ，求 $∠ 2$ 的度数．

查看试题解析
14. 解方程组 ${\begin{matrix} x - y = 8 \\ 3 x + y = 12 \end{matrix}$ ．

查看试题解析
15. 如图，已知在Rt△ABC中，∠C＝90°，AC＝9，BC＝12，求点C到AB的距离.

查看试题解析
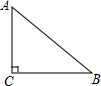16. 如图，是由边长为1的小正方形组成的 $7 \times 6$ 的网格， $Δ A B C$ 的顶点都在格点上，

请仅用无刻度的直尺作图．

(1)、作 $Δ A B C$ 的角平分线 $B D$ ；

(2)、在网格中确定一个格点 $P$ ，作 $∠ A B P = 45 °$ ．

查看试题解析
17. 某校食堂的中餐与晚餐的消费标准如表

种类

单价

米饭

0.5元/份

A类套餐菜

3.5元/份

B类套餐菜

2.5元/份

一学生某星期从周一到周五每天的中餐与晚餐均在学校用餐，每次用餐米饭选1份，A、B类套餐菜选其中一份，这5天共消费36元，请问这位学生A、B类套餐菜各选用多少次？

查看试题解析
18. 如图，直线 $A B$ 与 $x$ 轴， $y$ 轴分别交于点 $A (- 8 ， 0)$ ， $B (0 ， 6)$ ．

(1)、求直线 $A B$ 的函数表达式；

(2)、若点 $C$ 的坐标为 $(- 6 ， 0)$ ，点 $P (m ， n)$ 在线段 $A B$ 上（不与点 $A$ 重合），求 $Δ O P C$ 的面积 $S$ 与 $m$ 的函数关系式，并直接写出自变量的取值范围．

查看试题解析

19. 2020年是全面建成小康社会目标实现之年，是全面打赢脱贫攻坚战收官之年．为了让老师们更好地了解国家的宏观政策及具体措施，某学校领导组织全体教师利用“学习强国

A P P

”对相关知识进行学习并组织定时测试（总分为100分）．现从该校中随机抽取20名教师的测试成绩进行分析，过程如下：

收集数据20名教师的测试成绩如下（单位：分）

76，83，71，100，81，100.82，88， 95 , 90，

100，86，89，93，86，100，96，100，92，90

(1)、整理数据

请你按如下表格分组整理、描述样本数据，并把下列表格补充完整．

成绩（个）	$0 \leq x < 60$	$60 \leq x < 70$	$70 \leq x < 80$	$80 \leq x < 90$	$90 \leq x < 100$
等级	$A$	$B$	$C$	$D$	$E$
人数	0

分析数据请将下列表格补充完整

平均数	中位数	满分率
91.9		25%

(2)、得出结论

用样本中的统计量估计全校教师的测试成绩等级为；

(3)、若该校共有教师210人，请估计该校教师的测试成绩等级为

D

，

E

的总人数．

查看试题解析

20. 如图，在平面直角坐标系中，四边形 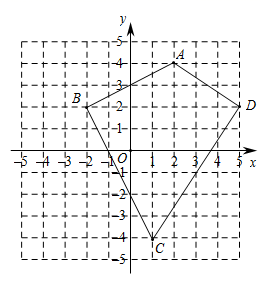$A B C D$ 的顶点 $A$ 的坐标为 $(2 ， 4)$ ．

(1)、直接写出其他顶点坐标为 $B$ ， $C$ ， $D$ ；

(2)、将四边形向左平移，要使其对角线 $B D$ 的中点落在 $y$ 轴上，平移的距离应为；

(3)、求对角线 $A C$ 的长．

查看试题解析
21. 先观察下列各组数，然后回答问题：
第一组：1， $\sqrt{3}$ ，2；第二组： $\sqrt{2}$ ，2， $\sqrt{6}$ ；

第三组： $\sqrt{3}$ ， $\sqrt{5}$ ， $\sqrt{8}$ ；第四组：2， $\sqrt{6}$ ， $\sqrt{10}$ ；

$\dots \dots$

(1)、根据各组数反映的规律，用含 $n$ 的代数式表示第 $n$ 组的三个数；

(2)、如果各组数的三个数分别是三角形的三边长，那么这个三角形是什么三角形？请说明理由；

(3)、如图， $C B = 3$ ， $A B = m$ ， $A C = n$ ，若3， $m$ ， $n$ 为上列按已知方式排列顺序的某一组数，且 $∠ D A B = 90 °$ ， $A D = A C$ ，求 $B D$ 的长．

查看试题解析
22. 如图1，点A、B分别在射线 $O M$ 、 $O N$ 上运动（不与点O重台）， $A C$ 、 $B C$ 分别是 $∠ B A O$ 和 $∠ A B O$ 的角平分线， $B C$ 延长线交 $O M$ 于点G ．

(1)、若 $∠ M O N = 60^{\circ}$ ，则 $∠ A C G =$ ；（直接写出答案）

(2)、若 $∠ M O N = n^{\circ}$ ，求出 $∠ A C G$ 的度数；（用含n的代数式表示）

(3)、如图2．若 $∠ M O N = 80^{\circ}$ ，过点C作 $C F // O A$ 交 $A B$ 于点F ，求 $∠ B G O$ 与 $∠ A C F$ 数量关系．

查看试题解析
23. 如图，在平面直角坐标系中，一次函数 $y = - 2 x + 4$ 图象与坐标轴分别交于点 $A (a ， 0)$ ， $B (0 ， b)$ ．

(1)、 $A$ 点的坐标为， $B$ 点的坐标为；

(2)、若 $M$ 为直线 $y = m x (m > 0)$ 在第一象限上一点，连接 $M A$ ， $M B$ ．
①当 $m = 1$ 时， $Δ A B M$ 是以 $A B$ 为底的等腰直角三角形，求点 $M$ 的坐标；

②当 $m \neq 1$ 时，是否仍然存在 $Δ A B M$ 是以 $A B$ 为底的等腰直角三角形的情况？如果存在，求此时点 $M$ 的坐标；如果不存在，说明理由；

③当 $Δ A B M$ 是以 $A B$ 为底的等腰三角形，且为锐角三角形时，直接写出 $m$ 的取值范围．

查看试题解析

种类	单价
米饭	0.5元/份
A类套餐菜	3.5元/份
B类套餐菜	2.5元/份