江西省吉安市吉水县2020-2021学年八年级上学期数学期末试卷
试卷更新日期:2021-04-01 类型:期末考试
一、单选题
-
1. 在直角坐标中,点P(2,﹣3)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 实数 ,0,﹣π, , 中无理数的个数是( )A、1 B、2 C、3 D、43. 下列命题中,是假命题的是( )A、两直线平行,则同位角相等 B、同旁内角互补,则两直线平行 C、三角形内角和为180° D、三角形一个外角大于任何一个内角4. 有一道题目:已知一次函数y=2x+b,其中b<0,…,与这段描述相符的函数图象可能是( )A、
 B、
B、 C、
C、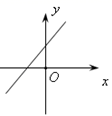 D、
D、 5. 下列数据中不能作为直角三角形的三边长是( )A、1、1、 B、5、12、13 C、3、5、7 D、6、8、106. 如图,下列条件不能判断直线a∥b的是( )
5. 下列数据中不能作为直角三角形的三边长是( )A、1、1、 B、5、12、13 C、3、5、7 D、6、8、106. 如图,下列条件不能判断直线a∥b的是( ) A、∠1=∠4 B、∠3=∠5 C、∠2+∠5=180° D、∠2+∠4=180°
A、∠1=∠4 B、∠3=∠5 C、∠2+∠5=180° D、∠2+∠4=180°二、填空题
-
7. 计算: =
8. 甲、乙两名同学投掷实心球,每人投10次,平均成绩为7米,方差分别为; S甲2=0.1,S乙2=0.04,成绩比较稳定的是 .9. 写出二元一次方程x+4y=11的一个整数解 .10. 将一副三角板,按如图方式叠放,那么 的度数是 . 11. 如图,已知直线y=ax+b和直线y=kx交于点P,则关于x,y的二元一次方程组 的解是 .
11. 如图,已知直线y=ax+b和直线y=kx交于点P,则关于x,y的二元一次方程组 的解是 . 12. 如图,已知一次函数y=﹣x+1的图象与x轴、y轴分别交于点A , B , 点M在y轴上(M不与原点重合),并且使以点A , B , M为顶点的三角形是等腰三角形,则M的坐标为 .
12. 如图,已知一次函数y=﹣x+1的图象与x轴、y轴分别交于点A , B , 点M在y轴上(M不与原点重合),并且使以点A , B , M为顶点的三角形是等腰三角形,则M的坐标为 .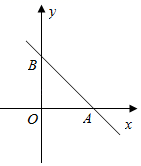 13. x﹣2的平方根是±2,2x+y+7的立方根是3,求x2+y2的平方根 .
13. x﹣2的平方根是±2,2x+y+7的立方根是3,求x2+y2的平方根 .三、解答题
-
14.(1)、计算: ;(2)、解方程组: .15. 已知y+1与x﹣1成正比,且当x=3时y=﹣5,请求出y关于x的函数表达式,并求出当y=5时x的值.16. 已知在平面直角坐标系中
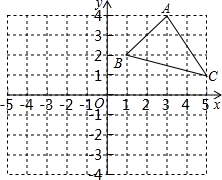 (1)、画出△ABC关于x轴成轴对称图形的三角形A′B′C′;(2)、写出A′,B′,C′的坐标.17. 如图,已知:CF⊥AB于F,ED⊥AB于D,∠1=∠2,求证:FG∥BC.
(1)、画出△ABC关于x轴成轴对称图形的三角形A′B′C′;(2)、写出A′,B′,C′的坐标.17. 如图,已知:CF⊥AB于F,ED⊥AB于D,∠1=∠2,求证:FG∥BC. 18. 我市为加快美丽乡村建设,建设秀美幸福抚州,对A、B两类村庄进行了全面改建.根据预算,建设一个A类美丽村庄和一个B类美丽村庄共需资金300万元;甲镇建设了2个A类村庄和5个B类村庄共投入资金1140万元.(1)、建设一个A类美丽村庄和一个B类美丽村庄所需的资金分别是多少万元?(2)、乙镇3个A类美丽村庄和4个B类村庄改建共需资金多少万元?19. 某校260名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了若干名学生每人的植树量,并分为四种类型, :4棵; :5棵; :6棵; :7棵;将各类的人数绘制成扇形图(如图1)和条形图(如图2).回答下列问题:
18. 我市为加快美丽乡村建设,建设秀美幸福抚州,对A、B两类村庄进行了全面改建.根据预算,建设一个A类美丽村庄和一个B类美丽村庄共需资金300万元;甲镇建设了2个A类村庄和5个B类村庄共投入资金1140万元.(1)、建设一个A类美丽村庄和一个B类美丽村庄所需的资金分别是多少万元?(2)、乙镇3个A类美丽村庄和4个B类村庄改建共需资金多少万元?19. 某校260名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了若干名学生每人的植树量,并分为四种类型, :4棵; :5棵; :6棵; :7棵;将各类的人数绘制成扇形图(如图1)和条形图(如图2).回答下列问题: (1)、在这次调查中D类型有多少名学生?(并在图中画出)(2)、写出被调查学生每人植树量的众数、中位数;(3)、求被调查学生每人植树量的平均数,并估计这260名学生共植树多少棵?20. 如图,在四边形ABCD中,CD=AD= ,∠D=90°,AB=5.BC=3.
(1)、在这次调查中D类型有多少名学生?(并在图中画出)(2)、写出被调查学生每人植树量的众数、中位数;(3)、求被调查学生每人植树量的平均数,并估计这260名学生共植树多少棵?20. 如图,在四边形ABCD中,CD=AD= ,∠D=90°,AB=5.BC=3. (1)、求∠C的度数;(2)、求四边形ABCD的面积.21. 阅读下列一段文字,然后回答下列问题.
(1)、求∠C的度数;(2)、求四边形ABCD的面积.21. 阅读下列一段文字,然后回答下列问题.已知平面内两点 M(x1,y1)、N(x2,y2),则这两点间的距离可用下列公式计算: MN= .
例如:已知 P(3,1)、Q(1,﹣2),则这两点间的距离 PQ= = .
特别地,如果两点 M(x1,y1)、N(x2,y2)所在的直线与坐标轴重合或平行于坐标轴或垂直于坐 标轴,那么这两点间的距离公式可简化为 MN=丨 x1﹣x2 丨或丨 y1﹣y2 丨.
(1)、已知 A(1,2)、B(﹣2,﹣3),试求 A、B 两点间的距离;(2)、已知 A、B 在平行于 x 轴的同一条直线上,点 A 的横坐标为 5,点 B 的横坐标为﹣1,试求 A、B 两 点间的距离;
(3)、已知△ABC 的顶点坐标分别为 A(0,4)、B(﹣1,2)、C(4,2),你能判定△ABC 的形状 吗?请说明理由.22. 如图,∠ADE+∠BCF=180°,BE平分∠ABC,∠ABC=2∠E.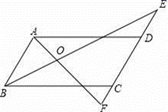 (1)、AD与BC平行吗?请说明理由;(2)、AB与EF的位置关系如何?为什么?(3)、若AF平分∠BAD,试说明:∠E+∠F=90°23. 如图,直线l:y=﹣ x+2与x轴,y轴分别交于A,B两点,在y轴上有一点C(0,4),动点M从点A出发以每秒1个单位的速度沿x轴向左移动.
(1)、AD与BC平行吗?请说明理由;(2)、AB与EF的位置关系如何?为什么?(3)、若AF平分∠BAD,试说明:∠E+∠F=90°23. 如图,直线l:y=﹣ x+2与x轴,y轴分别交于A,B两点,在y轴上有一点C(0,4),动点M从点A出发以每秒1个单位的速度沿x轴向左移动. (1)、求A,B两点的坐标;(2)、求△COM的面积S与点M的移动时间t之间的函数关系式;(3)、当t=6时,
(1)、求A,B两点的坐标;(2)、求△COM的面积S与点M的移动时间t之间的函数关系式;(3)、当t=6时,①直接写出直线CM所对应的函数表达式;
②问直线CM与直线 有怎样的位置关系?请说明理由.