江西省吉安市吉安县2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-04-01 类型：期末考试

进入出卷网下载

一、单选题

1. 在-1.4141， $\sqrt{2}$ ， $π$ ， $2 + \sqrt{3}$ ， $\sqrt{4}$ ，3.14这些数中，无理数的个数为（）

A、2 B、3 C、4 D、5

查看试题解析
2. 下列方程组中，是二元一次方程组的是（）

A、 ${\begin{array}{l} x + 2 y = 6 \\ 2 y - 3 z = 5 \end{array}$ B、 ${\begin{array}{l} x + \frac{1}{y} = 2 \\ 2 x - y = 1 \end{array}$ C、 ${\begin{array}{l} x + y = 4 \\ 2 x - y = 5 \end{array}$ D、 ${\begin{array}{l} x + y = 4 \\ x y = 3 \end{array}$

查看试题解析
3. 点 $P (- 3, 2)$ 关于 $x$ 轴的对称点的坐标是（）

A、 $(3, 2)$ B、 $(- 3, 2)$ C、 $(3, - 2)$ D、 $(- 3, - 2)$

查看试题解析
4. 下列各组数，能够作为直角三角形的三边长的是（）

A、4，6，8 B、 $\sqrt{3}$ ， $\sqrt{4}$ ， $\sqrt{5}$ C、5，12，14 D、 $2 \sqrt{3}$ ， $2 \sqrt{2}$ ， $2 \sqrt{5}$

查看试题解析
5. 下列四个命题中，假命题有（）
⑴两条直线被第三条直线所截，内错角相等．（2）如果 $∠ 1$ 和 $∠ 2$ 是对顶角，那么 $∠ 1 = ∠ 2$ ．（3）一个锐角的余角一定小于这个锐角的补角．（4）如果 $∠ 1$ 和 $∠ 3$ 互余， $∠ 2$ 与 $∠ 3$ 的余角互补，那么 $∠ 1$ 和 $∠ 2$ 互补．

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 古诗词比赛中，王二根据七位评委给某位参赛选手的分数制作了如下表格：

众数

中位数

平均数

方差

8.5

8.3

8.1

0.15

如果去掉一个最高分和一个最低分，那么表格中数据一定不发生变化的是（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
7. 菱形的一个内角是 $60 °$ ，边长是 $3 cm$ ，则这个菱形的较短的对角线长是（）

A、 $\frac{3}{2} cm$ B、 $\frac{3}{2} \sqrt{3} cm$ C、 $3 cm$ D、 $3 \sqrt{3} cm$

查看试题解析
8. 如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长是 $a$ ，则图中四个小正方形 $A 、 B 、 C 、 D$ 的面积之和是（）

A、 $a^{2}$ B、 $\frac{1}{2} a^{2}$ C、 $2 a^{2}$ D、不能确定

查看试题解析
9. 如图①，在矩形 $A B C D$ 中，动点P从点B出发，沿 $B C$ 、 $C D$ 、 $D A$ 运动至点A停止，设点P运动的路程为x， $Δ A B P$ 的面积为y，如果y关于x的函数图象如图②所示，则 $Δ A B C$ 的面积是（）

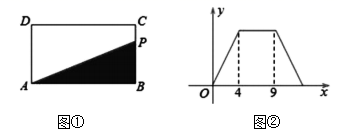A、10 B、16 C、18 D、20

查看试题解析
10. 一次函数y=ax+b的图象如图所示，则代数式∣a-b∣+∣a+b∣化简后的结果为（）.

A、-2a B、2a C、-2b D、2b

查看试题解析

二、填空题

11. 若 ${(a - 2)}^{2} + \sqrt{b + 3} = 0$ ，则 $a + b$ 的值是．

查看试题解析
12. 已知三角形三边长分别为 $\sqrt{6}$ ， $\sqrt{6}$ ， $2 \sqrt{3}$ ，则此三角形最大边上的高为．

查看试题解析
13. 在平面直角坐标系中，将点 $P (- 1, 2)$ 向下平移2个单位长度，再向左平移1个单位长度得到点 $Q$ ，则点 $Q$ 的坐标为．

查看试题解析
14. 一副透明的三角板，如图叠放，直角三角板的斜边AB、CE相交于点D，则∠BDC＝．

查看试题解析
15. 如图，将Rt△ABC放置在平面直角坐标系中，C与原点重合，CB在x轴上，若AB=2，点B的坐标为（4，0），则点A的坐标为.

查看试题解析
16. 如图，在直角坐标系中，点 $A$ 、 $B$ 的坐标分别为 $(1 ， 3)$ 和 $(4 ， 0)$ ，点 $C$ 是 $y$ 轴上的一个动点，当 $| B C - A C |$ 最大时，点 $C$ 的坐标是．

查看试题解析

三、解答题

17. 计算： $\sqrt{27} + {(- 1)}^{3} - 6 \times \frac{\sqrt{3}}{3}$

查看试题解析
18. 解方程组 ${\begin{array}{l} \frac{x + 2 y}{2} - x = 2 \\ x + 2 y = 4 \end{array}$

查看试题解析
19. 在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形） $A B C$ 的顶点 $A$ ， $B$ ， $C$ 的坐标分别为 $(- 3 ， 3)$ ， $(- 1 ， - 1)$ ， $(0 ， 1)$ ．

(1)、请在如图所示的网格平面内作出平面直角坐标系；

(2)、请作出 $△ A B C$ 关于 $x$ 轴对称的 $△ A^{'} B^{'} C^{'}$ ；

(3)、写出点 $B$ 的对应点B′的坐标．

查看试题解析
20. 如图，已知一次函数 $y = k x + b$ 的图象经过A （－2，－1）， B （1，3）两点，并且交x轴于点C，交y轴于点D．

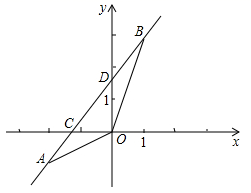(1)、求该一次函数的解析式

(2)、△AOB的面积

查看试题解析

21. 某中学八年级的篮球队有10名队员

.

在“二分球”罚篮投球训练中，这10名员各投篮50次的进球情况如下表：

进球数	42	32	26	20	19	18
人数	1	1	2	1	2	3

$[$ 投篮命中率 $= ($ 进球数 $\div$ 投篮次数 $) \times 100 %]$

针对这次训练，请解答下列问题：

(1)、求这10名队员进球数的平均数、中位数；

(2)、求这支球队投篮命中率；

(3)、若队员小亮“二分球”的投篮命中率为

55 %

，请你分析一下小亮在这支球队中的投篮水平．

查看试题解析

22. 如图所示，已知 $P$ 为正方形 $A B C D$ 外的一点． $P A = 1$ ， $P B = 2$ ．将 $△ A B P$ 绕点 $B$ 顺时针旋转 $90 °$ ，使点 $P$ 旋转至点 $P^{'}$ ，且 $A P^{'} = 3$ ，求 $∠ B P^{'} C$ 的度数．

查看试题解析
23. 某市蔬菜基地有一批蔬菜若干吨，有三种销售方式，利润如下表

销售方式

市场直接销售

粗加工销售

精加工销售

每吨获利（万元）

0.1

0.45

0.75

已知加工能力如下：若蔬菜总量再增加20吨，粗加工刚好10天全部加工完.若蔬菜总量减少20吨，精加工刚好20天全部加工完，且精加工比粗加工每天少加工10吨，又精加工和粗加工不能同时进行，而受季节限制，基地必须要15天（含15天）内全部加工或销售，为此基地特制定了三种方案：①尽可能多的精加工，来不及加工的在市场上直接销售，②全部粗加工，③将一部分精加工，其余蔬菜粗加工，且刚好15天完成.

解答下列问题：

(1)、求基地这批蔬菜有多少吨？

(2)、哪种方案获利最多？最多为多少万元？

查看试题解析
24. 如图，在平面直角坐标系中， $O$ 为坐标原点，点 $A$ 的坐标为 $(4 ， 0)$ ，点 $B$ 的坐标为 $(0 ， b) (b > 0)$ ，点 $P$ 是直线 $A B$ 上位于第二象限内的一个动点，过点 $P$ 作 $P C ⊥ x$ 轴于点 $C$ ，记点 $P$ 关于 $y$ 轴的对称点为 $Q$ ．设点 $P$ 的横坐标为 $a$ ．

(1)、当 $b = 3$ 时，
①求直线 $A B$ 的表达式；

②若 $Q O = Q A$ ，求点 $P$ 的坐标；

(2)、是否同时存在 $a$ ， $b$ ，使得 $△ Q A C$ 是等腰直角三角形？若存在，求出所有满足条件的 $a$ ， $b$ 的值；若不存在，请说明理由．

查看试题解析

销售方式	市场直接销售	粗加工销售	精加工销售
每吨获利（万元）	0.1	0.45	0.75

众数	中位数	平均数	方差
8.5	8.3	8.1	0.15