江西省赣州市于都县2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-04-01 类型：期末考试

进入出卷网下载

一、单选题

1. 下列电动车品牌标志中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 2019年被称为“5G元年”．据媒体报道，5G网络的理论下载速度为1.25GB/s，这就意味着我们下载一张2.5M的照片只需要0.002s，将0.002用科学记数法表示为（）

A、 $2 \times 10^{- 2}$ B、 $2 \times 10^{- 3}$ C、 $0.2 \times 10^{- 2}$ D、 $0.2 \times 10^{- 3}$

查看试题解析
3. 下列运算结果为 $a^{6}$ 的是（）

A、 ${(a^{6} + 1)}^{0} - 1$ B、 $a^{3} \cdot a^{2}$ C、 ${(a^{2})}^{3}$ D、 $a^{18} \div a^{3}$

查看试题解析
4. 已知△ABC ，两个完全一样的三角板如图摆放，它们的一组对应直角边分别在AB ， AC上，且这组对应边所对的顶点重合于点M ，点M一定在（）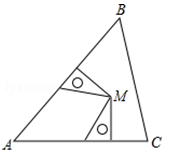

A、∠A的平分线上 B、AC边的高上 C、BC边的垂直平分线上 D、AB边的中线上

查看试题解析
5. 如图，在 $△ A B C$ 中， $A B = A C$ ，过点 $A$ 作 $D A ⊥ A C$ 交 $B C$ 于点 $D$ .若 $∠ B = 2 ∠ B A D$ ，则 $∠ B A D$ 的度数为（）

A、18° B、20° C、30° D、36°

查看试题解析
6. 我市防汛办为解决台风季排涝问题，准备在一定时间内铺设一条长4000米的排水管道，实际施工时， .求原计划每天铺设管道多少米？题目中部分条件被墨汁污染，小明查看了参考答案为：“设原计划每天铺设管道x米，则可得方程 $\frac{4000}{x - 10} - \frac{4000}{x}$ ＝20，…”根据答案，题中被墨汁污染条件应补为（）

A、每天比原计划多铺设10米，结果延期20天完成 B、每天比原计划少铺设10米，结果延期20天完成 C、每天比原计划多铺设10米，结果提前20天完成 D、每天比原计划少铺设10米，结果提前20天完成

查看试题解析

二、填空题

7. 若分式 $\frac{x + 1}{x - 1}$ 有意义，x 的取值范围是.

查看试题解析
8. 如图， $△ A B C ≅ △ A D E$ ，如果 $A B = 5 c m ， B C = 7 c m ， A C = 6 c m$ ，那么 $D E$ 的长是.

查看试题解析
9. 学习了“分式的加法”的相关知识后，小明同学画出了如图：请问他画的图中①为， ②为．

查看试题解析
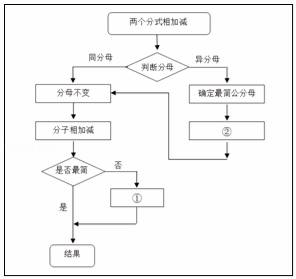10. 在 $△ A B C$ 中，已知 $A B = 3$ ， $B C = a$ ， $a$ 的取值范围在数轴上表示如图所示，则 $A C$ 的长为

查看试题解析
11. 生活中，有人喜欢把传送的便条折成形状，折叠过程如图所示（阴影部分表示纸条的反面）：

已知由信纸折成的长方形纸条（图①）长为 $25 cm$ ，宽为 $x cm$ .如果能折成图④的形状，且为了美观，纸条两端超出点 $P$ 的长度相等，即最终图形是轴对称图形，则在开始折叠时起点 $M$ 与点 $A$ 的距离（用 $x$ 表示）为 $cm$ ．

查看试题解析
12. 我们知道，假分数可以化为整数与真分数的和的形式，例如： $\frac{3}{2} = 1 + \frac{1}{2}$ ，在分式中，对于只含有一个字母的分式，当分子的次数大于或等于分母的次数时，我们称之为“假分式”；如果假分式 $\frac{x^{2} + 4 x + 1}{x + 2}$ 的值为整数，则 $x$ 的负整数值为．

查看试题解析
13. 下面是“求作∠AOB的角平分线”的尺规作图过程．
已知：如图，钝角∠AOB．

求作：∠AOB的角平分线．

作法：

①在OA和OB上，分别截取OD、OE，使OD=OE；

②分别以D、E为圆心，大于 $\frac{1}{2}$ DE的长为半径作弧，在∠AOB内，两弧交于点C；

③作射线OC．

所以射线OC就是所求作的∠AOB的角平分线．

请回答：该尺规作图的依据是．

查看试题解析

三、解答题

14. 计算：

(1)、化简： $(x - y) (x + 3 y) - x (x + 2 y)$

(2)、如图， $∠ A B E$ 是四边形 $A B C D$ 的一个外角，且 $∠ A B E = ∠ D$ ，那么 $∠ A$ 与 $∠ C$ 互补吗？为什么？

查看试题解析
15. 已知点 $A (2 a - b ， 5 + a)$ ， $B (2 b - 1 ， - a + b)$ .若 $A$ 、 $B$ 关于 $y$ 轴对称，求 ${(4 a + b)}^{2020}$ 的值．

查看试题解析
16. 先化简，再求值： $(1 - \frac{2 a - 1}{a^{2}}) \div \frac{a^{2} - 1}{a^{2} + a}$ ，其中 $a = {(\frac{1}{2})}^{- 1}$

查看试题解析
17. 如图，六个完全相同的小长方形拼成了一个大长方形， $A$ 、 $B$ 是如图所示小长方形的顶点，请在大长方形中按下列要求完成画图：

(1)、请你仅用无刻度直尺在图1中画一个等腰 $Rt △ A B C$ ，其中 $∠ A B C = 90 °$ ；

(2)、请你仅用无刻度直尺在图2作出线段 $A B$ 的垂直平分线．

查看试题解析
18. 如图，已知在等腰三角形ABC中，AB＝AC，∠BAC＝80°，AD⊥BC，AD＝AB，联结BD并延长，交AC的延长线于点E，求∠E的度数．

查看试题解析
19. 新冠肺炎疫情防控期间，学校为做好预防性消毒工作，开学初购进 $A$ 、 $B$ 两种消毒液，其中 $A$ 消毒液的单价比 $B$ 消毒液的单价多40元，用3200元购买 $B$ 消毒液的数量是用2400元购买 $A$ 消毒液数量的2倍．

(1)、求两种消毒液的单价；

(2)、学校准备用不多于6800元的资金购买 $A$ 、 $B$ 两种消毒液共70桶，问最多购买 $A$ 消毒液多少桶？

查看试题解析
20. 如图，已知 $△ A B C$ 与 $△ A D G$ 均为等边三角形，点 $E$ 在 $G D$ 的延长线上，且 $G E = A C$ ，连接 $A E$ 、 $B D$ ．

(1)、求证： $△ A G E ≌ △ D A B$ ；

(2)、 $F$ 是 $B C$ 上的一点，连接 $A F$ 、 $E F$ ， $A F$ 与 $G E$ 相交于 $M$ ，若 $△ A E F$ 是等边三角形，求证： $B D // E F$ ．

查看试题解析
21. 将边长为a的正方形的左上角剪掉一个边长为b的正方形（如图1），将剩下部分按照虚线分割成①和②两部分，将①和②两部分拼成一个长方形（如图2）．

(1)、设图1中阴影部分的面积为S₁，图2中阴影部分的面积为S₂，请用含a．b的式子表示：S₁＝， S₂＝；（不必化简）

(2)、以上结果可以验证的乘法公式是．

(3)、利用（2）中得到的公式，计算；2020²﹣2019×2021．

查看试题解析
22. 如图， $O$ 为 $△ A B C$ 内部一点， $P$ 、 $R$ 分别为点 $O$ 关于直线 $A B$ 、 $B C$ 对称的点．

(1)、若 $∠ A B C = 60 °$ ，求 $∠ P O R$ 的度数；

(2)、试猜想当 $P R$ 的值最大时， $∠ A$ 与 $∠ C$ 需要满足什么数量关系，并说明理由．

查看试题解析
23. 某数学兴趣小组开展了一次活动，过程如下：
设 $∠ B A C = θ (0 ° < θ < 90 °)$ ，小棒依次摆放在两射线之间，并使小棒两端分别落在两射线上．

(1)、活动一：
如图甲所示，从点 $A_{1}$ 开始，依次向右摆放小棒，使小棒与小棒在端点处互相垂直， $A_{1} A_{2}$ 为第1根小棒．

数学思考：

小棒能无限摆下去吗？答：；（填“能”或“不能”）

(2)、若 $A A_{1} = A_{1} A_{2} = A_{2} A_{3} = 1$ ，则 $θ =$ 度；

(3)、活动二：
如图乙所示，从点 $A_{1}$ 开始，用等长的小棒依次向右摆放，其中 $A_{1} A_{2}$ 为第1根小棒，且 $A_{1} A_{2} = A A_{1}$ ．

数学思考：

若已经向右摆放了3根小棒，则 $θ_{1} =$ ， $θ_{2} =$ ， $θ_{3} =$ （用含 $θ$ 的式子表示）；

(4)、若只能摆放4根小棒，求 $θ$ 的范围．

查看试题解析