江西省赣州市2020-2021学年八年级上学期数学期末试卷
试卷更新日期:2021-04-01 类型:期末考试
一、单选题
-
1. 自新冠肺炎疫情发生以来,全国人民共同抗疫,各地积极普及科学防控知识.下面是科学防控知识的图片,图片上有图案和文字说明,其中的图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 以下列各线段长为边,能组成三角形的是( )A、 B、 C、 D、3. 在 中, , 平分 ,交 于点D, ,垂足为点E,若 ,则 的长为( )
2. 以下列各线段长为边,能组成三角形的是( )A、 B、 C、 D、3. 在 中, , 平分 ,交 于点D, ,垂足为点E,若 ,则 的长为( ) A、3 B、 C、2 D、64. 在联欢会上,有 、 、 三名选手站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在 的( )A、三边中线的交点 B、三条角平分线的交点 C、三边中垂线的交点 D、三边上高所在直线的交点5. 如图,在 中, , , 是 上一点,将 沿 折叠,使点 落在 边上的 处,则 等于( )
A、3 B、 C、2 D、64. 在联欢会上,有 、 、 三名选手站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在 的( )A、三边中线的交点 B、三条角平分线的交点 C、三边中垂线的交点 D、三边上高所在直线的交点5. 如图,在 中, , , 是 上一点,将 沿 折叠,使点 落在 边上的 处,则 等于( ) A、25° B、30° C、40° D、55°6. 如图, AD是 的中线,E、F分别是AD和AD延长线上的点,且 ,连结BF、CE . 下列说法:①CE=BF②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有( )
A、25° B、30° C、40° D、55°6. 如图, AD是 的中线,E、F分别是AD和AD延长线上的点,且 ,连结BF、CE . 下列说法:①CE=BF②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有( )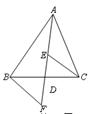 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
7. 在平面直角坐标系中,将点P(﹣3,2)向右平移3个单位得到点 ,则点 关于x轴的对称点的坐标为 .8. 如图,已知在△ABD和△ABC中,∠DAB=∠CAB , 点A、B、E在同一条直线上,若使△ABD≌△ABC , 则还需添加的一个条件是 . (只填一个即可)
 9. 如图,在 中, 是 的垂直平分线.若 , 的周长为13,则 的周长为.
9. 如图,在 中, 是 的垂直平分线.若 , 的周长为13,则 的周长为.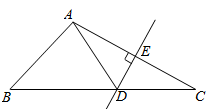 10. 如图,把 放置在平面直角坐标系中,已知 , , , ,点 在第四象限,则点 的坐标是 .
10. 如图,把 放置在平面直角坐标系中,已知 , , , ,点 在第四象限,则点 的坐标是 . 11. 如图,在 中, , , 面积为12, 于点 ,直线 垂直平分 交 于点 ,交 于点 , 为直线 上一动点,则 周长的最小值为 .
11. 如图,在 中, , , 面积为12, 于点 ,直线 垂直平分 交 于点 ,交 于点 , 为直线 上一动点,则 周长的最小值为 . 12. 当三角形中一个内角 是另一个内角 的2倍时,则称此三角形为“倍角三角形”,其中角 称为“倍角”.若“倍角三角形”中有一个内角为36°,则这个“倍角三角形”的“倍角”的度数可以是.
12. 当三角形中一个内角 是另一个内角 的2倍时,则称此三角形为“倍角三角形”,其中角 称为“倍角”.若“倍角三角形”中有一个内角为36°,则这个“倍角三角形”的“倍角”的度数可以是.三、解答题
-
13. 一个多边形,它的内角和比外角和的 倍多 求这个多边形的边数.14. 如图, 是 的平分线,点 是线段 上的一点, , .

求证: .
15. 请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹. (1)、如图①,四边形ABCD中,AB=AD, B= D,画出四边形ABCD的对称轴m;(2)、如图②,四边形ABCD中,AD∥BC, A= D,画出边BC的垂直平分线n.16. 三顶点 、 、 , 与 关于 轴对称.
(1)、如图①,四边形ABCD中,AB=AD, B= D,画出四边形ABCD的对称轴m;(2)、如图②,四边形ABCD中,AD∥BC, A= D,画出边BC的垂直平分线n.16. 三顶点 、 、 , 与 关于 轴对称. (1)、画出 ;(2)、求 的面积.17. 如图,在△ABC中,AB=AC,∠C=2∠A,BD是AC边上的高,求∠A和∠DBC的度数.
(1)、画出 ;(2)、求 的面积.17. 如图,在△ABC中,AB=AC,∠C=2∠A,BD是AC边上的高,求∠A和∠DBC的度数. 18. 如图,在 中, ,点 、 、 分别在 、 、 边上,且 , .
18. 如图,在 中, ,点 、 、 分别在 、 、 边上,且 , . (1)、求证: 为等腰三角形;(2)、当 时,求 的度数.19. 如图,在 中, , , 的外角 的平分线 交 的延长线于点 .
(1)、求证: 为等腰三角形;(2)、当 时,求 的度数.19. 如图,在 中, , , 的外角 的平分线 交 的延长线于点 . (1)、求 的度数;(2)、点 是 延长线上一点,过点 作 ,交 的延长线于点 .求证: .20. 如图,在等边三角形 中,点 , 分别在边 , 上,且 ,过点 作 ,交 的延长线于点 .
(1)、求 的度数;(2)、点 是 延长线上一点,过点 作 ,交 的延长线于点 .求证: .20. 如图,在等边三角形 中,点 , 分别在边 , 上,且 ,过点 作 ,交 的延长线于点 . (1)、求证: ;(2)、若 ,求 的长.21. 已知: , , , .
(1)、求证: ;(2)、若 ,求 的长.21. 已知: , , , . (1)、试猜想线段 与 的位置关系,并证明你的结论.(2)、若将 沿 方向平移至图2情形,其余条件不变,结论 还成立吗?请说明理由.(3)、若将 沿 方向平移至图3情形,其余条件不变,结论 还成立吗?请说明理由.22. 直线 与直线 垂直相交于 ,点 在直线 上运动,点 在直线 上运动.
(1)、试猜想线段 与 的位置关系,并证明你的结论.(2)、若将 沿 方向平移至图2情形,其余条件不变,结论 还成立吗?请说明理由.(3)、若将 沿 方向平移至图3情形,其余条件不变,结论 还成立吗?请说明理由.22. 直线 与直线 垂直相交于 ,点 在直线 上运动,点 在直线 上运动. (1)、如图1,已知 、 分别是 和 的角平分线,点 , 在运动的过程中, 的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出 的大小.
(1)、如图1,已知 、 分别是 和 的角平分线,点 , 在运动的过程中, 的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出 的大小. (2)、如图2,已知 不平行 , 、 分别是 和 的角平分线, 、 分别是 和 的角平分线,点 、 在运动的过程中, 的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.23. (问题背景)
(2)、如图2,已知 不平行 , 、 分别是 和 的角平分线, 、 分别是 和 的角平分线,点 、 在运动的过程中, 的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.23. (问题背景)在四边形 中, , , , 、 分别是 、 上的点,且 ,试探究图1中线段 、 、 之间的数量关系.

(初步探索)
小晨同学认为:延长 到点 ,使 ,连接 ,先证明 ,再证明 ,则可得到 、 、 之间的数量关系是.
(探索延伸)
在四边形 中如图2, , , 、 分别是 、 上的点, ,上述结论是否仍然成立?说明理由.
(结论运用)
如图3,在某次南海海域军事演习中,舰艇甲在指挥中心( 处)北偏西30°的 处,舰艇乙在指挥中心南偏东70°的 处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以80海里/小时的速度前进,舰艇乙沿北偏东50°的方向以100海里/小时的速度前进1.2小时后,指挥中心观测到甲、乙两舰艇分别到达 , 处,且两舰艇之间的夹角( )为70°,试求此时两舰艇之间的距离.