初中数学湘教版八年级下学期期中复习专题1 直角三角形的性质
试卷更新日期：2021-04-01 类型：复习试卷
一、单选题
-
1. 满足下列条件的三角形中，不是直角三角形的是（ ）A、∠A-∠B=∠C B、∠A：∠B：∠C=3：4：7 C、∠A=2∠B=3∠C D、∠A=9°，∠B=81°2. 如果一个三角形的三条高的交点恰是三角形的一个顶点，那么这个三角形是（ ）A、锐角三角形 B、钝角三角形 C、直角三角形 D、都有可能3. 如图由于台风的影响，一棵树在离地面 处折断，折断后树干上部分与地面成30度的夹角，折断前长度是 （ ）
A、 B、 C、 D、 .4. 如右图是屋架设计图的一部分，点D是斜梁AB的中点，立柱BC、DE垂直于横梁AC，AB=7.4m，∠A=30°，DE的长为（ ）
A、7.4m B、3.7m C、1.85m D、2.85m5. 将一根长24cm的筷子置于底面直径为5cm，高为12cm的圆柱水杯中，设筷子露在杯子外面的长度为h，则h的取值范围是（ ）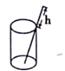
A、12cm≤h≤19cm B、12cm≤h≤13cm C、11cm≤h≤12cm D、5cm≤h≤12cm6. 如图是2002年8月在北京召开的国际数学家大会的会标，它取材于我国古代数学家赵爽的《勾股圆方图》，由四个全等的直角三角形和一个小正方形的拼成的大正方形，如果大正方形的面积是5，小正方形的面积是1，直角三角形的较短边为a，较长边为b，那么（a+b）2的值是（ ）
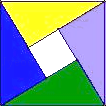A、4 B、9 C、16 D、257. 若一个三角形三边满足（a+b）2﹣c2=2ab，则这个三角形是（ ）
A、直角三角形 B、等腰直角三角形 C、等腰三角形 D、以上结论都不对8. 下列各组数中，是勾股数的是（ ）A、0.3，0.4，0.5 B、 ， ， C、6，8，10 D、1.5，2，2.59. 我国古代数学家赵爽的弦图，它是由四个全等的直角三角形和中间的小正方形拼成的大正方形，如图所示，如果大正方形的面积是13，小正方形的面积为1，直角三角形的较短直角边长为a ， 较长直角边长为b ， 那么(a＋b)2的值为( )
A、13 B、19 C、25 D、16910. 如图，AD⊥CD，CD=4，AD=3，∠ACB=90°，AB=13，则 BC 的长是（ ）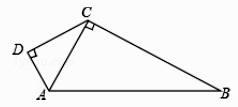
A、8 B、10 C、12 D、1611. 已知Rt△ABC中，∠C=90°，若a+b=10cm，c=8cm，则Rt△ABC的面积为（ ）A、9cm2 B、18cm2 C、24cm² D、36cm212. 将一根长为25厘米的筷子至于底面直径为5厘米，高为12厘米的圆柱形水杯中，设筷子漏在杯子外的长为h厘米，则h的取值范围是（ ）A、12≤h≤13 B、11≤h≤12 C、11≤h≤13 D、10≤h≤12二、填空题
-
13. 在Rt
ABC中，∠C=90°，∠A=65°，则∠B=. 14. 如图，Rt△ABC中，∠ACB=90°，D为斜边AB的中点，AB=6cm，则CD的长为cm.
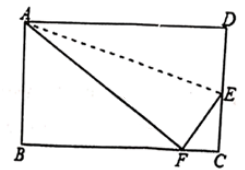
15. 如图，在Rt△ABC中，∠ACB=90°，∠A=30°，CD是斜边AB上的高，若AB=8，则BD= ．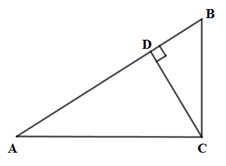
16. 如图，在四边形ABCD中，∠B=∠D=90°，∠A=60°，AB=4，则AD的取值范围是 ．
17. 如图，作一个长方形，以数轴的原点为中心，长方形对角线为半径，交数轴于点A，则点A表示的数是 ．
18. 如图，将长AB=5cm，宽AD=3cm的矩形纸片ABCD折叠，使点A与C重合，折痕为EF，则AE长为cm．
三、计算题
-
19. 在 Rt△ABC 中，∠C＝90°，∠A、∠B、∠C 的对边分别为 a、b、c ． 若 a∶c＝15∶17，b＝24，求 a.
四、解答题
-
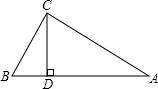
20. 如图， 中， ，CD是 的高， ， ，求BD长．
21. 如图 ，小明在A处看见前面山上有个气象站，测得仰角为15°（即∠CAB=15°），当笔直向山行6千米时，小明看气象站测得仰角为30°（即∠CBD=30°）.你能算处这个气象站离地面的高度CD吗？是多少?
22. 如图，在Rt△ABC中，∠ACB=90°，D是AB上一点，且∠ACD=∠B，求证：CD⊥AB．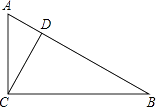
23. 如图∠B=∠ACD=90°， AD=13，CD=12， BC=3，则AB的长是多少?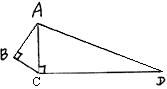
五、综合题
-
