初中数学苏科版九年级下册7.5 解直角三角形 同步训练
试卷更新日期:2021-04-01 类型:同步测试
一、单选题
-
1. 关于直角三角形,下列说法正确的是( )A、所有的直角三角形一定相似 B、如果直角三角形的两边长分别是3和4,那么第三边的长一定是5 C、如果已知直角三角形两个元素(直角除外),那么这个直角三角形一定可解 D、如果已知直角三角形一锐角的三角函数值,那么这个直角三角形的三边之比一定确定2. 如图,为测量河两岸相对两电线杆 、 间的距离,在距 点 的 处 ,测得 ,则 、 之间的距离应为( )
 A、16sin52° m B、16cos52° m C、16tan52° m D、 m3. 如图,AC是旗杆AB的一根拉线,拉直AC时,测得BC=3米,∠ACB=50°,则AB的高为( )
A、16sin52° m B、16cos52° m C、16tan52° m D、 m3. 如图,AC是旗杆AB的一根拉线,拉直AC时,测得BC=3米,∠ACB=50°,则AB的高为( )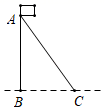 A、3cos50°米 B、3tan50°米 C、 米 D、 米4. 在 中, , ,若 ,则AB的长为( )A、 B、 C、 D、5. 如图,某游乐场一山顶滑梯的高为h,滑梯的坡角为a,那么滑梯长l为( )
A、3cos50°米 B、3tan50°米 C、 米 D、 米4. 在 中, , ,若 ,则AB的长为( )A、 B、 C、 D、5. 如图,某游乐场一山顶滑梯的高为h,滑梯的坡角为a,那么滑梯长l为( )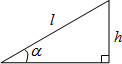 A、 B、 C、 D、6. 有一副三角板,含45°的三角板的斜边与含30°的三角板的长直角边相等,如图,将这副三角板直角顶点重合拼放在一起,点B,C,E在同一直线上,若BC=2,则AF的长为( )
A、 B、 C、 D、6. 有一副三角板,含45°的三角板的斜边与含30°的三角板的长直角边相等,如图,将这副三角板直角顶点重合拼放在一起,点B,C,E在同一直线上,若BC=2,则AF的长为( )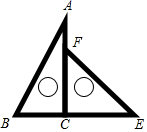 A、2 B、2 ﹣2 C、4﹣2 D、2 ﹣7. 如图,在△ABC中,∠C=90°,AC=5,若cosA= ,则BC的长为( )
A、2 B、2 ﹣2 C、4﹣2 D、2 ﹣7. 如图,在△ABC中,∠C=90°,AC=5,若cosA= ,则BC的长为( )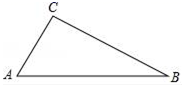 A、8 B、12 C、13 D、188. 西周时期,丞相周公旦设置过一种通过测定日影长度来确定时间的仪器,称为圭表.如图是一个根据北京的地理位置设计的圭表,其中,立柱AC高为a.已知,冬至时北京的正午日光入射角∠ABC约为26.5°,则立柱根部与圭表的冬至线的距离(即BC的长)约为( )
A、8 B、12 C、13 D、188. 西周时期,丞相周公旦设置过一种通过测定日影长度来确定时间的仪器,称为圭表.如图是一个根据北京的地理位置设计的圭表,其中,立柱AC高为a.已知,冬至时北京的正午日光入射角∠ABC约为26.5°,则立柱根部与圭表的冬至线的距离(即BC的长)约为( ) A、asin26.5° B、 C、acos26.5° D、9. 如图,在 中, , , ,若 是 边上的动点,则 的最小值( )
A、asin26.5° B、 C、acos26.5° D、9. 如图,在 中, , , ,若 是 边上的动点,则 的最小值( )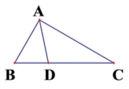 A、 B、6 C、 D、410. 如图,将矩形ABCD绕点A旋转至矩形AEFG的位置,此时点D恰好与AF的中点重合,AE交CD于点H,若BC=2 ,则HC的长为( )
A、 B、6 C、 D、410. 如图,将矩形ABCD绕点A旋转至矩形AEFG的位置,此时点D恰好与AF的中点重合,AE交CD于点H,若BC=2 ,则HC的长为( )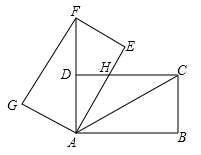 A、4 B、2 C、3 D、6
A、4 B、2 C、3 D、6二、填空题
-
11. 在Rt△ABC中,∠ C=90°,sinA= ,AC=24,则AB=.12. 在 中, ,则 的面积为.13. 如图,点 在线段 上, , , ,如果 , , ,那么 的长是 .
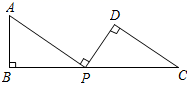 14. 如图,∠EFG=90°,EF=10,OG=17,cos∠FGO= ,则点F的坐标是.
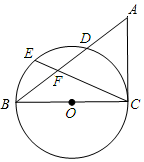
14. 如图,∠EFG=90°,EF=10,OG=17,cos∠FGO= ,则点F的坐标是. 15. 如图, △ABC内接于⊙O,AB=BC,∠ABC=120° ,AD为⊙O的直径,AD=6,那么BD=
15. 如图, △ABC内接于⊙O,AB=BC,∠ABC=120° ,AD为⊙O的直径,AD=6,那么BD= 16. 如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°,AC=6,现将Rt△ABC绕点A顺时针旋转30°得到△AB'C’,则图中阴影部分面积为 .
16. 如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°,AC=6,现将Rt△ABC绕点A顺时针旋转30°得到△AB'C’,则图中阴影部分面积为 .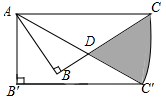 17. 新定义:有一组对角互余的凸四边形称为对余四边形.如图,已知在对余四边形 中, , , , ,那么边 的长为 .
17. 新定义:有一组对角互余的凸四边形称为对余四边形.如图,已知在对余四边形 中, , , , ,那么边 的长为 . 18. 如图,在菱形 中, , ,点P,Q,K分别为线段 , , 上的任意一点,则 的最小值为.
18. 如图,在菱形 中, , ,点P,Q,K分别为线段 , , 上的任意一点,则 的最小值为.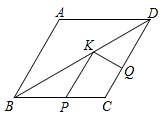
三、解答题
-
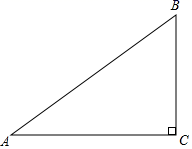
19. 如图,在Rt△ABC中,∠C=90˚,tanA ,BC=6,求AC的长和sinA的值.
 20. 如图,在Rt△ABC中,∠ACB=900 , CD⊥AB于D,tan∠ABC= ,且BC=9cm,求AC,AB及CD的长.
20. 如图,在Rt△ABC中,∠ACB=900 , CD⊥AB于D,tan∠ABC= ,且BC=9cm,求AC,AB及CD的长. 21. 如图,在Rt△ABC中,∠C=90°,sinA= ,D为AC上一点,∠BDC=45°,DC=6 cm,求AB、AD的长.
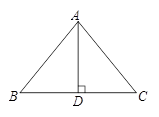
21. 如图,在Rt△ABC中,∠C=90°,sinA= ,D为AC上一点,∠BDC=45°,DC=6 cm,求AB、AD的长. 22. 我们把底角为51°的等腰三角形称为最稳定三角形. 如图,已知△ABC是最稳定三角形, AB=AC,BC=232.8m.求BC边上的高AD的长.
22. 我们把底角为51°的等腰三角形称为最稳定三角形. 如图,已知△ABC是最稳定三角形, AB=AC,BC=232.8m.求BC边上的高AD的长.(sin51°≈0.8,cos51°≈0.6,tan51°≈1.2,精确到1m)
 23. 如图,在 中, 是BC边上的高, , , .
23. 如图,在 中, 是BC边上的高, , , .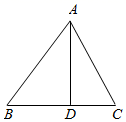 (1)、求线段 的长度:(2)、求 的值.24. 如图,已知∠MON=25°,矩形ABCD的边BC在OM上,对角线AC⊥ON.
(1)、求线段 的长度:(2)、求 的值.24. 如图,已知∠MON=25°,矩形ABCD的边BC在OM上,对角线AC⊥ON. (1)、求∠ACD度数;(2)、当AC=5时,求AD的长.(参考数据:sin25°=0.42;cos25°=0.91;tan25°=0.47,结果精确到0.1)
(1)、求∠ACD度数;(2)、当AC=5时,求AD的长.(参考数据:sin25°=0.42;cos25°=0.91;tan25°=0.47,结果精确到0.1)