初中数学苏科版九年级下册7.3 特殊角的三角函数同步训练

试卷更新日期：2021-04-01 类型：同步测试

进入出卷网下载

一、单选题

1. 计算：sin60°•tan30°＝（）

A、1 B、 $\frac{1}{2}$ C、 $\frac{\sqrt{3}}{2}$ D、2

查看试题解析
2. 下列各式中正确的是（）

A、 $\tan 45^{°} = \frac{\sqrt{2}}{2}$ B、 $\cos 45^{°} = 1$ C、 $\sin 30^{°} = \frac{1}{2}$ D、 $\tan 60^{°} = \frac{\sqrt{3}}{3}$

查看试题解析
3. 在Rt△ABC中，∠C=90°，AB=2BC，则cosA的值是（）

A、 $\frac{\sqrt{2}}{2}$ B、2 C、 $\frac{1}{2}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
4. Rt△ABC中，∠C=90°，sinA= $\frac{1}{2}$ ，则tanB的值是（）

A、 $\frac{\sqrt{3}}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{1}{2}$ D、 $\sqrt{3}$

查看试题解析
5. 若sin（75°-θ）的值是 $\frac{1}{2}$ ，则θ=（）

A、15° B、30° C、45° D、60°

查看试题解析
6. 点 $M (- \sin 30 °, \cos 30 °)$ 关于x轴对称的点的坐标是（）

A、 $(\frac{\sqrt{3}}{2}, \frac{1}{2})$ B、 $(- \frac{\sqrt{3}}{2}, - \frac{1}{2})$ C、 $(- \frac{\sqrt{3}}{2}, \frac{1}{2})$ D、 $(- \frac{1}{2}, - \frac{\sqrt{3}}{2})$

查看试题解析
7. 如图，每个小正方形的边长都为1，点A、B、C都在小正方形的顶点上，则∠ABC的正弦值为（）

A、1 B、 $\sqrt{3}$ C、 $\frac{1}{2}$ D、 $\frac{\sqrt{2}}{2}$

查看试题解析
8. 在△ABC中，若∠A、∠B满足|cosA﹣ $\frac{1}{2}$ |+（sinB﹣ $\frac{\sqrt{2}}{2}$ ）²=0，则∠C=（）

A、45° B、60° C、75° D、105°

查看试题解析
9. α为锐角，当 $\frac{1}{1 - \tan α}$ 无意义时，sin（α+15°）+cos（α﹣15°）的值为（）

A、 $\sqrt{3}$ B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{2 \sqrt{3}}{3}$

查看试题解析
10. 关于三角函数有如下公式：
sin（α+β）=sinαcosβ+cosαsinβ，sin（α﹣β）=sinαcosβ﹣cosαsinβ

cos（α+β）=cosαcosβ﹣sinαsinβ，cos（α﹣β）=cosαcosβ+sinαsinβ

tan（α+β）= $\frac{\tan α + \tan β}{1 - \tan α \tan β}$ （1﹣tanαtanβ≠0），合理利用这些公式可以将一些角的三角函数值转化为特殊角的三角函数来求值，如sin90°=sin（30°+60°）=sin30°cos60°+cos30°sin60°= $\frac{1}{2} \times \frac{1}{2} + \frac{\sqrt{3}}{2} \times \frac{\sqrt{3}}{2}$ =1

利用上述公式计算下列三角函数①sin105°= $\frac{\sqrt{6} + \sqrt{2}}{4}$ ，②tan105°=﹣2﹣ $\sqrt{3}$ ，③sin15°= $\frac{\sqrt{6} - \sqrt{2}}{4}$ ，④cos90°=0

其中正确的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 计算： $\cos 30^{\circ} \tan 45^{\circ} + \sin 60^{\circ} \tan 60^{\circ}$ =

查看试题解析
12. 在Rt△ABC中，∠C=90°，如果tan∠A= $\frac{\sqrt{3}}{3}$ ，那么cosB= ．

查看试题解析
13. 在 $△ A B C$ 中，∠A，∠B为锐角，sinA = $\frac{1}{2}$ ，tanB = $\frac{\sqrt{3}}{3}$ ，则 $△ A B C$ 的形状为

查看试题解析
14. 半径为3cm的⊙O中有长为 $3 \sqrt{3}$ 的弦AB，则弦AB所对的圆周角为

查看试题解析
15. 反比例函数 $y = \frac{k}{x}$ 的图象经过点（tan45°，cos60°），则k＝.

查看试题解析
16. 一般地，当a，β为任意角时，sin(a+β)与sin(a-β)的值可以用下面的公式求得：
sin(a+β)=sina·cosβ+cosa·sinβ:sin(a-β)=sina·cosβ-cosa·sinβ.例如sin90°=sin(60°+30°）=sin60°·cos30°+cos60°·sin30°= $\frac{\sqrt{3}}{2} \times \frac{\sqrt{3}}{2} + \frac{1}{2} \times \frac{1}{2}$ =1,类似地，可以求得sin15°的值是 .

查看试题解析
17. 已知⊙O的直径CD为4， $\overset{⌢}{A C}$ 的度数为80°，点B是 $\overset{⌢}{A C}$ 的中点，点P在直径CD上移动，则BP+AP的最小值为．

查看试题解析
18. 如图，平行四边形ABCD中，∠DAB=60°，AB=6，BC=2，P为边CD上的一动点，则 $P B + \frac{\sqrt{3}}{2} P D$ 的最小值等于.

查看试题解析

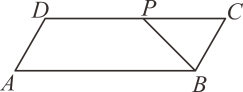
三、解答题

19. 计算：

(1)、 $2 \cos 30^{°} + 4 \sin 30^{°} - \tan 60^{°}$

(2)、 $2 \tan 60^{°} + \tan 45^{°} - 4 \cos 30^{°}$

(3)、 $3 \tan 30^{°} + \cos 45^{°} - 2 \sin 60^{°}$

查看试题解析
20. 先化简，再求代数式的值： $(\frac{2}{a + 1} + \frac{a + 2}{a^{2} - 1}) \div \frac{a}{a - 1}$ ，其中a=tan60°﹣2sin30°．

查看试题解析
21. 先化简，再求值： $\frac{a^{2}}{a^{2} + 2 a}$ ﹣ $\frac{a^{2} - 2 a + 1}{a + 2}$ ÷ $\frac{a^{2} - 1}{a + 1}$ ，其中a=cos30°﹣2tan45°．

查看试题解析
22. 先化简，再求代数式（ $\frac{1}{x + y}$ ﹣ $\frac{3}{x y + y^{2}}$ ）÷ $\frac{9 - 3 y}{y}$ 的值，其中x=2sin60°﹣1，y=tan45°．

查看试题解析
23. 先化简，再求代数式 $\frac{m^{2} - 2 m + 1}{m^{3} - m}$ ÷ $\frac{m - 1}{m}$ 的值，其中m=tan60°﹣2sin30°．

查看试题解析
24. 先化简，再求代数式 $\frac{a^{2} + 2 a}{a^{2} + 2 a + 1} \div (1 + \frac{1}{a + 1})$ 的值，其中a=tan60° $- \sqrt{2} \sin 45^{0}$ ．

查看试题解析
25. 先化简，再求代数式（ $\frac{2}{a + 1}$ ﹣ $\frac{2 a - 3}{a^{2} - 1}$ ）÷ $\frac{1}{a + 1}$ 的值，其中a=2sin60°+tan45°．

查看试题解析
26. 请先阅读这段内容.再解答问题
三角函数中常用公式 $\sin (α + β) = \sin α \cdot \cos β + \cos α \cdot \sin β$ .求 $\sin 75 °$ 的值，

即 $\sin 75 ° = \sin (30 ° + 45 °) = \sin 30 ° \cdot \cos 45 ° + \cos 30 ° \cdot \sin 45 ° = \frac{\sqrt{2} + \sqrt{6}}{4}$ .

试用公式 $\cos (α + β) = \cos α \cdot \sin β - \sin α \cdot \cos β$ ，求出 $\cos 75 °$ 的值.

查看试题解析
27. 小明在某次作业中得到如下结果：
sin²7°+sin²83°≈0.12²+0.99²=0.9945，
sin²22°+sin²68°≈0.37²+0.93²=1.0018，
sin²29°+sin²61°≈0.48²+0.87²=0.9873，
sin²37°+sin²53°≈0.60²+0.80²=1.0000，
sin²45°+sin²45°=（ $\frac{\sqrt{2}}{2}$ ）²+（ $\frac{\sqrt{2}}{2}$ ）²=1．
据此，小明猜想：对于任意锐角α，均有sin²α+sin²（90°﹣α）=1．
（Ⅰ）当α=30°时，验证sin²α+sin²（90°﹣α）=1是否成立；
（Ⅱ）小明的猜想是否成立？若成立，请给予证明；若不成立，请举出一个反例．

查看试题解析

初中数学苏科版九年级下册7.3 特殊角的三角函数 同步训练

一、单选题

二、填空题

三、解答题

初中数学苏科版九年级下册7.3 特殊角的三角函数同步训练