初中数学苏科版九年级下册7.2 正弦、余弦 同步训练
试卷更新日期:2021-04-01 类型:同步测试
一、单选题
-
1. 在ΔABC中,∠C=90º,AB=5,BC=3,则 的值是( )A、 B、 C、 D、2. 在 中, , ,那么 的值等于( )A、 B、 C、 D、3. 在 中, , ,若 ,则 的长为( ).A、 B、 C、 D、4. Rt△ABC中,如果各边长度都扩大 倍,则锐角A的各个三角函数值( )A、不变化 B、扩大2倍 C、缩小 D、不能确定5. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,下列式子正确的是( )
 A、sinA= B、cosA= C、tanA= D、cosB=6. 如图,在菱形ABCD中,AC=8,BD=6,DE⊥AB,垂足为E,DE与AC交于点F,则sin∠DFC的值为( )
A、sinA= B、cosA= C、tanA= D、cosB=6. 如图,在菱形ABCD中,AC=8,BD=6,DE⊥AB,垂足为E,DE与AC交于点F,则sin∠DFC的值为( ) A、 B、 C、 D、7. 如图,△ABC中AB=AC=4,∠C=72°,D是AB中点,点E在AC上,DE⊥AB,则cosA的值为( )
A、 B、 C、 D、7. 如图,△ABC中AB=AC=4,∠C=72°,D是AB中点,点E在AC上,DE⊥AB,则cosA的值为( ) A、 B、 C、 D、8. 如图,在正方形方格纸中,每个小方格边长为1,A,B,C,D都在格点处,AB与CD相交于点O,则sin∠BOD的值等于( )
A、 B、 C、 D、8. 如图,在正方形方格纸中,每个小方格边长为1,A,B,C,D都在格点处,AB与CD相交于点O,则sin∠BOD的值等于( ) A、 B、 C、 D、9. 如图,已知扇形OAB的半径为r,C是弧AB上的任一点(不与A,B重合),CM⊥OA,垂足为M,CN⊥OB,垂足为N,连接MN,若∠AOB= ,则MN可用 表示为( )
A、 B、 C、 D、9. 如图,已知扇形OAB的半径为r,C是弧AB上的任一点(不与A,B重合),CM⊥OA,垂足为M,CN⊥OB,垂足为N,连接MN,若∠AOB= ,则MN可用 表示为( )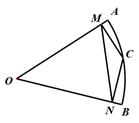 A、 B、 C、 D、10. 如图,在▱ABCD中,∠DAB=60°,AB=8,AD=6.⊙O分别切边AB,AD于点E,F,且圆心O好落在DE上.现将⊙O沿AB方向滚动到与BC边相切(点O在ABCD的内部),则圆心O移动的路径长为( )
A、 B、 C、 D、10. 如图,在▱ABCD中,∠DAB=60°,AB=8,AD=6.⊙O分别切边AB,AD于点E,F,且圆心O好落在DE上.现将⊙O沿AB方向滚动到与BC边相切(点O在ABCD的内部),则圆心O移动的路径长为( )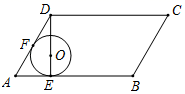 A、2 B、4 C、5﹣ D、8﹣2
A、2 B、4 C、5﹣ D、8﹣2二、填空题
-
11. 在Rt△ABC中,∠C=90°,BC=5,AC=12,则sinB的值是.12. 已知 中, 则边 的长度为 .13. 如图,点 在钝角 的边 上,连接 , , , ,则 的余弦值为 .
 14. 如图,在△ABC中,∠BAC=90°,AB=AC=5,将△ABC折叠,使点B落在AC边上的点D处,EF为折痕,若sin∠CFD的值为 ,则BE=.
14. 如图,在△ABC中,∠BAC=90°,AB=AC=5,将△ABC折叠,使点B落在AC边上的点D处,EF为折痕,若sin∠CFD的值为 ,则BE=.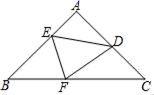 15. 如图,在△ABC中,AD、BE分别是边BC、AC上的中线,AB=AC=5,cos∠C= ,那么GE= .
15. 如图,在△ABC中,AD、BE分别是边BC、AC上的中线,AB=AC=5,cos∠C= ,那么GE= .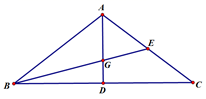 16. 如图,在Rt△ABC中,AC=8,BC=6,若点M、N分别是线段AB、AC上的两个动点,则CM+MN的最小值为.
16. 如图,在Rt△ABC中,AC=8,BC=6,若点M、N分别是线段AB、AC上的两个动点,则CM+MN的最小值为. 17. 如图,在 中, , , ,用含 和 的代数式表示 的值为:.
17. 如图,在 中, , , ,用含 和 的代数式表示 的值为:. 18. 数学研究性学习小组制作了如下的三角函数计算图尺:在半径为1的半圆形量角器中,画一个直径为1的圆,把刻度尺CA的0刻度固定在半圆的圆心O处,刻度尺可以绕点O旋转.从图中所示的图尺可读出sin∠AOB的值是.
18. 数学研究性学习小组制作了如下的三角函数计算图尺:在半径为1的半圆形量角器中,画一个直径为1的圆,把刻度尺CA的0刻度固定在半圆的圆心O处,刻度尺可以绕点O旋转.从图中所示的图尺可读出sin∠AOB的值是.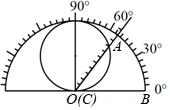
三、解答题
-
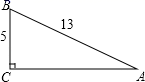
19. 如图,在Rt△ABC中,a=5,c=13,求sinA,cosA,tanA.
 20. 如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,求cos∠EFC的值.
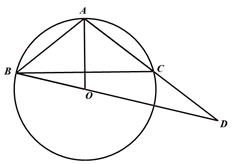
20. 如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,求cos∠EFC的值. 21. 如图,CB是⊙O的直径,P是CB延长线上一点,PB=2,PA切⊙O于A点,PA=4,求cosP.
21. 如图,CB是⊙O的直径,P是CB延长线上一点,PB=2,PA切⊙O于A点,PA=4,求cosP. 22. 如图,在△ABC中,AB=AC,BC=12,sinC= ,点G是△ABC的重心,线段BG的延长线交边AC于点D,求∠CBD的余弦值.
22. 如图,在△ABC中,AB=AC,BC=12,sinC= ,点G是△ABC的重心,线段BG的延长线交边AC于点D,求∠CBD的余弦值. 23. 如图,定义:在直角三角形ABC中,锐角α的邻边与对边的比叫做角α的余切,记作ctanα,即ctanα= = ,根据上述角的余切定义,解下列问题:
23. 如图,定义:在直角三角形ABC中,锐角α的邻边与对边的比叫做角α的余切,记作ctanα,即ctanα= = ,根据上述角的余切定义,解下列问题: (1)、ctan30°=;(2)、如图,已知tanA= ,其中∠A为锐角,试求ctanA的值.24. 如图,△ABC中,AB=AC=13,BD⊥AC于点D,sinA=
(1)、ctan30°=;(2)、如图,已知tanA= ,其中∠A为锐角,试求ctanA的值.24. 如图,△ABC中,AB=AC=13,BD⊥AC于点D,sinA= (1)、求BD的长;(2)、求tanC的值.25. 如图,已知 ,以 为直径的 交 于点 ,点 为弧 的中点,连接 交 于点 .且 .
(1)、求BD的长;(2)、求tanC的值.25. 如图,已知 ,以 为直径的 交 于点 ,点 为弧 的中点,连接 交 于点 .且 .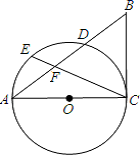 (1)、求证: 是 的切线;(2)、若 的半径为4, ,求 的长.26. 如图,AB是 的直径,D是 的中点, 于E,交CB于点 过点D作BC的平行线DM,连接AC并延长与DM相交于点G.
(1)、求证: 是 的切线;(2)、若 的半径为4, ,求 的长.26. 如图,AB是 的直径,D是 的中点, 于E,交CB于点 过点D作BC的平行线DM,连接AC并延长与DM相交于点G.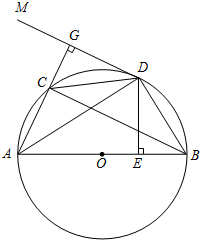 (1)、求证:GD是 的切线;(2)、求证: ;(3)、若 , ,求 的值.
(1)、求证:GD是 的切线;(2)、求证: ;(3)、若 , ,求 的值.