初中数学苏科版九年级下册7.1 正切 同步训练
试卷更新日期：2021-04-01 类型：同步测试
一、单选题
-
1. 在 中， ， ， ，则 的值为（ ）A、 B、 C、 D、2. 在Rt△ABC中，∠C＝90°，各边都扩大5倍，则tanA的值（ ）A、不变 B、扩大5倍 C、缩小5倍 D、不能确定3. 如图，直线OA过点（2，1），直线OA与x轴的夹角为α，则tanα的值为（ ）
A、 B、 C、2 D、4. 如图，在数学兴趣小组探究活动中，小明要测量小河两岸相对的两点P，A的距离，他和同学利用工具测得PC=50米，∠PCA= ，根据上述测量数据可计算得到小河宽度PA为（ ）
A、 米 B、50 米 C、 米 D、50tanα米5. 如图，在 中， 于点 ，若 ，则 的值为（ ）
A、 B、 C、 D、6. 如图，点O为坐标原点，点A的坐标为（3，0），点B的坐标为（0，4），圆D过A，B，O三点，点C为弧OBA上的一点（不与O、A两点重合），连接OC，AC，则tanC的值为（ ）
A、 B、 C、 D、7. 如图， 的顶点都是正方形网格中的格点，则 等于（ ）
A、 B、 C、 D、8. 如图，在边长相同的小正方形网格中，点A、B、C、D都在这些小正方形的顶点上，AB与CD相交于点P，则tan∠APD的值为（ ）
A、2 B、 C、3 D、9. 如图，菱形 的顶点A在反比例函数 的图象上， ∥轴，边 、 分别交x轴于点E、F，若 ， ， ，则k值为（ ）
A、-12 B、-6 C、-18 D、610. 如图，Rt△AOB中，∠AOB＝90°，且点A在反比例函数 的图象上，点B在反比例函数 的图象上，则tanB的值是（ ）
A、 B、 C、 D、二、填空题
-
11. 如图，在平面直角坐标系xOy中，已知点A（3，3）和点B（7，0），则tan∠ABO＝.
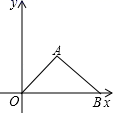12. 如图， 的顶点都是正方形网格中的格点，则 .
13. 如图，四边形ABCD是圆O的内接四边形，AC⊥BD交于点P，半径R＝6，BC＝8，则tan∠DCA＝.
14. 如图，CD是⊙O的直径，AB是⊙O的弦，CD⊥AB ， 垂足为E ， 连接BC、BD ． 点F为线段CB上一点，连接DF ， 若CE＝2，AB＝8，BF＝ ，则tan∠CDF＝ ．
15. 如图，在平面直角坐标系中，直线y＝﹣2x+4与x轴交于点A，与y轴交于点B，与直线y＝kx交于点C（4，n），则tan∠OCB的值为 ．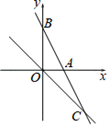
16. 如图，在矩形ABCD中，BD是对角线， ，垂足为E，连CE，若 ，则 ．
17. 如图，在矩形ABCD中，点E是边BC的中点，AE⊥BD，垂足为F，则tan∠BDE的值是
18. 如图，在矩形ABCD中，AB＝5，BC＝3，将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF，点A落在矩形ABCD的边CD上，连结CE，CF，若∠CEF＝α，则tanα＝ ．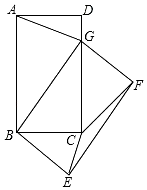
三、解答题
-
19. 如图，在三角形ABC中，∠ACB＝90°，CD⊥AB交AB于D，AD＝4，BD＝9，求tanA.
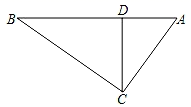20. 步行是全世界公认的有效、科学的健身方法.为了方便市民步行健身，某区园林部门决定将某公园里的一段斜坡 改造成 .已知原坡角 ，改造后的斜坡 的坡度为 ， 米，求原斜坡 的长．(精确到0.1米，参考数据： )
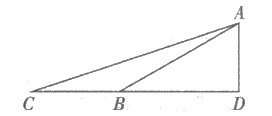21. 如图，⊙O是△ABC的外接圆，AB是直径，⊙O的切线PC交BA的延长线于点P，OF∥BC交AC于点E，交PC于点F，连接AF．
(1)、求证：AF是⊙O的切线；(2)、若AB=8，tanB= ，求线段CF、PC的长．22. 四边形ABCD内接于⊙O，AB是⊙O的直径，AD=CD。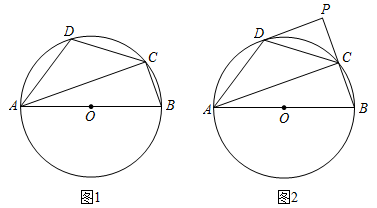
(1)、如图1，求证∠ABC=2∠ACD；(2)、过点D作⊙O的切线，交BC延长线于点P(如图2)。若tan∠CAB= ，BC=1，求PD的长。23. 如图，已知在△ABC中，点D是BC边上一点，DA⊥AB，AC=12，BD=7，CD=9.
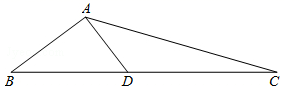(1)、求证：△ACD∽△BCA；(2)、求tan∠CAD的值.24. 如图，在Rt△ABC中，点O在斜边AB上，以O为圆心，OB为半径作圆，分别与BC，AB相交于点D，E，连结AD.已知∠CAD＝∠B.
(1)、求证：AD是⊙O的切线；(2)、若BC＝8，tanB＝ ， 求⊙O的半径.25. 在矩形ABCD中，E为 上的一点，把 沿AE翻折，使点D恰好落在BC边上的点F．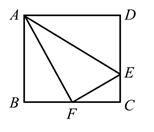
(1)、求证：(2)、若 ，求EC的长；(3)、若 ，记 ，求 的值．26.如图，在平面直角坐标系中，抛物线 与 轴交于A、B两点（点A在点B的左侧），点B的坐标为（3，0），与 轴交于点C（0，-3），顶点为D。
(1)、求抛物线的解析式及顶点D的坐标。(2)、联结AC，BC，求∠ACB的正切值。(3)、点P是x轴上一点，是否存在点P使得△PBD与△CAB相似，若存在，请求出点P的坐标；若不存在，请说明理由。(4)、M是抛物线上一点，点N在 轴，是否存在点N，使得以点A，C，M，N为顶点的四边形是平行四边形？若存在，请直接写出点N的坐标；若不存在，请说明理由。