初中数学湘教版七年级下学期期中复习专题2 代入消元法

试卷更新日期：2021-03-31 类型：复习试卷

进入出卷网下载

一、单选题

1. 用代入法解方程组 ${\begin{array}{l} y = 2 x - 3 ① \\ x - 2 y = 8 ② \end{array}$ 时，将方程①代入②中，所得的方程正确的是（）

A、x - 4x - 3 = 8 B、x - 4x - 6 = 8 C、x - 4x + 6 = 8 D、x + 4x - 3 = 8

查看试题解析
2. 若 ${\begin{cases} x = 3 - m \\ y = 1 + 2 m \end{cases}$ ，则y用只含x的代数式表示为（）

A、y=2x+7 B、y=7﹣2x C、y=﹣2x﹣5 D、y=2x﹣5

查看试题解析
3. 由方程组 ${\begin{matrix} x + m = 6 \\ y - 3 = m \end{matrix}$ 可得出x与y的关系式是（）

A、x+y=9 B、x+y=3 C、x+y=﹣3 D、x+y=﹣9

查看试题解析
4. 已知方程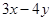组 ${\begin{matrix} x - y = 3 \\ 2 y + 3 (x - y) = 11 \end{matrix}$ ，那么代数式的值为（）

A、1 B、8 C、－1 D、－8

查看试题解析
5. 如果方程组 ${\begin{cases} 3 x + 7 y = 10 \\ a x + (a - 1) y = 5 \end{cases}$ 的解中的x与y的值相等，那么a的值是（）

A、1 B、2 C、3 D、4

查看试题解析
6. 使方程组 ${\begin{cases} 2 x + m y = 16 \\ x - 2 y = 0 \end{cases}$ 有自然数解的整数m（）

A、只有5个 B、只能是偶数 C、是小于16的自然数 D、是小于32的自然数

查看试题解析
7. 已知方程组 ${\begin{cases} 2 x + y = 1 + 3 m \\ x + 2 y = 1 - m \end{cases}$ 的解满足x+y＜0，则m的取值范围是（）

A、m＞﹣1 B、m＞1 C、m＜﹣1 D、m＜1

查看试题解析
8. 二元一次方程组 ${\begin{array}{l} x + y = 3 ， \\ 2 x = 4 y . \end{array}$ 的解是（）.

A、 ${\begin{array}{l} x = 3 \\ y = 0 \end{array}$ B、 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ C、 ${\begin{array}{l} x = 5 \\ y = - 2 \end{array}$ D、 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$

查看试题解析
9. 在方程组 ${\begin{array}{l} 3 x - y = 7 \\ x = y - 1 \end{array}$ 中，代入消元可得（）

A、3y–1–y=7 B、y–1–y=7 C、3y–3=7 D、3y–3–y=7

查看试题解析
10. 若方程组 ${\begin{cases} 2 k x + (k - 1) y = 3 \\ 4 x + 3 y = 1 \end{cases}$ 的解x和y互为相反数，则k的值为（）

A、2 B、－2 C、3 D、－3

查看试题解析
11. 用代入法解方程组 ${\begin{matrix} x = 2 y ① \\ 2 x - y = 5 ② \end{matrix}$ 较简单的方法是（）

A、由①得y= $\frac{1}{2}$ x，然后代入②消去y B、由②得y=2x﹣5，然后代入①消去y C、将①代入②消去x D、由②得x= $\frac{1}{2}$ （5+y），然后代入①消去x

查看试题解析

二、填空题

12. 若方程组 ${\begin{matrix} 2 x + 3 y = 1 \\ (k - 1) x + (k + 1) y = 4 \end{matrix}$ 的解 $x$ 与 $y$ 相等，则 $k$ 的值为．

查看试题解析
13. 若x，y满足方程组 ${\begin{array}{l} x + m = 7 \\ 2 y - 5 = m \end{array}$ 则无论m取何值 $3 x + 6 y - 1 =$ .

查看试题解析
14. 若满足方程组 ${\begin{array}{l} 3 x + y = m + 3 \\ 2 x - y = 2 m - 1 \end{array}$ 的x与y互为相反数，则m的值为．

查看试题解析
15. 已知 ${\begin{matrix} x = t \\ y = 2 t - 1 \end{matrix}$ ，用含x的代数式表示y得：y＝.

查看试题解析
16. 二元一次方程组 ${\begin{matrix} x = 3 \\ 2 x - y = 8 \end{matrix}$ 的解是．

查看试题解析

三、解答题

17. 用代入消元法解下列方程

(1)、 ${\begin{matrix} x - 2 y = 0 \\ x = 3 y + 1 \end{matrix}$

(2)、 ${\begin{matrix} y = x - 3 \\ y - 2 x = 5 \end{matrix}$

(3)、 ${\begin{matrix} 2 x - y = 5 \\ x + y = 1 \end{matrix}$

(4)、 ${\begin{matrix} x - 3 y = 5 \\ 2 x + y = 5 \end{matrix}$

(5)、 ${\begin{matrix} y = x - 3 \\ 2 x + 3 y = 6 \end{matrix}$

(6)、 ${\begin{matrix} 2 p - 3 q = 13 \\ - p + 5 = 4 q \end{matrix}$

查看试题解析
18. 已知方程组 ${\begin{matrix} x + 2 y = m + 1 \\ 2 x - y = 4 \end{matrix}$ 的解x，y的和等于2，
①求m的值.

②原方程组的解．

查看试题解析
19. 已知关于 $x ， y$ 的方程组 ${\begin{cases} x + 2 y = 1 ① \\ x - 2 y = m ② \end{cases}$ ，

(1)、若用代入法求解，可由①得： $x$ =③，把③代入②解得 $y$ = ，将其代入③解得 $x$ = ， ∴原方程组的解为；

(2)、若此方程组的解 $x ， y$ 互为相反数，求这个方程组的解及 $m$ 的值．

查看试题解析
20. 课本里，用代入法解二元一次方程组 ${\begin{matrix} x - y = 2 \\ 2 x + y = 7 \end{matrix}$ 的过程是用下面的框图表示：
根据以上思路，请用代入法求出方程组 ${\begin{matrix} x - y = 0 \\ | x - 2 y | = 2 \end{matrix}$ 的解（不用画框架图）.

查看试题解析