河南省许昌市禹州市2021年数学中考一模试卷

试卷更新日期：2021-03-30 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列方程中，属于一元二次方程的是（）

A、2y＝3x+2 B、3x²﹣1＝2x C、2x²﹣1＝ $\frac{1}{x}$ D、5＝x+3

查看试题解析
2. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列说法中，正确的是（）

A、“任意画一个多边形，其内角和是360°”是必然事件 B、“如果a²＝b² ，那么a＝b”是必然事件 C、可能性是50%的事件，是指在两次试验中一定有一次会发生 D、“从一副扑克牌（含大小王）中抽一张，恰好是红桃”是随机事件

查看试题解析
4. 如图，已知直线a∥b∥c，若AB＝9，BC＝6，DF＝10，则DE的长为（）

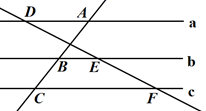A、4 B、5 C、6 D、7

查看试题解析
5. 如图，在△ABC中，∠BAC＝138°，将△ABC绕点A按逆时针方向旋转得到△AB'C'.若点B刚好落在BC边上，且AB'＝CB'，则∠C的度数为（）

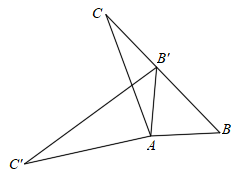A、16° B、15° C、14° D、13°

查看试题解析
6. 已知点A（a，m），B（a﹣1，n），C（3，﹣1）在反比例函数y＝ $\frac{k}{x}$ 的图象上.若a＞1，则m，n的大小关系是（）

A、m＜n B、m＞n C、m＝n D、m，n的大小不确定

查看试题解析
7. 已知关于 $x$ 的一元二次方程 $(m - 1) x^{2} - 2 x + 1 = 0$ 有两个实数根，则 $m$ 的取值范围是（）

A、 $m > 2$ B、 $m < 2$ C、 $m \geq 2$ D、 $m \leq 2$ ，且 $m \neq 1$

查看试题解析
8. 在一个不透明的袋子里装有红球，黄球共60个，这些球除颜色外其他都相同.小明通过多次试验发现，摸出红球的频率稳定在0.25左右，则袋子中红球的个数最有可能是（）

A、9 B、15 C、18 D、24

查看试题解析
9. 如图，点A是第一象限内双曲线y＝ $\frac{m}{x}$ （m＞0）上一点，过点A作AB∥x轴，交双曲线y＝ $\frac{n}{x}$ （n＜0）于点B，作AC∥y轴，交双曲线y＝ $\frac{n}{x}$ （n＜0）于点C，连接BC.若△ABC的面积为 $\frac{9}{2}$ ，则m，n的值不可能是（）

A、m＝ $\frac{1}{9}$ ，n＝﹣ $\frac{10}{9}$ B、m＝ $\frac{1}{4}$ ，n＝﹣ $\frac{5}{4}$ C、m＝1，n＝﹣2 D、m＝4，n＝﹣2

查看试题解析
10. 如图1，在等边三角形ABC和矩形DEFG中，AC＝DE，点C，D，G都在直线l上，且AC⊥l于点C，DE⊥l于点D，且D，B，E三点共线，将矩形DEFG以每秒1个单位长度的速度从左向右匀速运动，直至矩形DEFG和△ABC无重叠部分，设矩形DEFG运动的时间为t秒，矩形DEFG和△ABC重叠部分的面积为S，图2为S随t的变化而变化的函数图象，则函数图象中点H的纵坐标是（）

A、 $\frac{4}{3} \sqrt{3}$ B、 $2 \sqrt{3}$ C、 $\frac{8}{3} \sqrt{3}$ D、3 $\sqrt{3}$

查看试题解析

二、填空题

11. 若 $\frac{a}{a + b} = \frac{1}{3}$ ，则 $\frac{b}{a}$ 的值为.

查看试题解析
12. 如图，四边形ABCD内接于⊙O，若∠ADC＝120°，则∠AOC的度数为.

查看试题解析
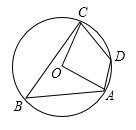13. 已知二次函数y＝ax²﹣4ax+c的图象与x轴交于A（﹣1，0），B两点，则点B的坐标为.

查看试题解析
14. 如图，在菱形ABCD中，∠B＝60°，E，H分别为AB，BC的中点，G，F分别为线段HD，CE的中点.若线段FG的长为2 $\sqrt{3}$ ，则AB的长为.

查看试题解析
15. 如图，将半径为2，圆心角为120°的扇形OAB绕点B逆时针旋转60°，得到扇形O'A'B，其中点A的运动路径为 $\overset{⌢}{A A^{'}}$ ，则图中阴影部分的面积为.

查看试题解析

三、解答题

16. 先化简，再求值： $(\frac{2}{x - 2} - \frac{2 x}{x^{2} - 4}) \div \frac{2 x - 4}{x^{2} - 4 x + 4}$ .其中x的值为一元二次方程 $x^{2} + 5 x + 6 = 0$ 的解.

查看试题解析

17. 某校在第五届全国学生“学宪法讲宪法”活动中举办了宪法知识竞赛，并从中选取了部分学生的竞赛成绩进行统计（满分100分，成绩均不低于50分），绘制了如下尚不完整的统计图表.

调查结果频数分布表

分数段/分	频数	频率
50≤x＜60	2	0.04
60≤x＜70	8	0.16
70≤x＜80	m	0.24
80≤x＜90	24	n
90≤x＜100	4	0.08

请根据以上信息，回答下列问题：

(1)、填空：m＝， n＝，本次抽取了名学生；

(2)、请补全频数分布直方图；

(3)、若甲同学的竞赛成绩是所有竞赛成绩的中位数，据此推测他的成绩落在分数段内；

(4)、竞赛成绩不低于90分的4名同学中正好有2名男生和2名女生，现准备从中随机选出2名同学参加市里面“学宪法讲宪法”演讲比赛，求正好抽到一男一女的概率.

查看试题解析

18. 某校数学实践社团开展了一次“利用数学知识测量学校操场上旗杆高度”的实践活动，该校九年级学生积极参与.小红和小华决定利用下午课间的时间，用测量影长的方式求出旗杆高度.同一时刻测量站在旗杆旁边的小红（CD）和旗杆AB的影长时，发现旗杆的影子一部分落在地面上（BF），另一部分落在了距离旗杆24m的教学楼上（EF）.经测量，小红落在地面上的影长DG为2.4m，教学楼上的影长EF为2m.已知小红的身高是1.6m，请根据小红和小华的测量结果，求出旗杆AB的高度.

查看试题解析
19. 临近新年，某玩具店计划购进一种玩具，其进价为30元/个，已知售价不能低于成本价.在销售过程中，发现该玩具每天的销售量y（个）与售价x（元/个）之间满足一次函数关系，y与x的几组对应值如表：

x

40

45

50

55

y

80

70

60

50

(1)、求y与x之间的函数关系式；

(2)、如果规定该玩具每天的销售量不低于46件，当该玩具的售价定为多少元/个时，每天获取的利润w最大，最大利润是多少？

查看试题解析
20. 如图，AC是⊙O的直径，点B是⊙O上一点，且BD＝BA，过点B作BE⊥DC，交DC的延长线于点E.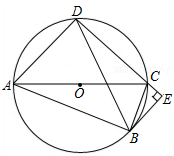

(1)、求证：BE是⊙O的切线；

(2)、若BE＝2CE，当AD＝6时，求BD的长.

查看试题解析
21. 如图，在平面直角坐标系xOy中，菱形ABCD的顶点B的坐标为（1，0），顶点C的坐标为（4，2），对角线AC∥x轴，边AB所在直线y₁＝ax+b与反比例函数y₂＝ $\frac{k}{x}$ （k＜0）的图象交于A，E两点；

(1)、求y₁和y₂的函数解析式；

(2)、当y₁＞y₂时，求x的取值范围；

(3)、点P是x轴上一动点，当△PAC是以AC为斜边的直角三角形时，请直接写出点P的坐标.

查看试题解析
22. 抛物线y＝x²﹣2ax﹣a﹣3与x轴交于点A，B，与y轴交于点C，点D（4，﹣a﹣3）在抛物线的图象上.

(1)、求抛物线的解析式；

(2)、现规定平面直角坐标系中横纵坐标相等的点为“不动点”.已知点N（x_N ， y_N），Q（x_Q ， y_Q）是抛物线y＝x²﹣2ax﹣a﹣3图象上的“不动点”，点H是点N，Q之间抛物线上一点（不与点N，Q重合），求点H的纵坐标的取值范围.

查看试题解析
23. 如图

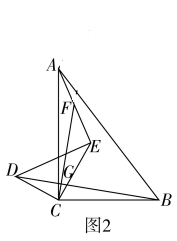(1)、如图1.在Rt△ACB中，∠ACB＝90°，AC＝8，BC＝6，点D、E分别在边CA，CB上且CD＝3，CE＝4，连接AE，BD，F为AE的中点，连接CF交BD于点G，则线段CG所在直线与线段BD所在直线的位置关系是.（提示：延长CF到点M，使FM＝CF，连接AM）

(2)、将△DCE绕点C逆时针旋转至图2所示位置时，（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由.

(3)、将△DCE绕点C逆时针在平面内旋转，在旋转过程中，当B，D，E三点在同一条直线上时，CF的长为.

查看试题解析