河南省2021年数学中考二模试卷
试卷更新日期:2021-03-30 类型:中考模拟
一、单选题
-
1. 已知直线 及一点P,要过点P作一直线与 平行,那么这样的直线( )A、有且只有一条 B、有两条 C、不存在 D、不存在或者只有一条2. 下列运算中正确的是( )A、 B、 C、 D、3. 若 则m的值为( )A、2 B、3 C、4 D、54. 是⊙ 的直径, 切⊙ 于点 , 交⊙ 于点 ;连接 ,若 ,则 等于( )
 A、20° B、25° C、30° D、40°5. 若 ,则 的值是( )A、4 B、3 C、2 D、16. 如图是与 位似的三角形的几种画法,其中正确的有( )
A、20° B、25° C、30° D、40°5. 若 ,则 的值是( )A、4 B、3 C、2 D、16. 如图是与 位似的三角形的几种画法,其中正确的有( )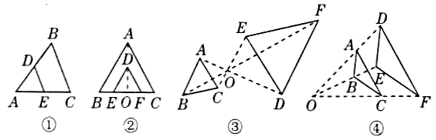 A、1个 B、2个 C、3个 D、4个7. 某经销商销售一批电话手表,第一个月以550元/块的价格售出60块,第二个月起降价,以500元/块的价格将这批电话手表全部售出,销售总额超过了5.5万元.这批电话手表至少有( )A、103块 B、104块 C、105块 D、106块8. 在公园内,牡丹按正方形种植,在它的周围种植芍药,如图反映了牡丹的列数(n)和芍药的数量规律,那么当n=11时,芍药的数量为( )
A、1个 B、2个 C、3个 D、4个7. 某经销商销售一批电话手表,第一个月以550元/块的价格售出60块,第二个月起降价,以500元/块的价格将这批电话手表全部售出,销售总额超过了5.5万元.这批电话手表至少有( )A、103块 B、104块 C、105块 D、106块8. 在公园内,牡丹按正方形种植,在它的周围种植芍药,如图反映了牡丹的列数(n)和芍药的数量规律,那么当n=11时,芍药的数量为( ) A、84株 B、88株 C、92株 D、121株9. 如图,小明想要测量学校操场上旗杆 的高度,他作了如下操作:(1)在点C处放置测角仪,测得旗杆顶的仰角 ;(2)量得测角仪的高度 ;(3)量得测角仪到旗杆的水平距离 .利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )
A、84株 B、88株 C、92株 D、121株9. 如图,小明想要测量学校操场上旗杆 的高度,他作了如下操作:(1)在点C处放置测角仪,测得旗杆顶的仰角 ;(2)量得测角仪的高度 ;(3)量得测角仪到旗杆的水平距离 .利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )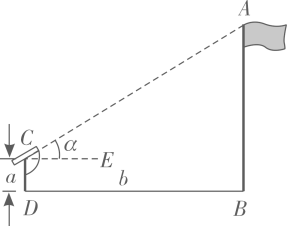 A、 B、 C、 D、10. 若数 使关于 的分式方程 有正数解,且使关于 的不等式组 有解,则所有符合条件的整数 的个数为( )A、1 B、2 C、3 D、411. 如图,在△ABC中,AB=AC,AE平分∠BAC,DE垂直平分AB,连接CE,∠B=70°.则∠BCE的度数为( )
A、 B、 C、 D、10. 若数 使关于 的分式方程 有正数解,且使关于 的不等式组 有解,则所有符合条件的整数 的个数为( )A、1 B、2 C、3 D、411. 如图,在△ABC中,AB=AC,AE平分∠BAC,DE垂直平分AB,连接CE,∠B=70°.则∠BCE的度数为( ) A、55° B、50° C、40° D、35°12.
A、55° B、50° C、40° D、35°12.如图,在平面直角坐标系中,反比例函数y= (x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
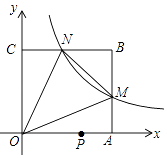 A、6 B、10 C、2 D、2
A、6 B、10 C、2 D、2二、填空题
-
13. 计算 的结果是.14. 纳秒 是非常小的时间单位, ,北斗全球导航系统的授时精度优于 ,用科学记数法表示 是 .15. 不透明袋子中装有8个球,其中有3个红球、5个黑球,这些球除颜色外无其他差别.从袋子中随机取出1个球,则它是红球的概率是 .16. 如图,在Rt△ABC中,∠ACB=90°,∠CAB=60°,AC=1,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE, 点B经过的路径为弧BD,则图中阴影部分的面积为.
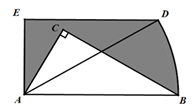 17. 甲、乙两车分别从A、B两地同时出发,相向行驶,已知甲车的速度大于乙车的速度,甲车到达B地后马上以另一速度原路返回A地(掉头的时间忽略不计),乙车到达A地以后即停在地等待甲车.如图所示为甲乙两车间的距离y(千米)与甲车的行驶时间t(小时)之间的函数图象,则当乙车到达A地的时候,甲车与A地的距离为千米.
17. 甲、乙两车分别从A、B两地同时出发,相向行驶,已知甲车的速度大于乙车的速度,甲车到达B地后马上以另一速度原路返回A地(掉头的时间忽略不计),乙车到达A地以后即停在地等待甲车.如图所示为甲乙两车间的距离y(千米)与甲车的行驶时间t(小时)之间的函数图象,则当乙车到达A地的时候,甲车与A地的距离为千米.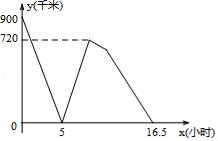 18. 某班级从文化用品市场购买签字笔和圆珠笔共15支,所付金额大于26元,但小于27元,已知签字笔每支2元,圆珠笔每支1.5元,则其中签字笔购买了支.
18. 某班级从文化用品市场购买签字笔和圆珠笔共15支,所付金额大于26元,但小于27元,已知签字笔每支2元,圆珠笔每支1.5元,则其中签字笔购买了支.三、解答题
-
19. 先化简,再求值: ,其中x是不等式组 的整数解.20. 如图,平行四边形 的对角线交于点 ,分别以 , 为邻边作平行四边形 , 交 于点 ,连结 .
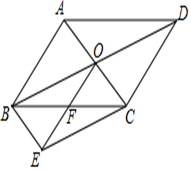 (1)、求证: 为 中点;(2)、若 ⊥ , ,求平行四边形 的周长.21. 病毒虽无情,人间有大爱.2020年,在湖北省抗击新冠病毒的战“疫”中,全国(除湖北省外)共有30个省(区、市)及军队的医务人员在党中央全面部署下,白衣执甲,前赴后继支援湖北省.全国30个省(区、市)各派出支援武汉的医务人员频数分布直方图(不完整)和扇形统计图如下:(数据分成6组: , , , , , .)
(1)、求证: 为 中点;(2)、若 ⊥ , ,求平行四边形 的周长.21. 病毒虽无情,人间有大爱.2020年,在湖北省抗击新冠病毒的战“疫”中,全国(除湖北省外)共有30个省(区、市)及军队的医务人员在党中央全面部署下,白衣执甲,前赴后继支援湖北省.全国30个省(区、市)各派出支援武汉的医务人员频数分布直方图(不完整)和扇形统计图如下:(数据分成6组: , , , , , .)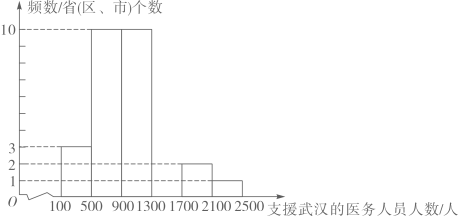
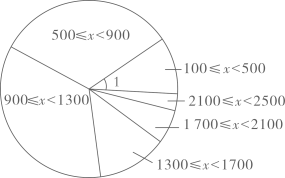
根据以上信息回答问题:
(1)、补全频数分布直方图.(2)、求扇形统计图中派出人数大于等于100小于500所占圆心角度数.据新华网报道在支援湖北省的医务人员大军中,有“90后”也有“00后”,他们是青春的力量,时代的脊梁.小华在收集支援湖北省抗疫宣传资料时得到这样一组有关“90后”医务人员的数据:
市派出的1614名医护人员中有404人是“90后”;
市派出的338名医护人员中有103人是“90后”;
市某医院派出的148名医护人员中有83人是“90后”.
(3)、请你根据小华得到的这些数据估计在支援湖北省的全体医务人员(按4.2万人计)中,“90后”大约有多少万人?(写出计算过程,结果精确到0.1万人)22. 阅读下列材料解答问题:新定义:对非负数x“四舍五入”到个位的值记为<x>,即:当n为非负整数时,如果n﹣ ≤x<n+ ,则<x>=n;反之,当n为非负整数时,如果<x>=n,则n﹣ ≤x<n+ .例如:<0.1>=<0.49>=0,<1.51>=<2.48>=2,<3>=3,<4.5>=<5.25>=5,…试解决下列问题:(1)、①<π+2.4>=(π为圆周率);②如果<x﹣1>=2,则数x的取值范围为;(2)、求出满足<x>= x﹣1的x的取值范围.23. 如图, 中, ,顶点A,B都在反比例函数 的图象上,直线 轴,垂足为D,连结 , ,并延长 交 于点E,当 时,点E恰为 的中点,若 , .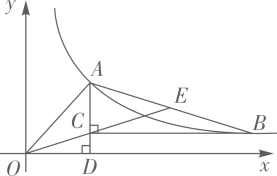 (1)、求反比例函数的解析式;(2)、求 的度数.24. 某电器超市销售每台进价分别为160元、120元的A、B两种型号的电风扇,如表是近两周的销售情况:
(1)、求反比例函数的解析式;(2)、求 的度数.24. 某电器超市销售每台进价分别为160元、120元的A、B两种型号的电风扇,如表是近两周的销售情况:销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3台
4台
1200元
第二周
5台
6台
1900元
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)、求A、B两种型号的电风扇的销售单价;(2)、若超市准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?(3)、在(2)的条件下,超市销售完这50台电风扇能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.25. 如图,在平面直角坐标系中,抛物线 与x轴正半轴交于点A,且点A的坐标为 ,过点A作垂直于x轴的直线l.P是该抛物线上的任意一点,其横坐标为m,过点P作 于点Q;M是直线l上的一点,其纵坐标为 ,以 , 为边作矩形 . (1)、求b的值.(2)、当点Q与点M重合时,求m的值.(3)、当矩形 是正方形,且抛物线的顶点在该正方形内部时,求m的值.(4)、当抛物线在矩形 内的部分所对应的函数值y随x的增大而减小时,直接写出m的取值范围.26. 如图,在等边三角形ABC中,BC=8,过BC边上一点P,作∠DPE=60°,分别与边AB,AC相交于点D与点E.
(1)、求b的值.(2)、当点Q与点M重合时,求m的值.(3)、当矩形 是正方形,且抛物线的顶点在该正方形内部时,求m的值.(4)、当抛物线在矩形 内的部分所对应的函数值y随x的增大而减小时,直接写出m的取值范围.26. 如图,在等边三角形ABC中,BC=8,过BC边上一点P,作∠DPE=60°,分别与边AB,AC相交于点D与点E.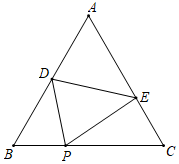 (1)、在图中找出与∠EPC始终相等的角,并说明理由;(2)、若△PDE为正三角形时,求BD+CE的值;(3)、当DE∥BC时,请用BP表示BD,并求出BD的最大值.
(1)、在图中找出与∠EPC始终相等的角,并说明理由;(2)、若△PDE为正三角形时,求BD+CE的值;(3)、当DE∥BC时,请用BP表示BD,并求出BD的最大值.