四川省达州市通川区2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-03-30 类型:期末考试
一、单选题
-
1. 在实数 ,0.31, ,-1, , 中,无理数有( )A、1个 B、2个 C、3个 D、4个2. 下列关于 的说法中,错误的是( )A、 是无理数 B、 C、5的平方根是 D、3. 甲、乙、丙、丁四名同学在一次投掷实心球训练中,在相同条件下各投掷10次,他们成绩的平均数 与方差 如下表:
甲
乙
丙
丁
平均数 (米)
11.1
11.1
10.9
10.9
方差
1.1
1.2
1.3
1.4
若要选一名成绩好且发挥稳定的同学参加比赛,则应该选择( )
A、甲 B、乙 C、丙 D、丁4. 若点M (a,b)在第四象限,则点N (–a,–b + 2)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 下列四个命题中,真命题有( )①两条直线被第三条直线所截,内错角相等.
②如果∠1和∠2是对顶角,那么∠1=∠2.
③三角形的一个外角大于任何一个内角.
④如果x2>0,那么x>0.
A、1个 B、2个 C、3个 D、4个6. 如图,∠A、∠1、∠2的大小关系是( ) A、∠A>∠1>∠2 B、∠2>∠1>∠A C、∠A>∠2>∠1 D、∠2>∠A>∠17. 如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列选项正确的是( )
A、∠A>∠1>∠2 B、∠2>∠1>∠A C、∠A>∠2>∠1 D、∠2>∠A>∠17. 如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列选项正确的是( )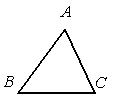 A、
A、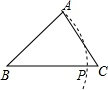 B、
B、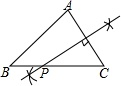 C、
C、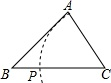 D、
D、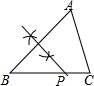 8. 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,那么小巷的宽度为( )
8. 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,那么小巷的宽度为( ) A、0.7米 B、1.5米 C、2.2米 D、2.4米9. 若实数k、b满足k+b=0,且k<b,则一次函数y=kx+b的图象可能是( )A、
A、0.7米 B、1.5米 C、2.2米 D、2.4米9. 若实数k、b满足k+b=0,且k<b,则一次函数y=kx+b的图象可能是( )A、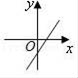 B、
B、 C、
C、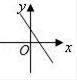 D、
D、 10. 如图,在正方形 外取一点 ,连接 , , .过点 作 的垂线交 于点 .若 , .下列结论:
10. 如图,在正方形 外取一点 ,连接 , , .过点 作 的垂线交 于点 .若 , .下列结论:
① ;②点 到直线 的距离为 ;③ ;④ ;⑤ .其中正确结论的序号是( )
A、①②③ B、①②④ C、①③⑤ D、②③⑤二、填空题
-
11. 的相反数是 .12. 已知点 , 是一次函数 图象上的两点,则 .(填“>”、“<”或“=”)13. 如图,已知 , , ,则 .
 14. 若 是二元一次方程组 的解,则 .15. 如图,Rt△ABC中,AC=5,BC=2.5,∠ACB=90°,分别以AB,BC,AC为直径作三个半圆,那么阴影部分的面积为.
14. 若 是二元一次方程组 的解,则 .15. 如图,Rt△ABC中,AC=5,BC=2.5,∠ACB=90°,分别以AB,BC,AC为直径作三个半圆,那么阴影部分的面积为. 16. 对于每个非零自然数 , 轴上有 , 两点,以 表示这两点间的距离,其中 , 的横坐标分别是方程组 的解,则 的值等于.
16. 对于每个非零自然数 , 轴上有 , 两点,以 表示这两点间的距离,其中 , 的横坐标分别是方程组 的解,则 的值等于.三、解答题
-
17. 为了了解某学校八年级学生每周平均体育锻炼时间的情况,随机抽查了该年级的部分学生,对其每周锻炼时间进行统计,根据统计数据绘制成图1和图2两个不完整的统计图.请你根据统计图提供的信息,回答下列问题:
 (1)、本次共抽取了学生人,并请将图1条形统计图补充完整;(2)、这组数据的中位数是 , 求出这组数据的平均数;(3)、若八年级有学生1800人,请你估计体育锻炼时间为3小时的学生有多少人?18. 已知:△ABC在平面直角坐标系中的位置如图所示.
(1)、本次共抽取了学生人,并请将图1条形统计图补充完整;(2)、这组数据的中位数是 , 求出这组数据的平均数;(3)、若八年级有学生1800人,请你估计体育锻炼时间为3小时的学生有多少人?18. 已知:△ABC在平面直角坐标系中的位置如图所示.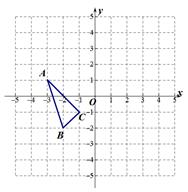 (1)、画出△ABC关于y轴对称的图形△A1B1C1;(2)、求△ABC的面积.19. 小明的妈妈在菜市场买回3斤萝卜、2斤排骨,准备做萝卜排骨汤.
(1)、画出△ABC关于y轴对称的图形△A1B1C1;(2)、求△ABC的面积.19. 小明的妈妈在菜市场买回3斤萝卜、2斤排骨,准备做萝卜排骨汤.妈妈:“今天买这两样菜共花了45元,上月买同重量的这两样菜只要36元”;
爸爸:“报纸上说了萝卜的单价上涨50%,排骨单价上涨20%”;
小明:“爸爸、妈妈,我想知道今天买的萝卜和排骨的单价分别是多少?”
请你通过列方程(组)求解这天萝卜、排骨的单价(单位:元/斤).
20. 如图, 是等边三角形,过 边上点 作 ,交 于点 ,在 的延长线上取点 ,使 ,连接 . (1)、求证: ;(2)、过 作 ,交 于点 ,求证: .21. 如图,直线 : 分别与x轴,y轴交于点D,点A,直线 : 与x轴交于点C,两直线 , 相交于点B,连AC.
(1)、求证: ;(2)、过 作 ,交 于点 ,求证: .21. 如图,直线 : 分别与x轴,y轴交于点D,点A,直线 : 与x轴交于点C,两直线 , 相交于点B,连AC. (1)、求点B的坐标和直线AC的解析式;(2)、求 的面积.22. 为表彰在某活动中表现积极的同学,老师决定购买文具盒与钢笔作为奖品.已知5个文具盒、2支钢笔共需100元;3个文具盒、1支钢笔共需57元.(1)、每个文具盒、每支钢笔各多少元?(2)、若本次表彰活动,老师决定购买10件作为奖品,若购买 个文具盒,10件奖品共需 元,求 与 的函数关系式.如果至少需要购买3个文具盒,本次活动老师最多需要花多少钱?23. 我们新定义一种三角形:两边平方和等于第三边平方的4倍的三角形叫做常态三角形.例如:某三角形三边长分别是5,6和8,因为62+82=4×52=100,所以这个三角形是常态三角形.
(1)、求点B的坐标和直线AC的解析式;(2)、求 的面积.22. 为表彰在某活动中表现积极的同学,老师决定购买文具盒与钢笔作为奖品.已知5个文具盒、2支钢笔共需100元;3个文具盒、1支钢笔共需57元.(1)、每个文具盒、每支钢笔各多少元?(2)、若本次表彰活动,老师决定购买10件作为奖品,若购买 个文具盒,10件奖品共需 元,求 与 的函数关系式.如果至少需要购买3个文具盒,本次活动老师最多需要花多少钱?23. 我们新定义一种三角形:两边平方和等于第三边平方的4倍的三角形叫做常态三角形.例如:某三角形三边长分别是5,6和8,因为62+82=4×52=100,所以这个三角形是常态三角形.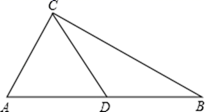 (1)、若 三边长分别是2, 和4,则此三角形常态三角形(填“是”或“不是”);(2)、若 是常态三角形,则此三角形的三边长之比为(请按从小到大排列);(3)、如图, 中,∠ACB=90°,BC=6,AD=DB=DC,若 是常态三角形,求 的面积.24. 如图,直线 与 轴相交于点 ,直线 经过点 ,与 轴交于点 ,与 轴交于点 ,与直线 相交于点 .
(1)、若 三边长分别是2, 和4,则此三角形常态三角形(填“是”或“不是”);(2)、若 是常态三角形,则此三角形的三边长之比为(请按从小到大排列);(3)、如图, 中,∠ACB=90°,BC=6,AD=DB=DC,若 是常态三角形,求 的面积.24. 如图,直线 与 轴相交于点 ,直线 经过点 ,与 轴交于点 ,与 轴交于点 ,与直线 相交于点 . (1)、求直线 的函数关系式;(2)、点 是 上的一点,若 的面积等于 的面积的 倍,求点 的坐标.(3)、设点 的坐标为 ,是否存在 的值使得 最小?若存在,请求出点 的坐标;若不存在,请说明理由.
(1)、求直线 的函数关系式;(2)、点 是 上的一点,若 的面积等于 的面积的 倍,求点 的坐标.(3)、设点 的坐标为 ,是否存在 的值使得 最小?若存在,请求出点 的坐标;若不存在,请说明理由.