浙江省宁波市奉化区2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-03-30 类型:期末考试
一、单选题
-
1. 若 则 ( )A、 B、 C、 D、2. 下列事件中,属于不可能事件的是( )A、明天会下雪 B、抛一枚硬币,正面朝上 C、小明购买一张彩票,一定中奖 D、在一个装有白球的袋子中摸出黑球3. 抛物线 的顶点坐标是( )A、 B、 C、 D、4. 已知圆的半径为 扇形的圆心角为 ,则扇形的面积为( )A、 B、 C、 D、5. 在Rt△ABC中,∠C=90°,AB=5,BC=3,则tanA的值是( )A、 B、 C、 D、6. 已知 , , 是抛物线 上的点,则( )A、 B、 C、 D、7. 如图,已知⊙O的半径为 ,弦 垂足为E,且 ,则 的长为( )
 A、 B、 C、 D、8. 下列命题:①任意三点确定一个圆;②平分弦(不是直径)的直径垂直于弦;③相等的圆心角所对的弦相等;④长度相等的弧是等弧.其中真命题的有( )A、 个 B、 个 C、 个 D、 个9. 如图,二次函数 的图象与x轴交于 两点,与y轴负半轴交于点C,它的对称轴为直线 ,则下列选项中正确的是( )
A、 B、 C、 D、8. 下列命题:①任意三点确定一个圆;②平分弦(不是直径)的直径垂直于弦;③相等的圆心角所对的弦相等;④长度相等的弧是等弧.其中真命题的有( )A、 个 B、 个 C、 个 D、 个9. 如图,二次函数 的图象与x轴交于 两点,与y轴负半轴交于点C,它的对称轴为直线 ,则下列选项中正确的是( ) A、 B、 C、 D、当 为实数)时,10. 一个矩形按如图1的方式分割成三个直角三角形,把较大两个直角三角形纸片按图2中①、②两种方式放置,设①中的阴影部分面积为 ,②中的阴影部分面积为 ,当 时,则矩形的两边之比为( )
A、 B、 C、 D、当 为实数)时,10. 一个矩形按如图1的方式分割成三个直角三角形,把较大两个直角三角形纸片按图2中①、②两种方式放置,设①中的阴影部分面积为 ,②中的阴影部分面积为 ,当 时,则矩形的两边之比为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
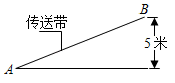
11. 正六边形的每个内角等于°.12. 一个封闭的箱子里装有 只白色小球, 只黑色小球,每只小球除颜色外均相同,从中任意拿出一只小球,则拿出小球为黑色的概率是.13. 如图,传送带把物体从地面送到离地面5米高的地方,如果传送带与地面所成的斜坡的坡度i=1:2.4,那么物体所经过的路程AB为米.
 14. 抛物线 向右平移一个单位得到的抛物线恰好经过原点,则 .15. 如图,在边长为 的正方形 中,E为 的中点.现将线段 绕着点B旋转得 .当 落在 上时,则 的长为.
14. 抛物线 向右平移一个单位得到的抛物线恰好经过原点,则 .15. 如图,在边长为 的正方形 中,E为 的中点.现将线段 绕着点B旋转得 .当 落在 上时,则 的长为. 16. 如图,在 中, 平分 在 延长线上,且 ,若 , ,则 的长为.
16. 如图,在 中, 平分 在 延长线上,且 ,若 , ,则 的长为.
三、解答题
-
17.(1)、计算: .(2)、已知 ,求 的值.18. “学习强国”学习平台是以习近平新时代中国特色社会主义思想和党的十九大精神为主要内容的优质平台,平台由PC端、手机端两大终端组成,手机客户端上主要由阅读文章、观看视频、答题活动三种学习方式(1)、王老师从三种学习方式中随机挑选一种进行学习,恰好选中答题活动的概率是多少?(2)、王老师和李老师各自从三种学习方式中随机挑选一种进行学习,用列表或画树状图的方法列出所有等可能的结果,并求他们选中同一种学习方式的概率.19. 如图所示,一艘轮船在近海处由西向东航行,点C处有一灯塔,灯塔附近30海里的圆形区域内有暗礁,轮船在A处测得灯塔在北偏东60°方向上,轮船又由A向东航行40海里到B处,测得灯塔在北偏东30°方向上.
 (1)、求轮船在B处时到灯塔C处的距离是多少?(2)、若轮船继续向东航行,有无触礁危险?20. 如图是 的正方形网格, 的三个顶点均在格点上.(1)、将 绕点 顺时针方向旋转 得到 ,在图①中作出 ;
(1)、求轮船在B处时到灯塔C处的距离是多少?(2)、若轮船继续向东航行,有无触礁危险?20. 如图是 的正方形网格, 的三个顶点均在格点上.(1)、将 绕点 顺时针方向旋转 得到 ,在图①中作出 ; (2)、在图②中作格点 ,使 ,且周长比为 ;
(2)、在图②中作格点 ,使 ,且周长比为 ; (3)、在图③中作一个与 相似且面积最大的格点 .
(3)、在图③中作一个与 相似且面积最大的格点 . 21. 如图,四边形 内接于⊙O,AB是直径,点D是 的中点.
21. 如图,四边形 内接于⊙O,AB是直径,点D是 的中点.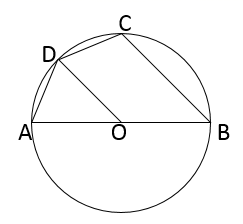 (1)、求证: ;(2)、连结 ,若 ,求 的长.22. 某网店销售一批商品,平均每天可售出 件,每件盈利 元.为了迎接“双十一”,尽快减少库存,网点决定采取降价促销活动.经调查发现,如果每件商品每降价 元,平均每天可多售出 件.设每件降价x元时,该网店一天可获利润y元.(1)、求y关于x的函数表达式;(2)、若网店每天平均盈利 元,则每件商品降价多少元?(3)、当每件商品降价多少元时,网店盈利最大?最大盈利多少元?23. 如图,抛物线 与x轴交于 两点,与y轴交于点 为顶点,连结 交x轴于点E.
(1)、求证: ;(2)、连结 ,若 ,求 的长.22. 某网店销售一批商品,平均每天可售出 件,每件盈利 元.为了迎接“双十一”,尽快减少库存,网点决定采取降价促销活动.经调查发现,如果每件商品每降价 元,平均每天可多售出 件.设每件降价x元时,该网店一天可获利润y元.(1)、求y关于x的函数表达式;(2)、若网店每天平均盈利 元,则每件商品降价多少元?(3)、当每件商品降价多少元时,网店盈利最大?最大盈利多少元?23. 如图,抛物线 与x轴交于 两点,与y轴交于点 为顶点,连结 交x轴于点E. (1)、求抛物线表达式;(2)、求 的度数;(3)、在y轴上是否存在一点P,使得 与 相似?若存在,求出P的坐标;若不存在,请说明理由.24. 定义:有两边之比为 的三角形叫做智慧三角形.(1)、如图1,在智慧三角形 中, 为 边上的中线,求 的值;
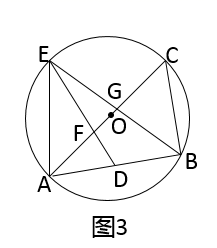
(1)、求抛物线表达式;(2)、求 的度数;(3)、在y轴上是否存在一点P,使得 与 相似?若存在,求出P的坐标;若不存在,请说明理由.24. 定义:有两边之比为 的三角形叫做智慧三角形.(1)、如图1,在智慧三角形 中, 为 边上的中线,求 的值;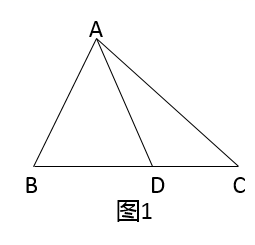 (2)、如图2, 是⊙O的内接三角形, 为直径,过 的中点D作 交线段 于点F,交⊙O于点E,连结 交 于点G.
(2)、如图2, 是⊙O的内接三角形, 为直径,过 的中点D作 交线段 于点F,交⊙O于点E,连结 交 于点G.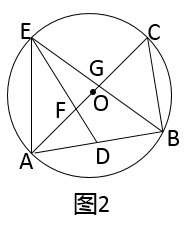
①求证: 是智慧三角形;
②设 ,若⊙O的半径为 ,求y关于x的函数表达式;
(3)、如图3,在(2)的条件下,当 时,求 的余弦值.