浙江省金华市义乌市2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-03-30 类型:期末考试
一、单选题
-
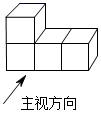
1. 一个数的相反数是-2020,则这个数是( )A、2020 B、-2020 C、 D、2. 用科学记数法表示439000,结果应为( )A、 B、 C、 D、3. 如图是由4个大小相同的正方体组合而成的几何体,其俯视图是( )
 A、
A、 B、
B、 C、
C、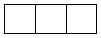 D、
D、 4. 在数轴上表示不等式﹣2≤x<4,正确的是( )A、
4. 在数轴上表示不等式﹣2≤x<4,正确的是( )A、 B、
B、 C、
C、 D、
D、 5. 已知两个有理数a,b,如果ab<0且a+b>0,那么( )A、a>0,b>0 B、a<0,b>0 C、a、b同号 D、a、b异号,且正数的绝对值较大6. 如图,已知四边形ABCD内接于⊙O,∠ABC=70°,则∠ADC的度数是( )
5. 已知两个有理数a,b,如果ab<0且a+b>0,那么( )A、a>0,b>0 B、a<0,b>0 C、a、b同号 D、a、b异号,且正数的绝对值较大6. 如图,已知四边形ABCD内接于⊙O,∠ABC=70°,则∠ADC的度数是( )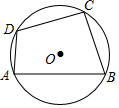 A、70° B、110° C、130° D、140°7. 在一个口袋中有4个完全相同的小球,它们的标号分别为1,2,3,4,从中随机摸出两个小球,则摸出的两个小球标号之和大于4的概率是( )A、 B、 C、 D、8. 把一些书分给几名同学,若________;若每人分11本,则不够.依题意,设有x名同学,可列不等式9x+7<11x,则横线上的信息可以是A、每人分7本,则可多分9个人 B、每人分7本,则剩余9本 C、每人分9本,则剩余7本 D、其中一个人分7本,则其他同学每人可分9本9. 如图, 垂直于 ,P为线段 上的动点,F为 的中点, , , , .若 , ,则 的长约为( )(参考数据: , )
A、70° B、110° C、130° D、140°7. 在一个口袋中有4个完全相同的小球,它们的标号分别为1,2,3,4,从中随机摸出两个小球,则摸出的两个小球标号之和大于4的概率是( )A、 B、 C、 D、8. 把一些书分给几名同学,若________;若每人分11本,则不够.依题意,设有x名同学,可列不等式9x+7<11x,则横线上的信息可以是A、每人分7本,则可多分9个人 B、每人分7本,则剩余9本 C、每人分9本,则剩余7本 D、其中一个人分7本,则其他同学每人可分9本9. 如图, 垂直于 ,P为线段 上的动点,F为 的中点, , , , .若 , ,则 的长约为( )(参考数据: , ) A、1.2 B、 C、 D、10. 某班“数学兴趣小组”探究出了有关函数 (图象如图)的三个结论:①方程 有1个实数根,该方程的根是 ;②如果方程 只有一个实数根,则a的取值范围是 或 ;③如果方程 有2个实数根,则a的取值范围是 或 .你认为正确的结论个数有( )
A、1.2 B、 C、 D、10. 某班“数学兴趣小组”探究出了有关函数 (图象如图)的三个结论:①方程 有1个实数根,该方程的根是 ;②如果方程 只有一个实数根,则a的取值范围是 或 ;③如果方程 有2个实数根,则a的取值范围是 或 .你认为正确的结论个数有( ) A、3 B、2 C、1 D、0
A、3 B、2 C、1 D、0二、填空题
-
11. 因式分解: =.12. 为了考察甲、乙两种小麦的长势,分别从中抽出200株测得其高度,并求得它们的方差分别为 , ,则种小麦的长势比较整齐.13. 如图,平行于y轴的直尺(部分)与反比例函数 的图象交于A,C两点,与x轴交于B,D两点,连结 ,点A,B对应直尺上的刻度分别为5,2,直尺的宽度 , ,则点C的坐标是.
 14. 如图所示的网格是正方形网格,则 (点 、 、 、 、 是网格线交点).
14. 如图所示的网格是正方形网格,则 (点 、 、 、 、 是网格线交点). 15. 如图,这是一个供滑板爱好者使用的U型池的示意图,该U型池可以看成是长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是直径为 的半圆,其边缘 ,点 在 上, ,一滑板爱好者从A点滑到E点,则他滑行的最短距离约为 .(边缘部分的厚度忽略不计)
15. 如图,这是一个供滑板爱好者使用的U型池的示意图,该U型池可以看成是长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是直径为 的半圆,其边缘 ,点 在 上, ,一滑板爱好者从A点滑到E点,则他滑行的最短距离约为 .(边缘部分的厚度忽略不计) 16. 在平行四边形 中, 平分 交 于点F, ,点E是对角线 上的点,连结 .
16. 在平行四边形 中, 平分 交 于点F, ,点E是对角线 上的点,连结 . (1)、如图1,若 ,点G是 的中点,则 .(2)、如图2,以点E为直角顶点,在 的右下方作等腰直角 ,若点E从点A出发,沿 运动到点C停止,设在点E运动过程中, 的中点T经过的路径长为a, 的长为b,则 .
(1)、如图1,若 ,点G是 的中点,则 .(2)、如图2,以点E为直角顶点,在 的右下方作等腰直角 ,若点E从点A出发,沿 运动到点C停止,设在点E运动过程中, 的中点T经过的路径长为a, 的长为b,则 .三、解答题
-
17. 计算: .18. 化简 ,并从1,2,3中选取所有合适的数作为a代入求值.19. 为了解中考英语人机对话日常训练情况,某市从某校九年级学生中随机抽取了部分学生进行了一次英语人机对话测试(把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图,请根据统计图中的信息解答下列问题:
 (1)、本次抽样测试的学生人数是人.(2)、图1中 的度数是 , 请把图2条形统计图补充完整.(3)、今年该市九年级大约有学生20000名,如果全部参加这次中考英语人机对话测试,请估计不及格的人数为多少人.20. 如图,已知二次函数 的图象经过点 ,与x轴交于点A,B,直线 的解析式是 .
(1)、本次抽样测试的学生人数是人.(2)、图1中 的度数是 , 请把图2条形统计图补充完整.(3)、今年该市九年级大约有学生20000名,如果全部参加这次中考英语人机对话测试,请估计不及格的人数为多少人.20. 如图,已知二次函数 的图象经过点 ,与x轴交于点A,B,直线 的解析式是 . (1)、求二次函数图象的顶点坐标.(2)、求不等式 的解.21. 如图所示, 与 相切于点C,线段 交 于点B.过点B作 交 于点D,连结 ,且 交 于点E.若 .
(1)、求二次函数图象的顶点坐标.(2)、求不等式 的解.21. 如图所示, 与 相切于点C,线段 交 于点B.过点B作 交 于点D,连结 ,且 交 于点E.若 . (1)、求 的大小和 的半径长.(2)、求由弦 与弧 所围成的阴影部分的面积(结果保留 ).22. 在疫情期间,某地推出线上名师公益大课堂,为广大师生、其他社会人士提供线上专业知识学习、心理健康疏导.参与学习第一批公益课的人数达到2万人,因该公益课社会反响良好,参与学习第三批公益课的人数达到2.42万人.参与学习第二批、第三批公益课的人数的增长率相同.(1)、求这个增长率;(2)、据大数据统计,参与学习第三批公益课的人数中,师生人数在参与学习第二批公益课的师生人数的基础上增加了80%;但因为已经部分复工,其他社会人士的人数在参与学习第二批公益课的其他社会人士人数的基础上减少了60%.求参与学习第三批公益课的师生人数.23. 如图,四边形 中, ,且满足 ,连结 .
(1)、求 的大小和 的半径长.(2)、求由弦 与弧 所围成的阴影部分的面积(结果保留 ).22. 在疫情期间,某地推出线上名师公益大课堂,为广大师生、其他社会人士提供线上专业知识学习、心理健康疏导.参与学习第一批公益课的人数达到2万人,因该公益课社会反响良好,参与学习第三批公益课的人数达到2.42万人.参与学习第二批、第三批公益课的人数的增长率相同.(1)、求这个增长率;(2)、据大数据统计,参与学习第三批公益课的人数中,师生人数在参与学习第二批公益课的师生人数的基础上增加了80%;但因为已经部分复工,其他社会人士的人数在参与学习第二批公益课的其他社会人士人数的基础上减少了60%.求参与学习第三批公益课的师生人数.23. 如图,四边形 中, ,且满足 ,连结 . (1)、如图1,当 时,求证: .(2)、如图2,若 ,求 的值.(3)、如图3,延长 , 交于点D,连结 ,过点D作 ,若 , .试探究:在射线 上,是否存在点E,使得 的某一个内角等于 的2倍?若存在,连结 ,求 的值;若不存在,请说明理由.24. 已知,二次函数 的图象与x轴相交于点A,B(点A在点B的左侧),与y轴相交于点C.
(1)、如图1,当 时,求证: .(2)、如图2,若 ,求 的值.(3)、如图3,延长 , 交于点D,连结 ,过点D作 ,若 , .试探究:在射线 上,是否存在点E,使得 的某一个内角等于 的2倍?若存在,连结 ,求 的值;若不存在,请说明理由.24. 已知,二次函数 的图象与x轴相交于点A,B(点A在点B的左侧),与y轴相交于点C.
 (1)、若 ,如图1,已知A,C两点的坐标为 .
(1)、若 ,如图1,已知A,C两点的坐标为 .①求抛物线的解析式,并求出B的坐标.
②点P是抛物线上第一象限内一个动点.y轴上有一点 ,连结 交 于点H,若H恰好平分 ,求点P的坐标.
(2)、若 , , , ,如图2,抛物线与一次函数 的图象交于E,F两点,点E在点F的左侧.在直线 上是否存在唯一一点Q,使得 ?若存在,请求出此时k的值;若不存在,请说明理由.