四川省巴中市平昌县2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-03-30 类型:期末考试
一、单选题
-
1. 下列各式中,与是同类二次根式的是( )A、 B、 C、 D、2. 下列方程中是一元二次方程的是( )A、2x+1=0 B、y2+x=1 C、x2+1=0 D、3. 一元二次方程 经过配方后,可变形为( )A、 B、 C、 D、4. 下列四幅图中,能表示两棵树在同一时刻太阳光下的影子的图是( )A、
 B、
B、 C、
C、 D、
D、 5. 在“红桃5、红桃7、红桃9”这三张扑克牌中任取一张,抽到“红桃7”的概率是( )A、 B、 C、 D、16. 如图,∠1=∠2,则下列各式不能说明△ABC∽△ADE的是( )
5. 在“红桃5、红桃7、红桃9”这三张扑克牌中任取一张,抽到“红桃7”的概率是( )A、 B、 C、 D、16. 如图,∠1=∠2,则下列各式不能说明△ABC∽△ADE的是( )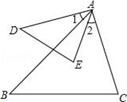 A、∠D=∠B B、∠E=∠C C、 D、7. 如图,直线 ,直线 和 被 , , 所截, , , ,则 的长为( )
A、∠D=∠B B、∠E=∠C C、 D、7. 如图,直线 ,直线 和 被 , , 所截, , , ,则 的长为( )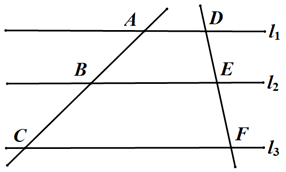 A、2 B、3 C、4 D、8. 如图,面积为S的菱形ABCD中,点O为对角线的交点,点E是线段BC单位中点,过点E作EF⊥BD于F,EG⊥AC与G,则四边形EFOG的面积为( )
A、2 B、3 C、4 D、8. 如图,面积为S的菱形ABCD中,点O为对角线的交点,点E是线段BC单位中点,过点E作EF⊥BD于F,EG⊥AC与G,则四边形EFOG的面积为( )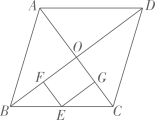 A、 B、 C、 D、9. 如图,点A,B,C在正方形网格的格点上,则sin∠BAC=( )
A、 B、 C、 D、9. 如图,点A,B,C在正方形网格的格点上,则sin∠BAC=( )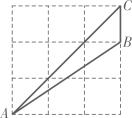 A、 B、 C、 D、10. 一人携带变异新冠状病毒,经过两轮传染后共有 人感染,设每轮传染中平均一个人传染了 个人,则可列方程( )A、 B、 C、 D、11. 设关于x的方程 的两个实数根为 、 ,现给出三个结论:① ;② ;③ 则正确结论的个数是( )A、 B、 C、 D、无法确定12. 构建几何图形解决代数问题是“数形结合”思想的重要性,在计算tan15°时,如图.在Rt△ACB中,∠C=90°,∠ABC=30°,延长CB使BD=AB , 连接AD , 得∠D=15°,所以tan15° .类比这种方法,计算tan22.5°的值为( )
A、 B、 C、 D、10. 一人携带变异新冠状病毒,经过两轮传染后共有 人感染,设每轮传染中平均一个人传染了 个人,则可列方程( )A、 B、 C、 D、11. 设关于x的方程 的两个实数根为 、 ,现给出三个结论:① ;② ;③ 则正确结论的个数是( )A、 B、 C、 D、无法确定12. 构建几何图形解决代数问题是“数形结合”思想的重要性,在计算tan15°时,如图.在Rt△ACB中,∠C=90°,∠ABC=30°,延长CB使BD=AB , 连接AD , 得∠D=15°,所以tan15° .类比这种方法,计算tan22.5°的值为( ) A、 B、 ﹣1 C、 D、
A、 B、 ﹣1 C、 D、二、填空题
-
13. 如果从1,2,3,4,5,6,7,8,9,10这10个数中任意选取一个数,那么取到的数恰好是5的倍数的概率是 .14. 若x<2,化简 的正确结果是.15. 计算: .16. 若 ,则 .17. 如图,小明在A时测得某树的影长为2m,B时又测得该树的影长为8m,若两次日照的光线互相垂直,则树的高度为m.
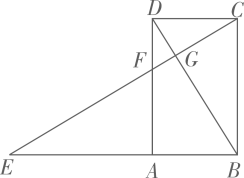
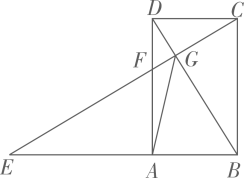
 18. 如图,在 中, ,点D是 的中点,连结 ,过点B作 ,分别交 于点 ,与过点A且垂直于 的直线相交于点G,连结 ,给出以下几个结论:① ;② ;③点F是 的中点;④ .其中正确的结论是(写出所有正确结论的序号).
18. 如图,在 中, ,点D是 的中点,连结 ,过点B作 ,分别交 于点 ,与过点A且垂直于 的直线相交于点G,连结 ,给出以下几个结论:① ;② ;③点F是 的中点;④ .其中正确的结论是(写出所有正确结论的序号).
三、解答题
-
19.(1)、计算:(2)、解方程:(3)、先化简,再求值: ,其中20. 已知: 在平面直角坐标平面内,三个顶点的坐标分别为 、 、 (正方形网格中每个小正方形的边长是一个单位长度).
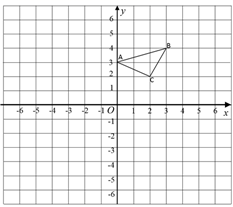
( 1 )画出 向下平移4个单位长度得到的 ,并写出点 的坐标;
( 2 )以点B为位似中心,在网格内画出 ,使 与 位似,且位似比为 ,并写出点 的坐标;
( 3 ) 的面积是多少个平方单位?
21. 已知 , 是一元二次方程 的两个实数根.(1)、求k的取值范围;(2)、是否存在实数k,使得等式 成立?如果存在,请求出k的值,如果不存在,请说明理由.22. 经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转.如果这三种可能性大小相同,现有两辆汽车经过这个十字路口.(1)、试用树形图或列表法中的一种列举出这两辆汽车行驶方向所有可能的结果;(2)、求至少有一辆汽车向左转的概率.23. 某校为检测师生体温,在校门安装了某型号测温门.如图为该测温门截面示意图,已知测温门AD的顶部A处距地面高为2.2m,为了解自己的有效测温区间.身高1.6m的小聪做了如下实验:当他在地面N处时测温门开始显示额头温度,此时在额头B处测得A的仰角为18°;在地面M处时,测温门停止显示额头温度,此时在额头C处测得A的仰角为60°.求小聪在地面的有效测温区间MN的长度.(额头到地面的距离以身高计,计算精确到0.1m,sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)